数据结构-数组和广义表

一、数组的顺序表现和实现

主要有两种存储方式：

• 以行序为主
• 以列序为主

 二、矩阵的压缩存储

1.特殊矩阵--下（上）三角矩阵

可以定义一个长度为的一维数组来存储

如：下三角i>=j：a[i][j]对应存储在sa[i*(i-1)/2+j-1]

2.稀疏矩阵

用三元顺序表存储，三元组分别记录非零元素的行、列位置和元素值

（1）三元组顺序表的实现

#define MAXSIZE 100
typedef struct {
    int i,j;//行下标和列下标
    ElemType e;
}Triple;
typedef struct{
    Triple data[MAXSIZE+1];//data[0]空出来
    int mu,nu,tu;//矩阵的行数、列数、非零元素的个数
}TSMatrix;

（2）三元顺序表的转置实现

• 原三元表的col相当于转置后的行，将col作为最外面的循环计数条件，是依次把转置后的每一行（也就是原三元表中列数为现在的行数的）非零元素都遍历找到；
• q为转置后data数组的下标，每添加一个就自增1；
• 第二层循环是在原三元组中找到列数即j和此次col匹配的非零元素。

Status TransposeSMatrix(TSMatrix M,TSMatrix &T){
    int col,p,q;
    T.mu=M.nu;
    T.nu=M.mu;
    T.tu=M.tu;
    if(T.tu){//T不全为0即非零元素个数不等于0
    q=1;
    for(col=1;col<=T.mu;col++){
        for(p=1;p<=M.tu;p++){
            if(M.data[p].j==col){
                T.data[q].i=M.data[p].j;
                T.data[q].j=M.data[p].i;
                T.data[q].e=M.data[p].e;
                q++;
            }
        }
    }
    }
    return OK;
}
                

*时间复杂度为：O(M.nu*M.tu)

三、广义表的类型定义

1.广义表的术语：

表头（Head）：非空广义表的第一个元素

表尾（Tail）：除了表头的其余元素组成的表

深度：广义表中括号嵌套的最大层数

原子：如果ai是单个元素则称为元素，一般用小写字母表示

子表：如果ai是广义表则称为子表，一般用大写字母表示

长度：直观上有几个元素，嵌套之类的也只看做一个元素

 

 2.广义表的存储结构

typedef enum(ATOM,LIST}ElemTag;
typedef struct GLNode{
    ElemTage tag;
    union{
    AtomType atom;
    struct {struct *hp,*tp;}ptr;
    }
}*Glist;

 

 

---

1.

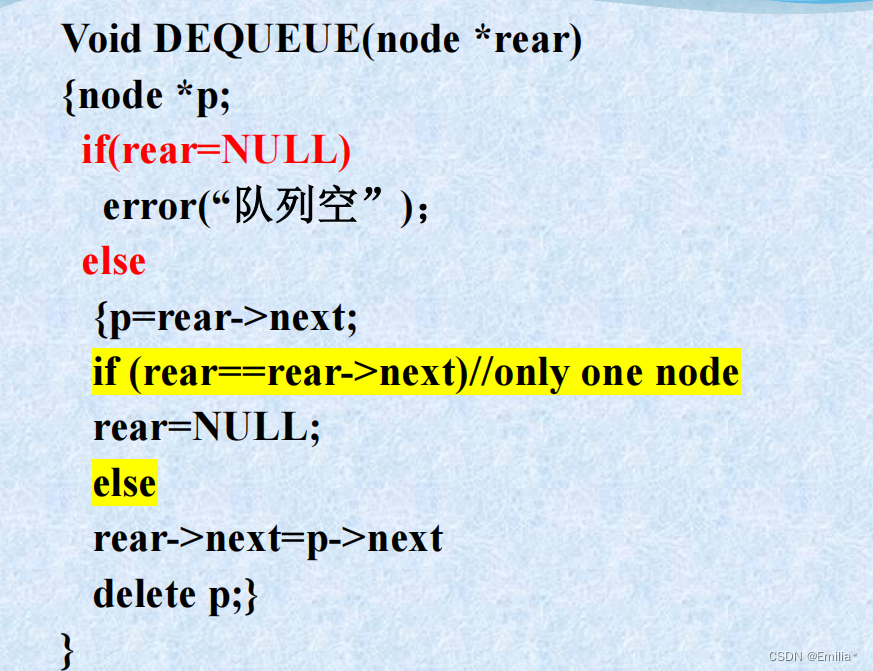
2.注意入队时队列为空的情况；出队时仅有一个元素的情况