数据库设计（概念、逻辑、物理）

数据库设计概述与需求分析：

 

结构设计： 概念结构、逻辑结构、物理结构。

行为设计：功能模型、事务设计、应用设计。

 

 

 

 

 

 

 

 

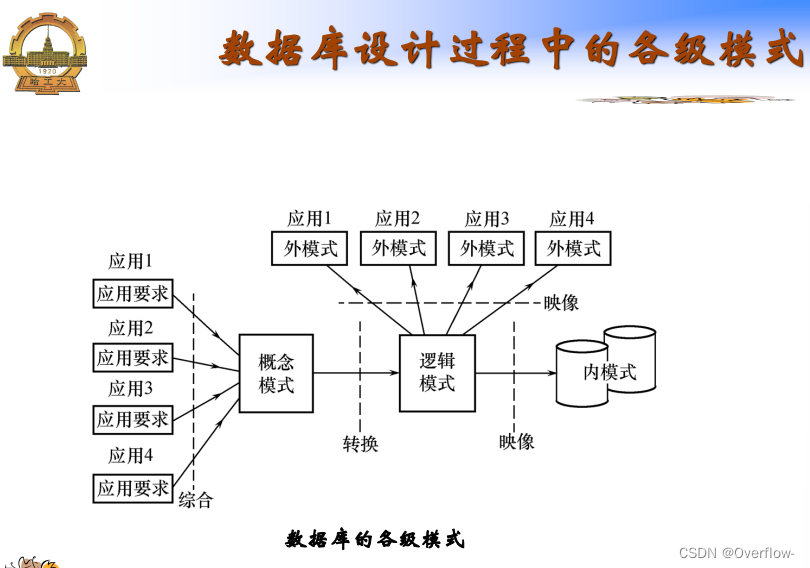
信息要求、处理要求、安全性与完整性要求。

 

 

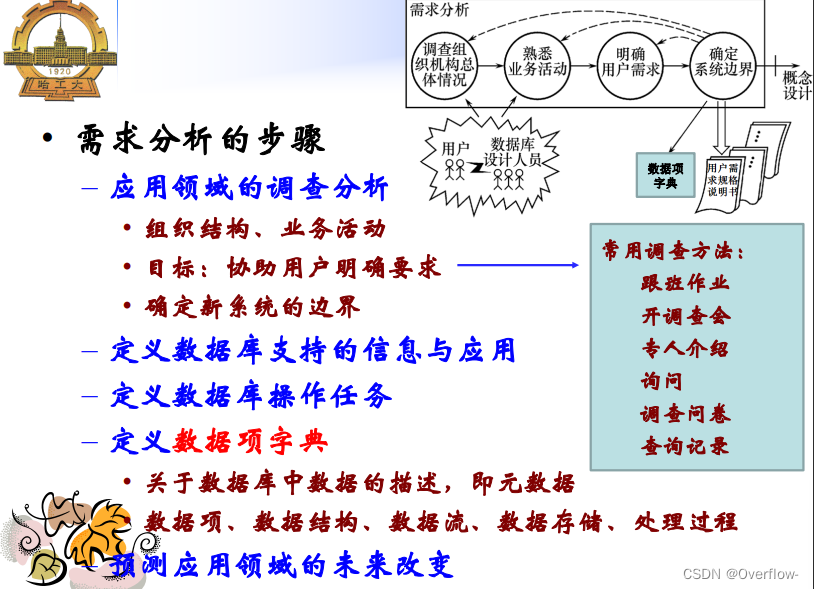
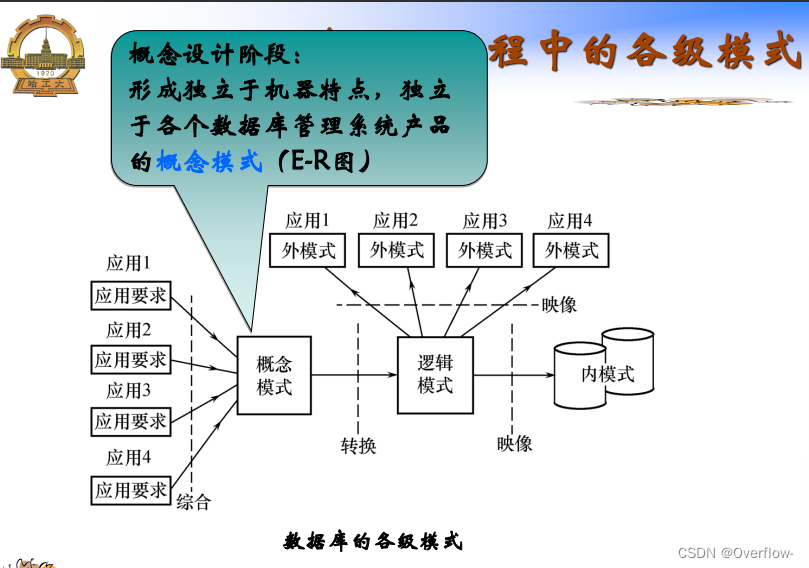
概念数据库设计:

 

 

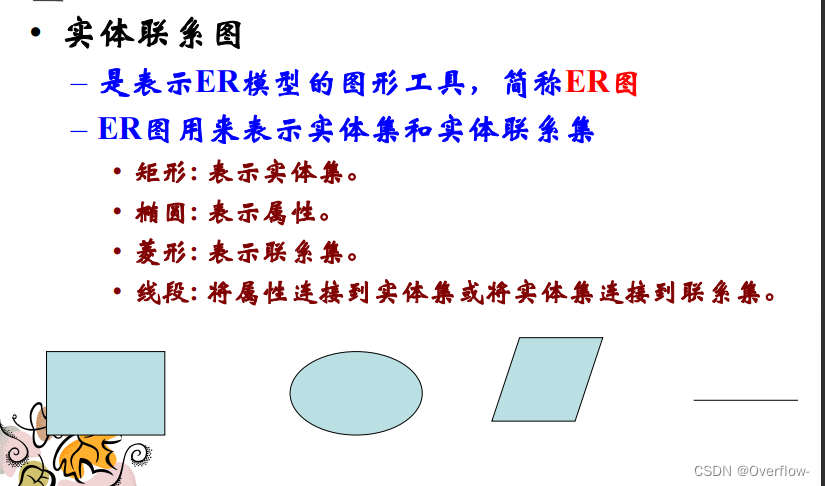
 实体联系模型：

 实体-属性-联系

 

 实体集是相同类型（即具有相同性质或属性）的实体集合。

实体集不必互不相交。

 

 属性是实体集映射到域的函数。具体包括单值/多值属性、简单/复合属性、导出属性。

 

 

 

 

 联系集即为同类联系的集合。

 实体之间的联系既可以使用联系集定义，也可以通过实体属性来表示。

 

 参与约束：部分参与——全部参与。

 联系集的属性：描述性属性

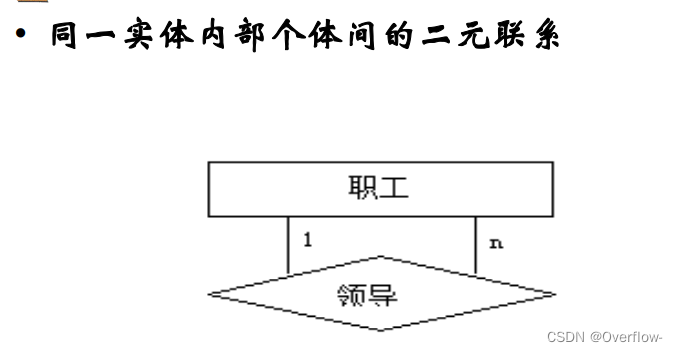
 一个主实体对应的多个弱实体之间可以相互区别。

 

 弱实体必须具有一个或多个属性，使得这些属性可以与主实体集的主码相结合形成相应弱实体集的主码，这样的弱实体属性称为弱实体集的部分码。

 

 

 

 

 

 

 

 

 

 

 

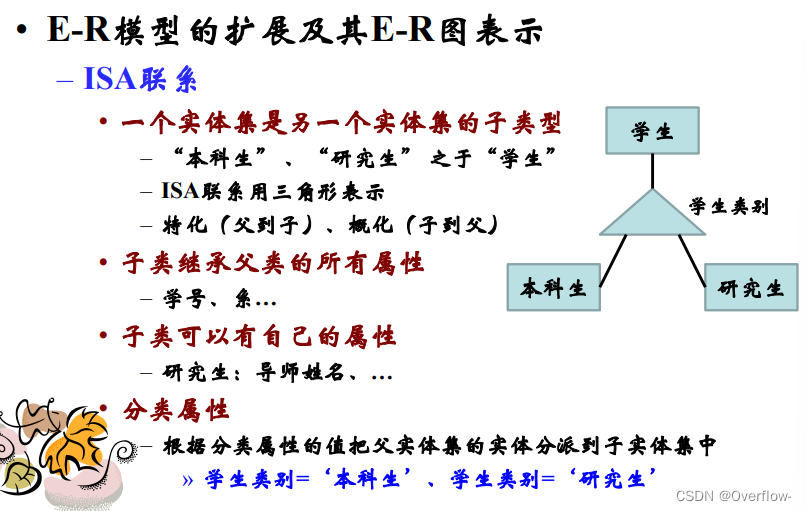
 ISA联系 子类继承父类的所有属性；子类可以拥有自己的属性；联系中具有分类属性。

 不相交约束——可重叠约束。

 完备性约束：完全特化——部分特化。

 

根据min来约束是否强制。

 

 

 

 项目与指导记录一对多 学生导师亦然，但是无法描述项目、学生与导师的多对一关系。

 

 

 概念数据库设计的基本步骤：

 

 

 集中式设计方法——视图综合分析法

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

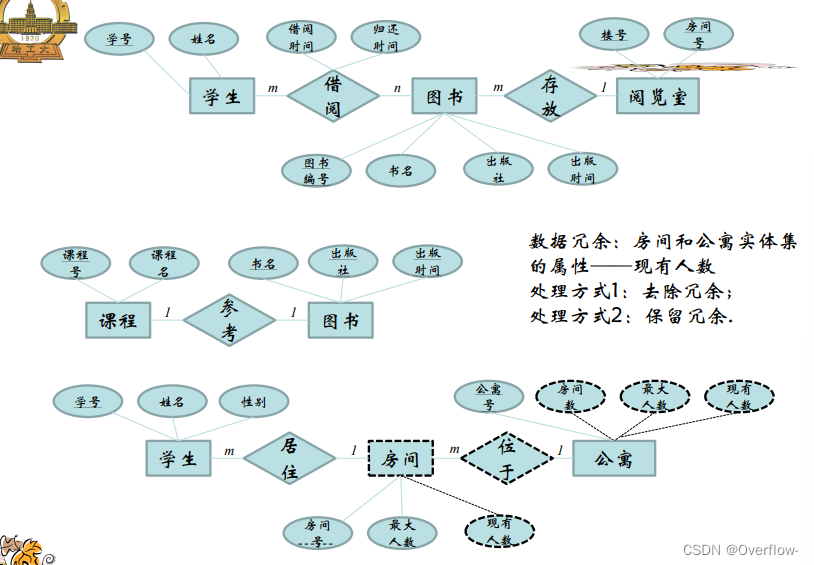
 课程参考的是抽象的图书，可以说是这本书的概念；学生在图书馆里借阅的是真实存在的纸质书，给它们直接合并是不行的，假设映射基数填课程-1-参考-m-图书，一门课程规定了只能参考一种书，这个m只能当m本书来理解，但是又引出了逻辑谬误：参考的是m本一样的书？其实参考的只是“这本书”罢了。将m换成1也是一样的，不能把实体书和概念书混淆。

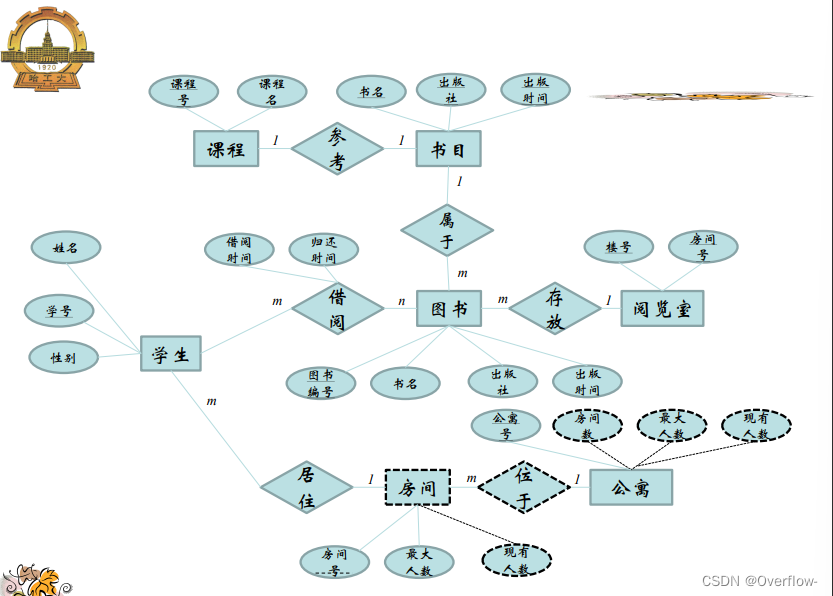
 事务的设计：

逻辑数据库设计：

 

 形成初始关系数据库模式：

 

 

 

 S包含E的所有简单属性和E的复合属性的简单子属性。（复合属性本身被去掉了）

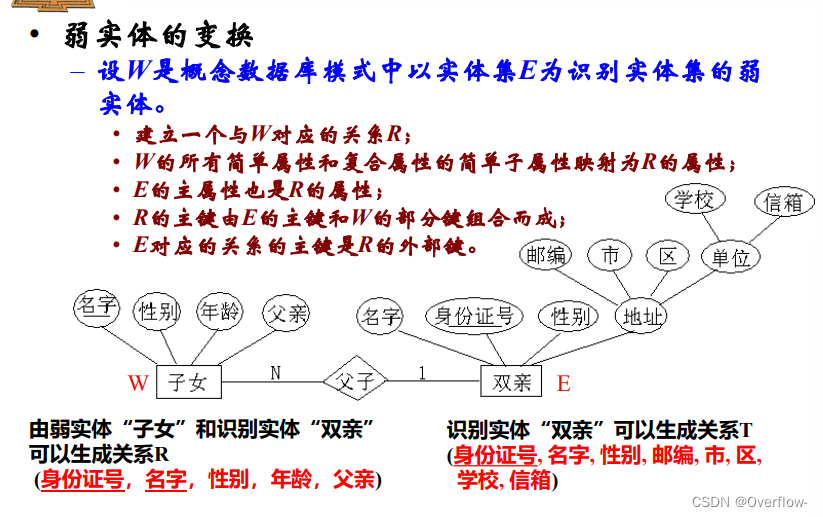
 将弱实体W（E是它的识别实体集）变换为关系

R包含W的所有简单属性与复杂属性的简单子属性；E的主键与W的部分码组合成为W的主键，E是W参照E的外键。

 为每一个多值属性都建立一个新的关系去表示它。

新生成关系的主键是原关系的主键和多值属性/其简单子属性。

 使用属性表示联系。

1.T的主键作为外键派入S（或反之）；联系R的简单属性和复合属性的简单子属性作为简单属性派入S或T。

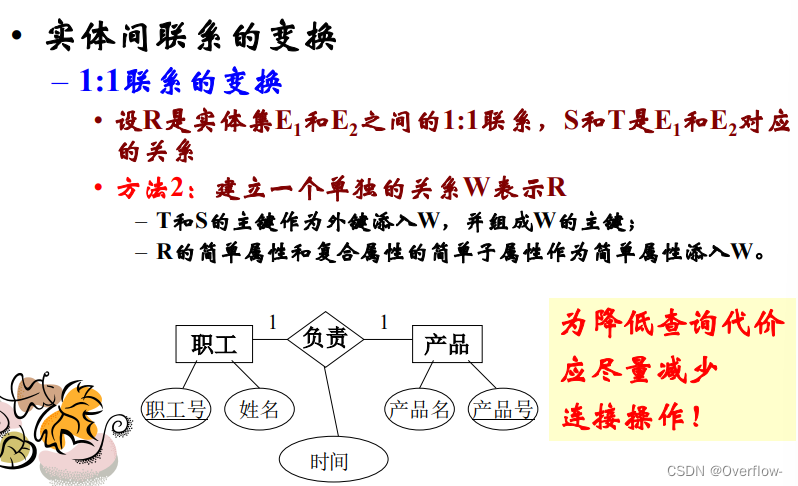
 2.在1：1联系转化为关系模式的时候，E1实体转换为关系T，E2实体转换为关系S。对于E1和E2之间的1：1联系R，为R建立关系W，W中需要包含T的主键和S的主键，并用T的主键或者S的主键作为W的主键，不是用T的主键和S的主键联合组成W的主键。PPT有误。

 1.不建立新关系，由于是1：n的联系，T的每个实体至多与S的一个实体对应，用T表示R。

S的主键作为外键添入T，联系R的简单属性和复合属性的简单子属性作为简单属性派入S或T。

2. 在1：n联系转化为关系模式的时候，E1实体转换为关系T，E2实体转换为关系S。对于E1和E2之间的1：n联系R，为R建立关系W，W中需要包含T的主键和S的主键，并用E2的主键作为所属关系的主键,R的特定属性作为简单属性放入W。

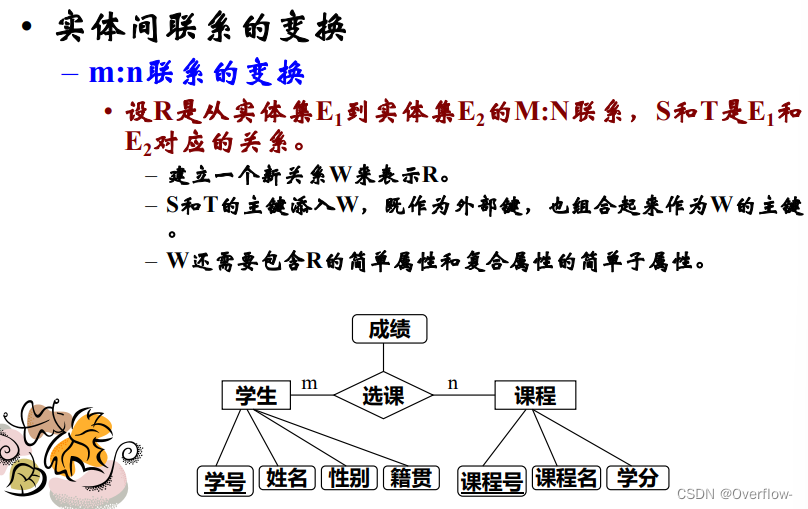
S和T的主键派入W，既作为外部键也组合起来作为W的主键。

 

 

 

 ISA不相交且完全时，2少存储一次所有学生的学号；并且同时查询学生和本科生/研究生的属性时无需join操作。

ISA有重叠时学生主体的属性重复存储在本科生和研究生关系中；无法定义参照“学号”属性的主外键约束（其他实体可能与学生实体之间存在联系）。

 

 

 

 

 

 

 

 

 

 

 易证互相函数决定推一对一联系。

 

 全键。

 

 函数依赖的公理系统：

 

 

自反律：由平凡函数依赖推得；

 增广律，笛卡尔积不影响依赖的方向；

传递。

 

 

 

 F的闭包是函数依赖的集合；X关于F的闭包是属性的集合。

 

 

 

 S2中W涉及F中的所有右部属性，每次遍历找到当前X中所有元素所决定的右部元素并且加入闭包X直到X不再改变抑或X等于U。

 这里为什么要算A，B决定的属性呢？很简单，自反律得到。

 

 

 

 

 

 

 采用循环证明。

 L类和N类推不出来。R类必能推出来且不参与推导的过程，所以不在候选键中。

 

 

 从LR里找。

 

 

 极小函数依赖集：右部最小（仅有一个属性）；左部最小（不存在真子集进行替换）；整体最小（不能删减函数依赖）。

 

 

 

 

 

 

消除了非键属性对键属性的部分函数依赖。

 

 插入异常：确定了一个系的住处但是无法存储。

删除异常：学生毕业了，然而系和住处的对应关系也随之删除。

http://t.csdn.cn/aEPkT

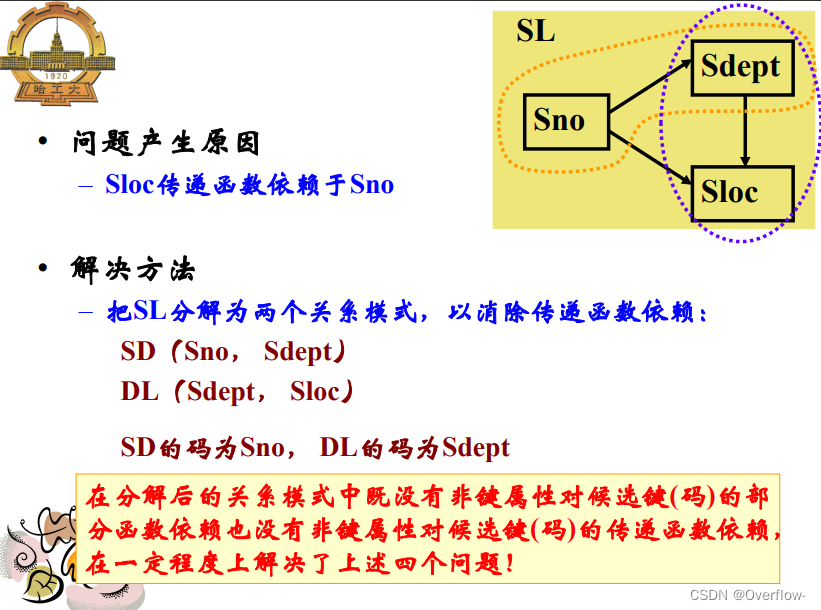
 若R∈3NF，则R的每一个非键属性既不部分函数 依赖于候选键也不传递函数依赖于候选键。

 

 

 

 

 没有任何属性对候选键的部分函数依赖和传递函数依赖。

 

 想满足BCNF，就必须保证没有任何属性对候选键的部分函数依赖和传递函数依赖，由这个定义可知传递函数依赖必不可能；如果满足部分函数依赖的话就违背了候选键的定义，可知亦不可能。

 也就是说每一个左部都是候选键才行。

 所有非键属性都完全函数依赖于每个候选键；所有键属性都完全函数依赖于每个不包含它的候选键；没有任何属性完全函数依赖于非码的一组属性。

 

 

 

 

 将函数依赖闭包中属于这个属性集合Ui的依赖拿出来做个集合，为什么还要取一个覆盖呢？也就是它存在等价形式，它的所有等价形式都是F在Ui上的投影。

 

 

 

 关系模式分解优先考虑：分解的无损连接性；函数依赖的保持性。

 

 

 由于属性间函数依赖的关系，重新连接回去可能会导致元组变多，也是一种信息丢失。

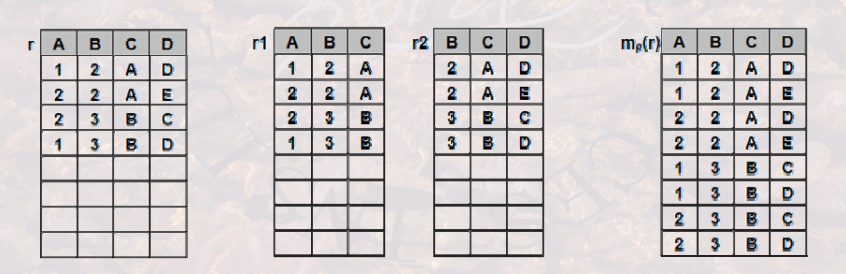
分成几个表后做自然连接，在内容上与原来的表内容是否等价：分解的无损连接性

  像上表就不符合内容等价性，r被分解成r1和r2,自然连接以后成，容易看出该表与原来r的表增加了几行数据，这些增加的数据有可能是错的，因此数据内容上不等价。 

 

 

 

 

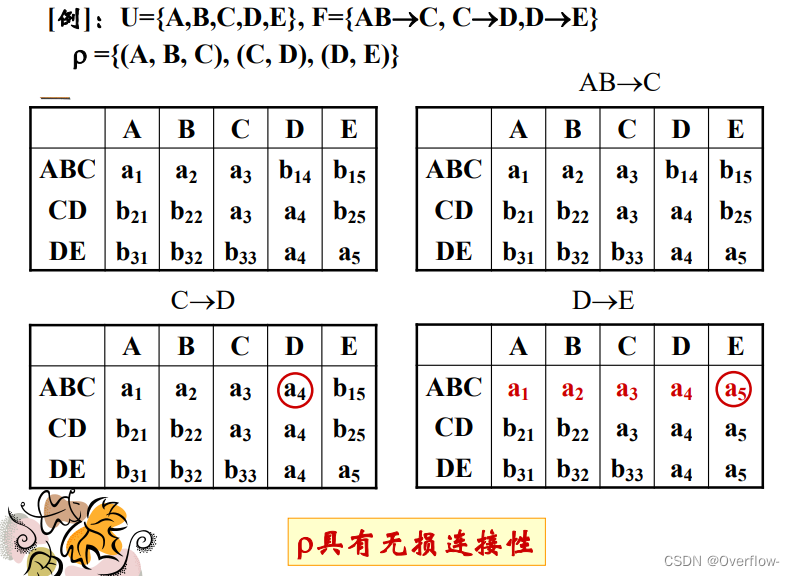
 （也就是说等价的）

 

 

 

利用了最小函数依赖集的性质！神！

 

 

 

计算属性集的闭包和验证无损连接性的过程差不多。

 

 那么，计算极小函数依赖集的闭包就可以拿来做无损连接性的验证。

 

 

 

 显然，CTB为全键且满足BCNF。

 

 

 

 

 

 

 

 

 

 关系模式优化：

 

 

 

 垂直分解必须不损失关系模式的语义（保持无损连接性和函数依赖）

 

 定义关系上的完整性和安全性约束：

 

 http://t.csdn.cn/NCIvR

 子模式定义：

 

 性能估计：

 

 物理数据库设计：

 

关系上定义的索引数并不是越多越好，系统为维护索引要付出代价，查找索引也要付出代价。