堆的概念，和代码解析以及堆的价值（一）

二叉树可以用链式存储，也可以用顺序存储，该篇主要是顺序存储

一.堆的概念

堆是一种完全二叉树（前n-1层是满的，最后一层可以不满，但是从左到右必须是连续的)

二.堆的性质

大堆：树中所有父亲都大于等于孩子

小堆:树中所有父亲都小于等于孩子

三.堆的逻辑结构和物理结构

逻辑结构图片如下:

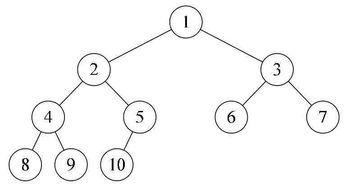
逻辑结构:便于理解，想象出来的

物理结构：实实在在在内存中是如何存储的（堆实际上是存储在数组中的）

1. • 数组是如何存储二叉树的？

一层一层存，并且孩子和父亲下标的关系：

leftchild= parent*2+1 rightchild = parent*2+2 parent = (child-1)/2

1. 任何一个数组都可以看作完全二叉树，但不一定是堆

四.代码

1.动态数组存储堆

2.三个基本函数

3.插入数据会影响到它的祖先

4.向上调整步骤

在当前位置插入数据，找到它的父亲，（大堆）如果父亲比孩子小，则交换，再将父亲的下标赋给孩子，由当前位置孩子的下标再找到父亲，比较大小，进行循环，直到孩子下标小于等于0

因为它是一个个插入的，如果满足条件就可以直接跳出，不需要考虑再往上几层是否满足大堆的条件

4.插入堆(HeapPush)的时间复杂度

扩容可以忽略，向上调整最少不需要调整0(1),最大调整高度次0(logN) (系数可以省略）

a.高度和结点个数关系：

满二叉树第k层：2^(k-1)

高度为h满二叉树总结点:2^h-1

假设满二叉树有N个结点：N = 2^(h-1) h = log2(N+1)

完全二叉树:

最多:2^k-1

最少：2^0+2^1+2^2+……+2^(k-1)+1 = 2^(k-1)-1+1 = 2^(k-1)

N = 2^(k-1) k = log2N+1

5.打印堆

五.堆的价值

1. • 排序（下一篇）

2. • topK问题

大堆能保证根是堆里面最大的数

思路:最后子孙和根进行交换，原因:方便删除，顺序表尾删很方便，如果挪动覆盖效率太慢

优点：左子树和右子树依然是大堆

挑选左孩子和右孩子大的一个和根比较（挑一个能坐稳这个位置的人），若根比大的那个孩子小，就交换，这个孩子的下标赋给根，再进行比较，直到左孩子的下标大于等于总结点

HeapPop和HeapTop是两个配合的接口

最牛逼的地方在哪？

选数的过程相当得快

向上调整建堆的时间复杂度为n*o(logn)

HeapPop的时间复杂度为：向下调整，最多调整高度，为o(logn)

logn极快，1000个数logn只需要10次 1000000只需要20次 10亿只需要向下调整30次

六.打印排序