JAVASE语法零基础——方法的使用

Java系列文章目录

---

Write once,Runanywhere.🔥🔥🔥

本派文章讲解java里的方法，在学习时，如果你感觉对方法一词感觉很陌生，那你可以先将方法理解成C语言里的函数，这样便于你快速学习java中的方法。下一篇文章会讲一些递归的练习题以及递归当中追经典的青蛙跳台阶和汉诺塔问题。

💥 💥 💥如果你觉得我的文章有帮助到你，还请【关注➕点赞➕收藏】，得到你们支持就是我最大的动力!!!
💥 💥 💥

⚡版权声明：本文由【马上回来了】原创、在优快云首发、需要转载请联系博主。
版权声明：本文为优快云博主「马上回来了」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

🚀🚀🚀 新的知识开始喽🚀🚀🚀

---

---

1.方法的定义以及使用

1.1方法的概念

方法就是一个代码片段，类似于C语言里的函数。方法存在的意义：
1.使代码模块化，提高代码的可读性。
2.只写一次，多次调用，提高效率

1.2 .方法的定义

方法语法格式

 //方法定义
> 修饰符 返回值类型 方法名称(参数列表)｛
> 方法体代码;
> return 返回值;
> ｝

示例：实现一个判断素数的方法

public static boolean isPrime(int n){
        for (int i = 2; i < Math.sqrt(n) ; i++) {
            if(n%i == 0){
                return false;
            }
        }
        return true;
    }

注意事项

• 修饰符：现阶段直接使用public static固定搭配
• 返回值类型：如果方法有返回值，返回值类型必须要与返回的实体类型一致，如果没有返回值，必须写成void
• 方法名：采用小驼峰(首字母小写)
• 参数列表：如果方法没有参数，()什么都不写；如果有参数，需指定参数类型，多个参数之间使用逗号隔开
• 方法体：方法内部要执行的语句
• 在java当中，方法必须写在类当中
• 在java当中，方法不能嵌套定义
• 在java当中，不需要进行方法声明

1.3 方法的调用和执行过程

方法的调用过程与执行过程

方法的执行就好比一个工厂：

注意事项

• 定义方法的时候，不会执行方法的代码，只有调用的时候才会执行
• 一个方法可以被多次调用
  示例：计算 1！+ 2！+ 3！+4！+5！

 public static void main(String[] args) {
        int sum = 0;
        for(int i = 1; i <= 5; i++){
            sum += fac(i);//
        }
        System.out.println("sum = "+sum);
    }
    //求阶乘的方法
    public static int fac(int n){
        System.out.println("计算n的阶乘中n!="+n);
        int ret  = 1;
        for (int i = 1; i <= n ; i++) {
            ret*=i;
        }
        return ret;
    }

如果不使用方法，又想避免二次循环，代码可以这样写：

public static void main(String[] args) {
        int sum = 0;
        int ret = 1;
        for (int i = 1; i <= 5 ; i++) {
            ret*=i;
            sum+=ret;//将得到的每个累乘叠加
        }
        System.out.println(sum);
    }

2.方法的传参

在java中，实参的值永远都收拷贝到形参中的，不存在得到基本变量的地址，形参和实参本质是两个实体。
看代码：

public static void main(String[] args) {
        int a = 10;
        int b = 20;
        swap(a,b);
        System.out.println("交换前");
        System.out.println(a+" "+b);
        System.out.println("交换后");
        System.out.println(a+" "+b);
    }
    public static void swap(int x, int y){
        int tmp = x;
        x = y;
        y = tmp;
        System.out.println("交换前");
        System.out.println(x+" "+y);
        System.out.println("交换后");
        System.out.println(x+" "+y);
    }

运行结果：

原因：

3 方法重载

要实现方法重载，必须注意以下三点：
1.方法名称相同
2.形参列表不同
3.返回值是否相同不做要求，可以一样，也可以不一样。
方法重载使得我们在进行大量代码书写时，使得方法名更加简洁。看下面代码：
示例：实现不同类型的加法，方法名都是add，代码更加简洁

    public static int add (int x,int y){
        return x+y;
    }
    public static double add(double x,double y){
        return x+y;
    }
    public static int add(int x,int y,int z){
        return x+y+x;
    }

编译器在编译代码时，会对实参类型进行推演，根据推演的结果来确定调用哪个方法：

这里重点看下面两块代码：

4 方法签名

你是否会感到困惑：为什么类中的方法名居然可以使用相同的标识符做方法名，
方法签名会给出你答案。方法签名：经过编译器修改之后方法最终的名字。具体方式：方法全路径名+参数列表+返回值类型，构成方法完整的名字。
下面演示一下如何查看方法的签名，就用上面add方法来演示：

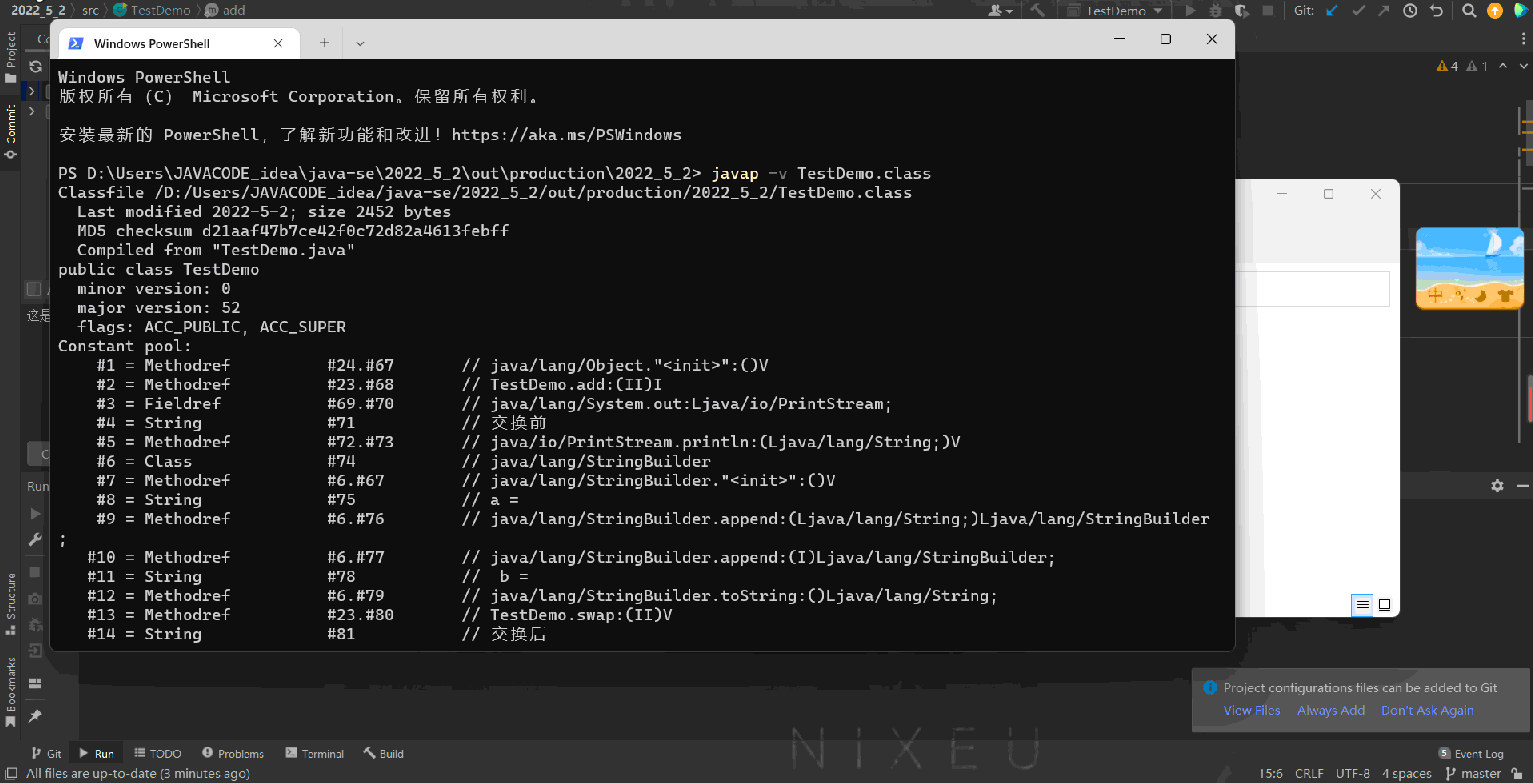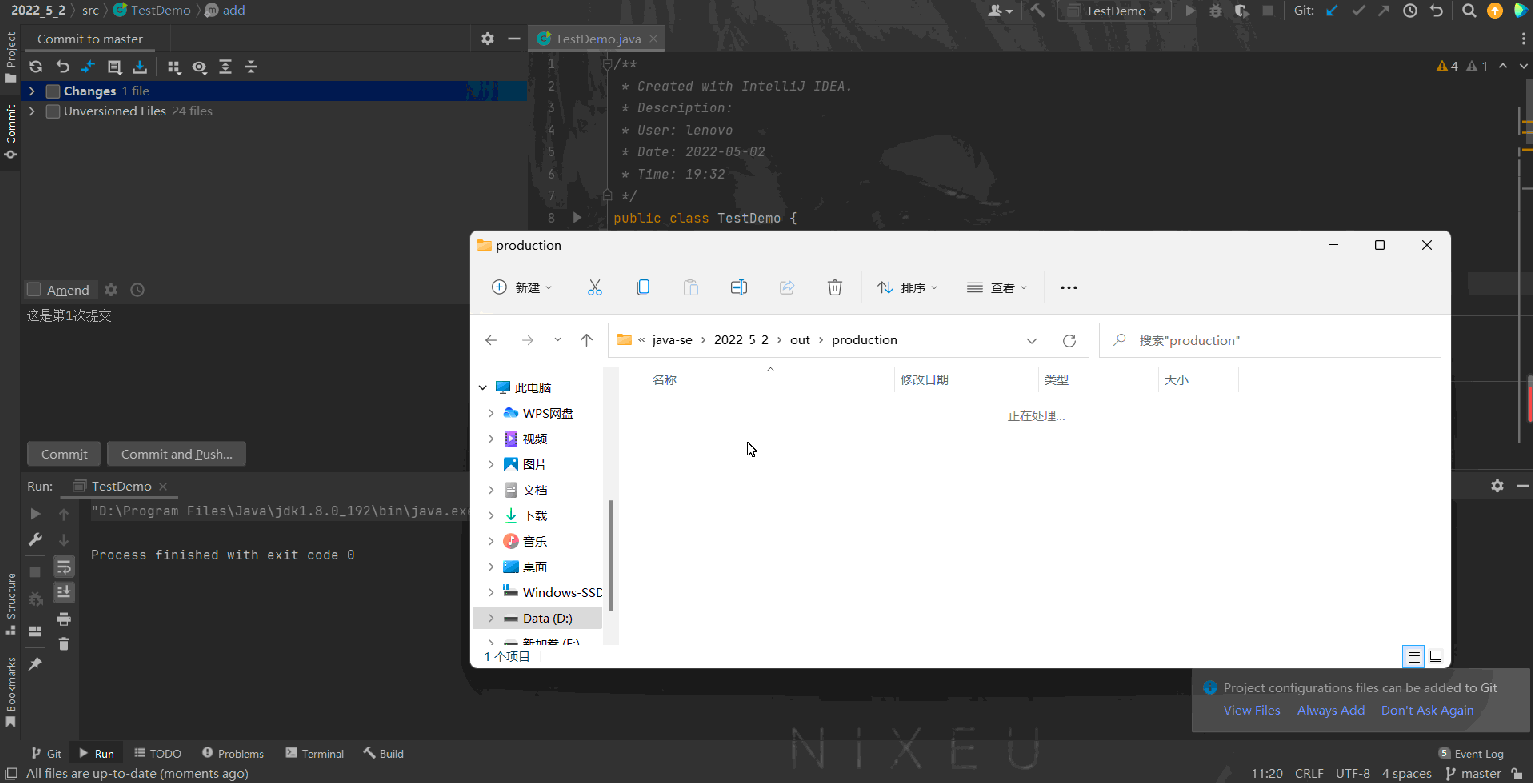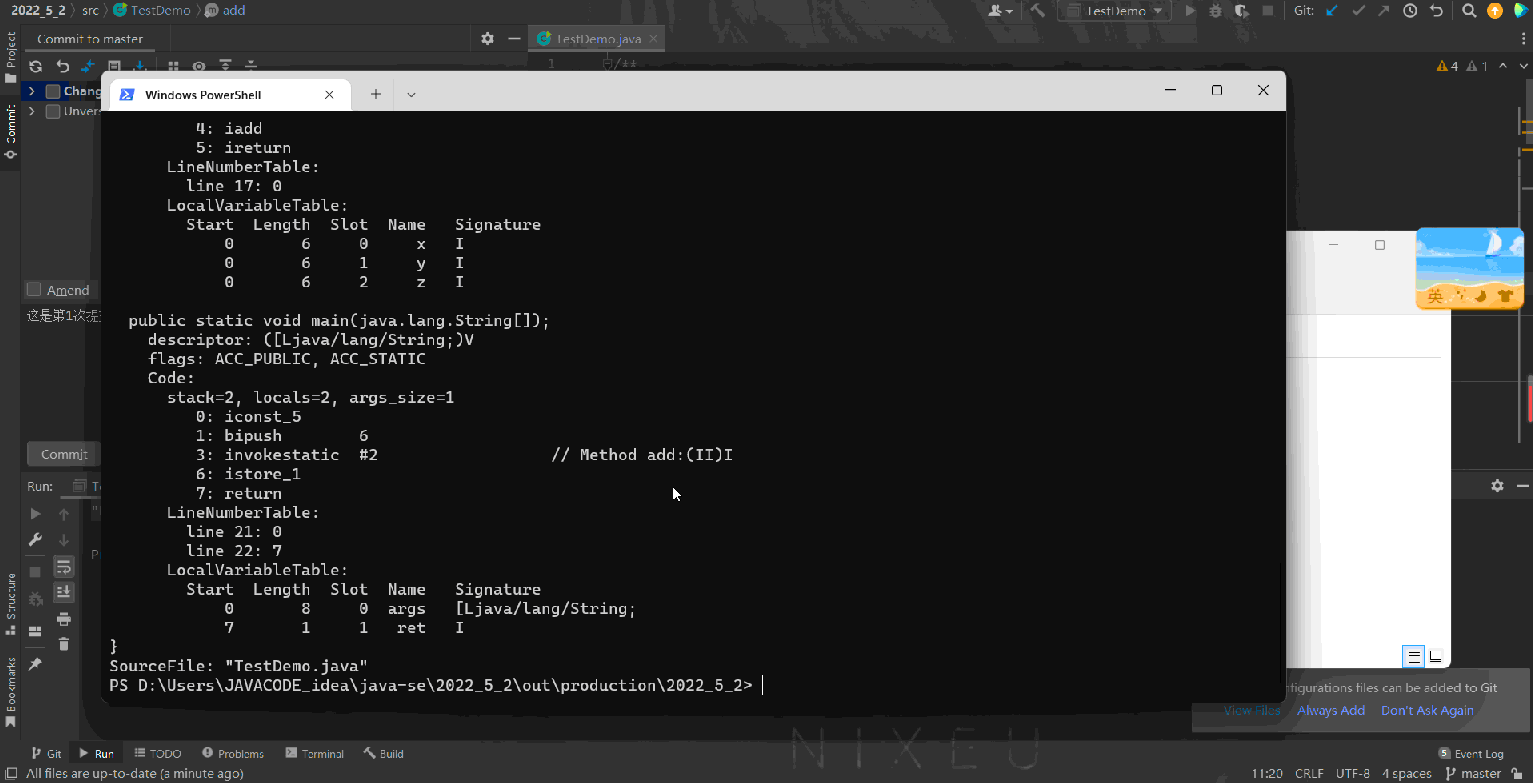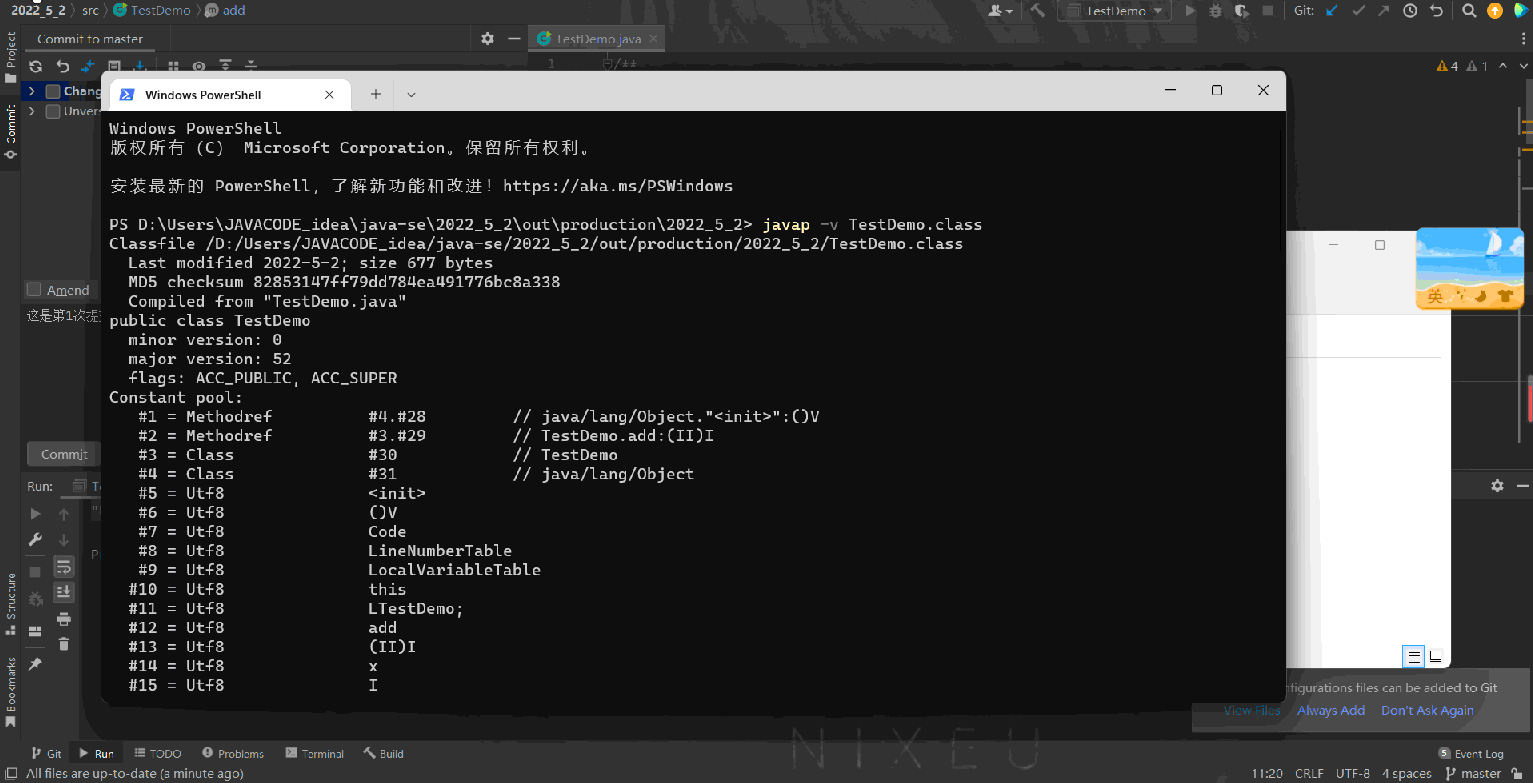
上述代码经过编译之后，然后使用JDK自带的javap反汇编工具查看，具体操作：

1. 先对工程进行编译生成.class字节码文件
2. 在控制台中进入到要查看的.class所在的目录
3. 输入：javap -v 字节码文件名字即可
   方法签名中的一些特殊符号说明：

特殊字符	数据类型
V	void
Z	boolean
B	byte
C	char
S	short
I	int
J	long
F	float
D	double
[	数组(以[ 开头，配合其他的特殊字符，表示对应数据类型的数组，几个[ 表示几维数组)
L	引用类型，以L开头，以;结尾，中间是引用类型的全类名

5 递归

一个方法在执行过程中调用自己，就称为递归。
递归相当于数学上的数学归纳法，有一个起始条件，然后有一个递推公式。

例如, 我们求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)

递归的必要条件：
1.将原来问题划分成其子问题—>大事化小—>递推公式
2.递归出口—>起始条件

递归并不是一个简单东西，首先虽然递归的代码看起来简单，但是可读性并不高，想要掌握递归，除了掌握两个递归的必要的条件以外，还得知道：在执行递归时，代码都是运行到方法调用本身时，就不在继续往主方法下方执行，而是先去继续调用本身，这个过程称为“递”，在其实条件执行结束后，再一次回归到未执行完的代码下方继续执行，这个过程称之为“归”。

下面举两个代码示例：
示例1：有返回值类型的递归—>求5的阶乘
递归思想：5！=54！=543！=5432！=54321

 public static void main(String[] args) {
        int n = 5;
        int ret = Fac(n);
        System.out.println(ret);
    }
    public static int Fac(int n){
        if(n == 1){//初始条件
            return 1;
        }
        return n*Fac(n-1);
    }

“递”与“归”的过程分析：

示例二：没有返回值方法的递归—>按顺序打印1949

//递归打印实现：按顺序分别打印出1949的每位数字：1 9 4 9
    public static void main(String[] args) {
        int year = 1949;
        print(year);
    }
    public static void print(int n){
        if(n < 10){//初始条件 
            System.out.print(n+" ");
        }else{
            print(n/10);
            System.out.print(n%10+" ");
        }
    }

“递”与“归”的过程分析：

注意：如果代码写成这样程序会陷入死循环：

public class TestDemo {
    //递归打印实现：按顺序分别打印出1949的每位数字：1 9 4 9
    public static void main(String[] args) {
        int year = 1949;
        print(year);
    }
    public static void print(int n){
        if(n < 10){//初始条件
            System.out.print(n+" ");
        }
            print(n/10);
            System.out.print(n%10+" ");
    }

这是因为当n=1时，打印完了1之后，代码继续往下执行，又会执行print(n/10),此时n=0,因此又会打印0，然后又执行print(n/10),0/10==0,所以又会打印0，然后依次循环这个步骤，因此会陷入死循环。

好了，这篇文章先讲解到这里，下一篇文章会讲一些递归的练习题以及递归当中追经典的青蛙跳台阶和汉诺塔问题。

🌏🌏🌏今天的你看懂这里又学到了很多东西吧🌏🌏🌏

🌔 🌔 🌔下次见喽🌔 🌔 🌔