数据结构与算法之树（六）

上节我们讲到了二叉树的前中后，层序遍历，下面我们来看实现：

定义一颗二叉树

  public class TreeNode {
      int val;
      TreeNode left;
      TreeNode right;
      TreeNode() {}
      TreeNode(int val) { this.val = val; }
      TreeNode(int val, TreeNode left, TreeNode right) {
      this.val = val;
      this.left = left;
      this.right = right;
      }
  }

前序遍历

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> preorderTraversal(TreeNode root) {
        helper(root);
        return list;
    }

    private void helper(TreeNode root) {
        if (root == null){
            return;
        }
        list.add(root.val);
        helper(root.left);
        helper(root.right);
    }
}

中序遍历

class Solution {
    List<Integer> list = new ArrayList<>();
    public List<Integer> inorderTraversal(TreeNode root) {
        helper(root);
        return list;
    }
    private void helper(TreeNode root){
        if(root == null){
            return;
        }
        helper(root.left);
        list.add(root.val);
        helper(root.right);
    }
}

后序遍历

class Solution {
   List<Integer> list = new ArrayList<>();
    public List<Integer> postorderTraversal(TreeNode root) {
        helper(root);
        return list;
    }

    private void helper(TreeNode root) {
        if (root == null){
            return;
        }
        helper(root.left);
        helper(root.right);
        list.add(root.val);
    }
}

层序遍历 

class Solution {
    List<List<Integer>> lists = new ArrayList<>();
    public List<List<Integer>> levelOrder(TreeNode root) {
        dfs(root,0);
        return lists;
    }

    private void dfs(TreeNode root, int height) {
        if (root == null){
            return;
        }
        if (lists.size() == height){
            lists.add(new ArrayList<>());
        }
        List<Integer> list = lists.get(height);
        list.add(root.val);
        dfs(root.left,++height);
        dfs(root.right,height);
    }
}

class Solution {
 public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> lists = new ArrayList<>();
        if (root == null){
            return lists;
        }
        Queue<TreeNode> queue = new ArrayDeque<>();
        queue.offer(root);
        while (!queue.isEmpty()){
            int count = queue.size();
            List<Integer> list = new ArrayList<>();
            for (int i = 0; i < count; i++) {
                TreeNode treeNode = queue.poll();
                if (treeNode.left != null){
                    queue.offer(treeNode.left);
                }
                if (treeNode.right != null){
                    queue.offer(treeNode.right);
                }
                list.add(treeNode.val);
            }
            lists.add(list);
        }
        return lists;
    }
}

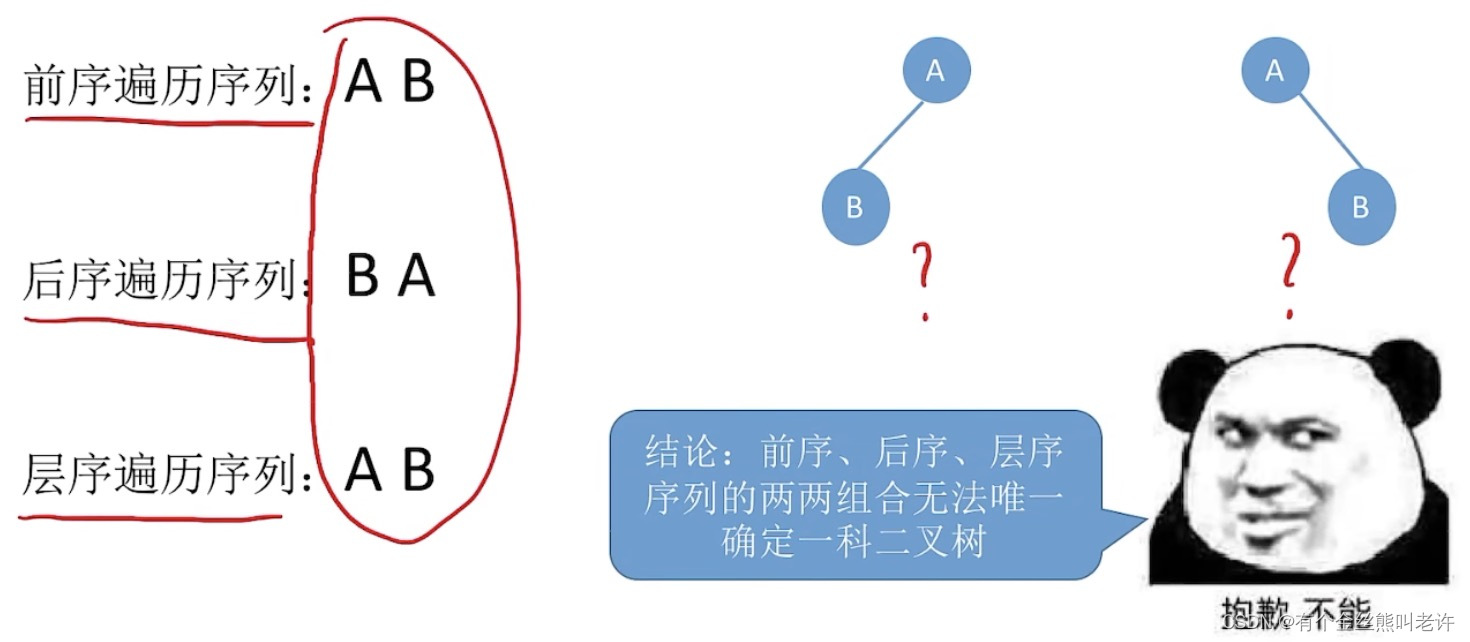
二叉树遍历序列构造二叉树

 

 如果脱离中序遍历，是不能构造出唯一一颗二叉树的

线索二叉树

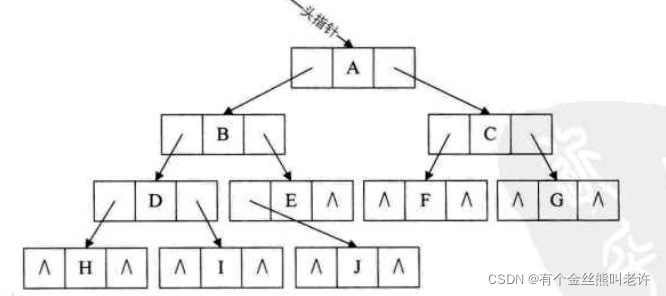
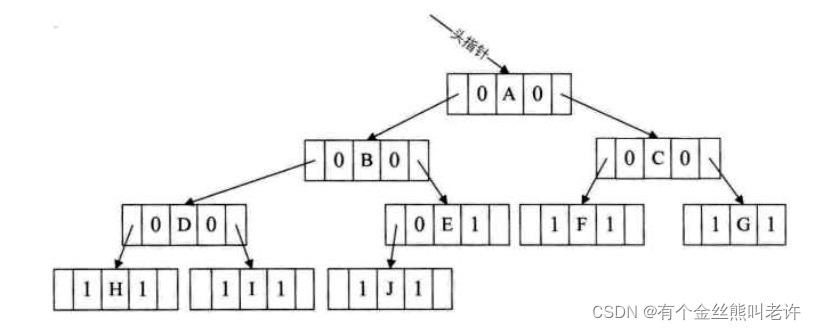
我们来观察上图，发现指针域并不是都充分的利用了，有许许多多的“^”，也就是空指针域的存在，这实在不是好现象，我们要利用起来。

我们可以考虑利用那些空地址，存放指向结点在某种遍历次序下的前驱和后继结点的地址。就好像GPS导航仪一样，我们开车的时候，哪怕我们对具体目的地的位置一无所知，但它每次都可以告诉我从当前位置的下一步应该走向哪里。这就是我们现在要研究的问题。我们把这种指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树就称为线索二叉树(Threaded BinaryTree)。

我们把下图的二叉树进行中序遍历后，将所有的空指针域中的 right ，改为指向它的后继结点。于是我们就可以通过指针知道H的后继是D(图中1)，I的后继是B(图中②)J的后继是E(图中③)，E的后继是A(图中④)，F的后继是C(图中⑤)，G的后继因为不存在而指向NULL(图中⑥)。此时共有6个空指针域被利用。

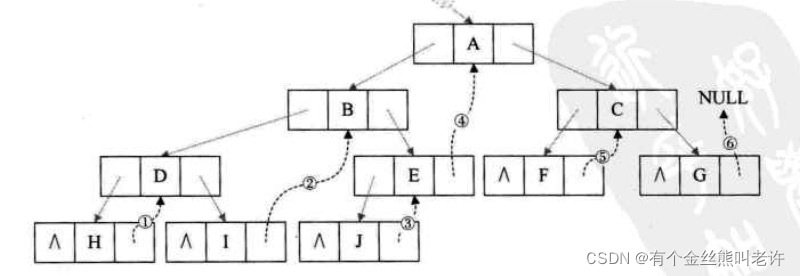
我们将这棵二叉树的所有空指针域中的 left ，改为指向当前结点的前驱。因此H的前驱是NULL(图中①)I的前驱是D(图中②)，J的前驱是B(图中③)，F的前驱是A(图中④)G的前驱是C(图中⑤)。一共5个空指针域被利用，正好和上面的后继加起来是11个。

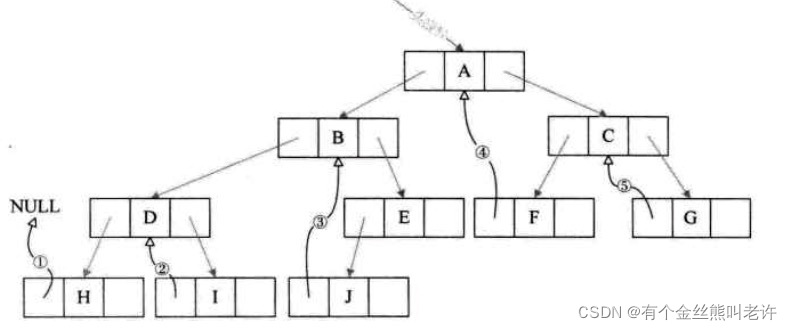
其实线索二叉树，等于是把一棵二叉树转变成了一个双向链表，这样对我们的插入删除结点，查找某个结点都带来了方便，我们对二叉树以某种次序遍历使其变为线索二叉树的过程称作是线索化。

不过好事总是多磨的，问题并没有彻底解决。我们如何知道某一结点的left是指向它的左孩子还是指向前驱?right是指向右孩子还是指向后继?比如E结点的left是指向它的左孩子而right却是指向它的后继A。显然我们在决定left是指向
左孩子还是前驱，right是指向右孩子还是后继上是需要一个区分标志的。因此，我们在每个结点再增设两个标志域ltag和rtag，注意ltag和rtag只是存放0或1数字的变量，其占用的内存空间要小于像left和right的指针变量。结点结构如下：

ltag为0时指向该结点的左孩子，为1时指向该结点的前驱。
rtag为0时指向该结点的右孩子，为1时指向该结点的后继。

 代码实现如下：

class TreeNode<T> {
    T data;
    TreeNode<T> left;
    TreeNode<T> right;
    int leftType;  // 0 代表left是左子树 1代表left是前驱结点
    int rightType; // 0 代表right是左子树 1代表right是后继结点
}

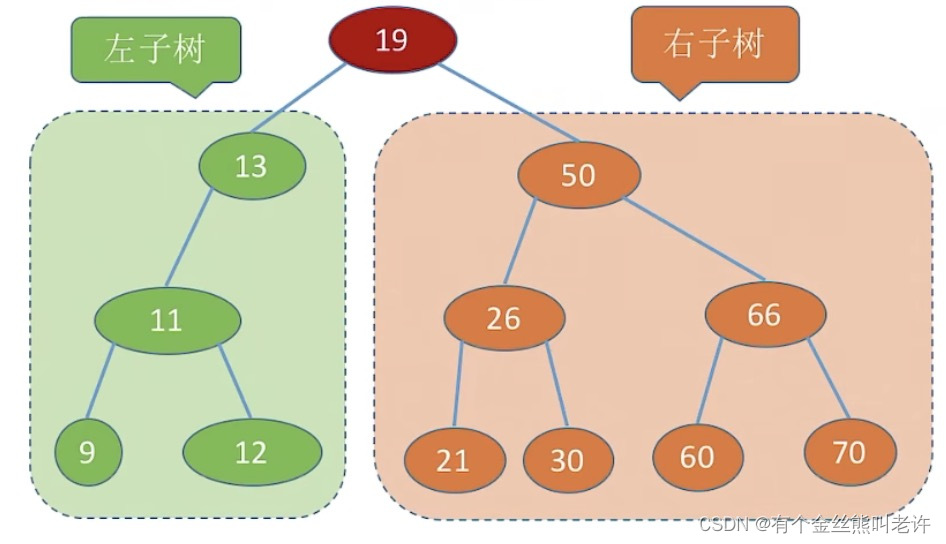
二叉排序树

又称二叉查找树，具有如下性质：

左子树上所有结点的关键字均小于根结点的关键字;

右子树上所有结点的关键字均大于根结点的关键字。

左子树和右子树又各是一棵二叉排序树。

进行中序遍历，可以得到一个递增的有序序列 。

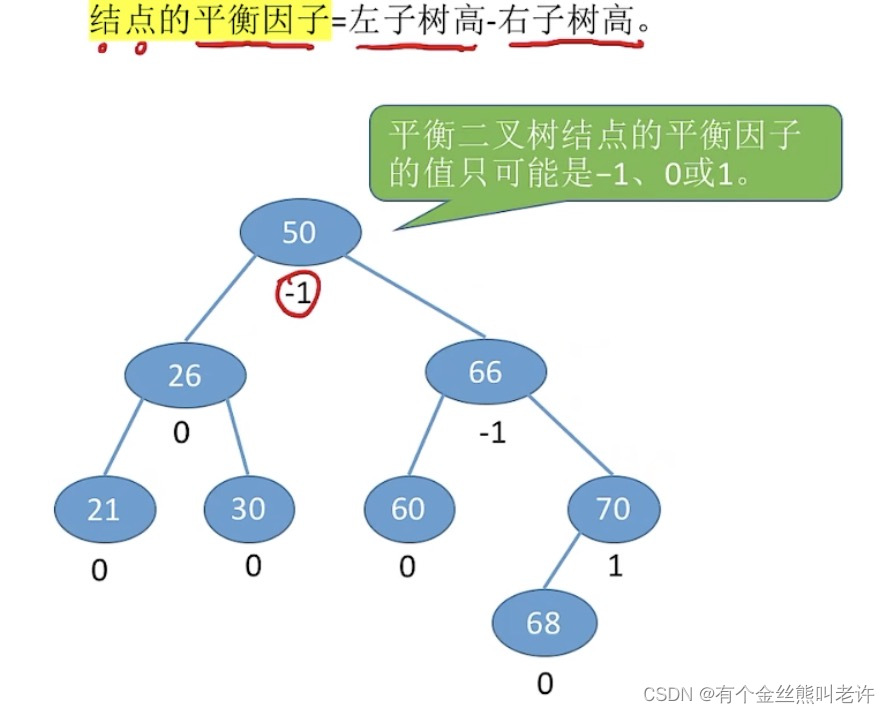
平衡二叉树

平衡二叉树(Balanced Binary Tree)，简称平衡树(AVL树) 一树上任一结点的左子树和右子树的 
高度之差不超过1。