一本通-1314：【例3.6】过河卒

【题目描述】

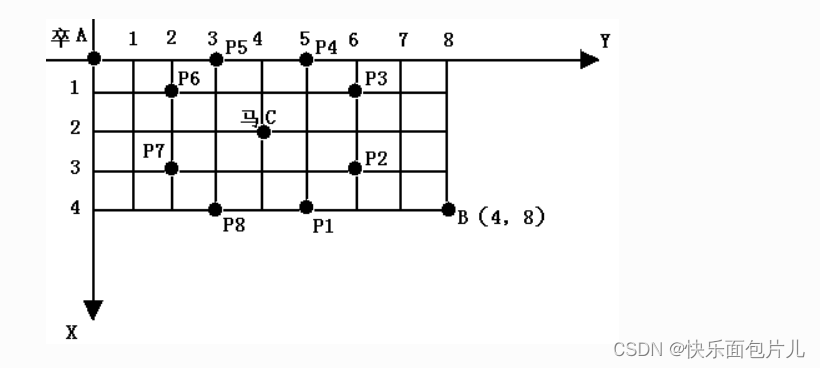
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

【输入】

给出n、m和C点的坐标。

【输出】

从A点能够到达B点的路径的条数。

【输入样例】

8 6 0 4

【输出样例】

1617

思路：

典型运用递推算法进行求解的问题，在这道题中我们要确定好边界还有递推关系式，唯一的难点就是这道题中对马的标记还要判断马越不越界的情况，由于最后结果可能非常大我们这里还是用long long 类型，我们可以看到想要知道到B有多少种方法就要知道他前面有多少种，一直往前推所以要从最开始推理，到每个点的条数（除掉下x,y轴边界都是1条路经）其余都等于左边条数+上边条数，由此我们就可以确定边界和递推关系式，最后就是要找好马的控制点（排除越界的情况）即可。

#include<iostream>
using namespace std;
#define int long long
//边界
//i==1 || j=1  f[i][j]=1,马的控制点要单独处理
//递推关系式
//f[i][j]=f[i-1][j]+f[i][j-1]

const int N = 1e2 + 10;
int f[N][N];//递推数组
//f[i][j] 从起点0,0到i，j点路径的数量
bool vis[N][N];//二维标记数组，标记马的控制点
int n, m, cx, cy;
//方向数组
//          p2 p7 p3 p6 p1 p8 p4 p5
int dx[] = { 1,1,-1,-1, 2, 2, -2,-2 };
int dy[] = { 2,-2,2,-2, 1, -1, 1,-1 };
signed main() {
	cin >> n >> m >> cx >> cy;
	vis[cx][cy] = 1;//马这个点标记
	//标记所有马的控制点
	for (int i = 0; i < 8; i++) {
		int bx = cx + dx[i], by = cy + dy[i];
		//如果新生成的坐标越界了，则continue跳过，继续生成下一个坐标
		if (bx<0 || bx>n || by<0 || by>m) continue;
		vis[bx][by] = 1;
	}
	//1.边界
	f[0][0] = 1;
	//处理了第一行
	for (int j = 1; j <= m; j++) {
		f[0][j] = f[0][j - 1];
		if (vis[0][j]) f[0][j] = 0;
	}
	//处理了第一列
	for (int i = 1; i <= n; i++) {
		f[i][0] = f[i - 1][0];
		if (vis[i][0]) f[i][0] = 0;
	}

	//2.递推
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			f[i][j] = f[i - 1][j] + f[i][j - 1];
			if (vis[i][j]) f[i][j] = 0;
		}
	}

	cout << f[n][m] << endl;
	return 0;
}