Java 172.阶乘后的零

最新推荐文章于 2026-01-05 17:06:32 发布

原创最新推荐文章于 2026-01-05 17:06:32 发布 · 606 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#java #leetcode

Java 专栏收录该内容

7 篇文章

订阅专栏

该博客介绍了一个LeetCode题目，要求计算给定整数n的阶乘n!中尾随零的数量。解题关键在于理解阶乘中尾随零是由2和5的乘积决定的，而5的因子比2的因子少，因此主要关注5的因子数量。通过分析发现，只需要计算n!中包含多少个5即可。示例中，3!没有尾随零，5!有一个尾随零，0!也有0个尾随零。

题目描述：

给定一个整数 n ，返回 n! 结果中尾随零的数量。

提示 n! = n * (n - 1) * (n - 2) * ... * 3 * 2 * 1

输入示例：

示例 1：

输入：n = 3
输出：0
解释：3! = 6 ，不含尾随 0

示例 2：

输入：n = 5
输出：1
解释：5! = 120 ，有一个尾随 0

示例 3：

输入：n = 0
输出：0

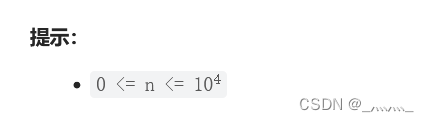
代码结构：

class Solution {
    public int trailingZeroes(int n) {
        
    }
}

解题思路：

因为是乘法，所以有多少个2*5末尾就有多少个0

这道题可以转换成寻找阶乘中有多少个2*5，因为每两个数就可以分解为2*x，每五个数可以分解为5*x，5的个数少于2的个数，所以只需要找到有多少个5就可以解决问题。

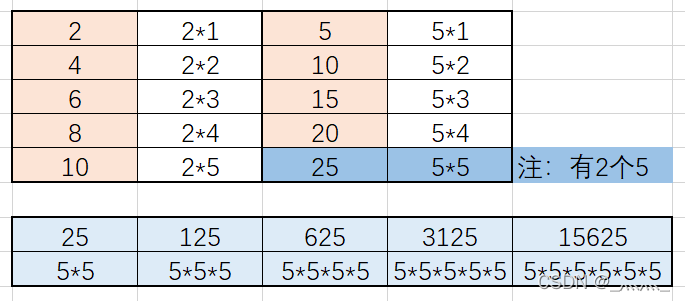
由题目和上图知，最多直到3125，即包含五个5

假如计算30！，从1到30，其中5、10、15、20、25和30都是5的倍数。25是5的平方，所以有7个零。

public int trailingZeroes(int n) {
        int count = 0;
        int count1 = 0;
        int count2 = 0;
        int count3 = 0;
        int count4 = 0;
        int count5 = 0;
        count1 = n / 5;
        count2 = count1 / 5;
        count3 = count2 / 5;
        count4 = count3 / 5;
        count5 = count4 / 5;
        count = count1 + count2 + count3 + count4 + count5;
        return count;
    }

代码再经过简化后，即

public int trailingZeroes(int n) {
        int count = 0;
        while (n >= 5){
            count += n / 5;//count = count + n / 5;
            n = n / 5;
        }
        return count;
    }