数据与结构

数据结构：描述从现实中抽象出数据模型，即数据关系的抽象

逻辑结构：数据之间的逻辑关系

表，队列，栈：线性结构，数据之间是线性关系，一一对应

树：非线性结构，一对多

图：非线性结构，多对多

存储结构：对数据以及数据关系的存储

连续存储：将所有数据放到一起

离散存储：数据可能分布在内存的不同位置

对数的操作（算法）：

不是简单的数值操作而是一些逻辑操作

增：增加数据

删：删除数据

改：修改数据

查：查找或遍历数据

算法：就是对某个动作的操作流程或步骤

算法特性：

1.可行性：可以实现，每个计算步骤能够在有限的时间内完成

2.确定性：没有歧义，步骤唯一且确定

3.有穷性：有明确的目标且可到达，步骤是有限的

4.有一个或多个输入

5.有一个或多个输出

算法优劣评判标准：

时间复杂度：语句执行的频度，与算法程序执行的时间没有必然关系

执行的频度：算法中语句执行的次数与输入问题规模的比值

度量一个算法的时间复杂度通常使用其量级表示

空间复杂度：占用内存的多少

常见数据结构：

1.表结构  线性结构

数据逻辑组织为表形式，逻辑上，数据是连续排列的

每个节点（除头尾外），都有且仅有一个前驱和一个后继

头节点：只有后继没有前驱

尾节点：只有前驱没有后继

节点：数据逻辑的最小单元

存储结构：

顺序存储：数组存储

顺序表：存储上连续存储，逻辑上是表结构

离散存储：链式存储

链表：存储上使用离散存储，逻辑上是表结构

顺序表：

表结构定义：

1.定义节点类型，假设为int

typedef int  Data_t;
2.定义顺序表结构

动态长度：

typedef struct list_t
{
    int max_len; //存储顺序表的最大长度
    int cnt;     //存储当前表中节点个数
    Data_t *data;//存储节点的数组动态分配长度
};
固定长度：

define  MAXLEN  20
typedef struct list_t
{
    int cnt;     //存储当前表中节点个数
    Data_t data[MAXLEN]; //静态分配数组长度
};
顺序表的操作：

1.创建表：动态长度表为例

2.销毁表：

3.增加节点，插入数据

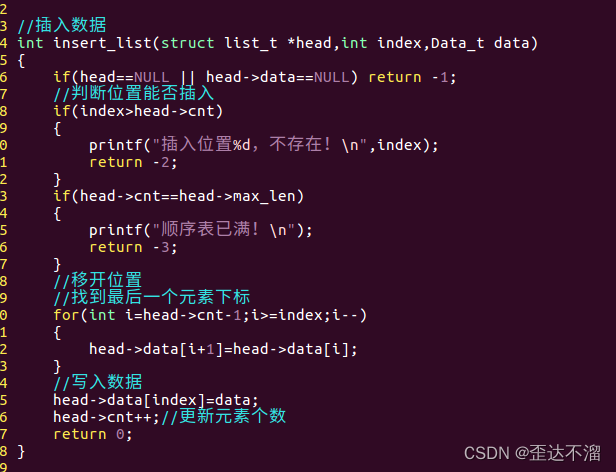
 4.遍历，获取某个节点数据

 

表的离散存储：链表

逻辑结构：表结构，通过指针方式实现逻辑上的链接。

1.定义数据类型

2.定义节点类型

 

链表中的一些情况的表示：

链表结尾节点表示：指针域==NULL

空链表表示：使用一个不存储数据的节点作为头节点。当头节点的指针域==NULL表示空链表

创建空链表：

 

插入数据：

给定一个下标，删除该节点：

 给定节点的地址删除该节点：

 

修改下标位置的值：

链表拼接：

链表的翻转：

链表域顺序表的优劣：

链表根据节点长度动态分配，没有长度限制。

链表的插入和删除节点，时间复杂度比顺序表优秀，不会存在大片数据整体移动的情况。

顺序表存储密度高，不会有指针域浪费空间，顺序表的随机访问效率高。

静态链表：链表的节点事先已经开辟了（节点数组），动态下标或指针域来了建立逻辑关系

队列：是一种特殊的线性表，规定了表的入口和出口，同时先进先出，多用于缓冲。

队列的实现：

顺序存储的队列：循环队列

离散存储的队列：链式队列

循环队列：

1.创建空队列

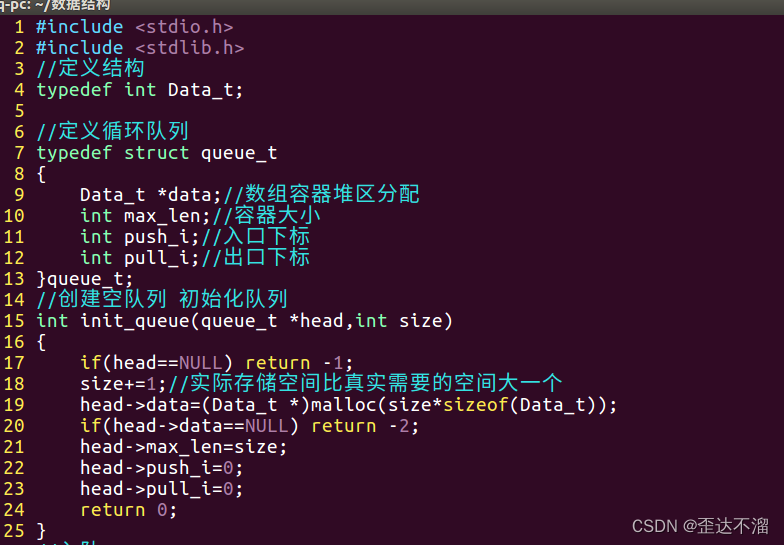
2.销毁队列

 

3.入队

4.出队

5.置空队列

6.获得队列长度

链表的思考题：

已知一个单向链表的某个节点地址p,如何判断这个链表中是否有环？

答：使用一个辅助表，将遍历过的节点地址放入该表，每次移动节点指针p时，对该表进行比较，若p出现在该表中则存在环。

已知一个单向链表的某个节点地址p，p不是最后一个节点，问在不知道头节点地址的情况下能否删除该节点？

答：将后一个节点数据移动到p节点数据域p->data=p->next->data;备份q q=p->next;修改指向：p->next=q->next;释放p的后一个节点：free(q);

栈：一种特殊的线性表：只能在表的一端进行插入和删除，后进先出

顺序栈：数组，从数组尾部进行插入和删除

四种类型的栈：

增栈：入栈时，栈顶指针向大地址方向移动

减栈：入栈时，栈顶指针向小地址方向移动

空栈：栈顶指针指向的位置数据无效

满栈：栈顶指针指向的位置数据有效

链式栈：链表，从头部插入和删除

树：一个节点有0个或多个直接后继节点，有1个（子节点）或0个（根节点）直接前驱。（不能有环结构）

根节点：树的起始位置，一棵树一定有根节点

子节点：树结构中除根节点外其他节点都称作子节点

树的度：以树中直接后继最多的节点个数称该树的度

树的深度：从根开始到每一个叶子节点最长的经过的节点个数，即树的层数

树的路径：从根节点开始到目标节点经过的节点顺序

子树：一棵树中的一部分节点构成的一棵树称该树是其子树

数据结构中主要研究二叉树

二叉树：一个度为2的树

1.二叉树有0个或1个或2个直接后继节点，且严格区分左右，即使只有一个子节点也要区分左右。

2.一个二叉树其子树也一定是二叉树。

二叉树（Binary Tree ）是n（n≥0）个节点的有限集合，它或者是空集（n＝0），或者是由一个根节点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成。
二叉树与普通有序树不同，二叉树严格区分左孩子和右孩子，即使只有一个子节点也要区分左右。

二叉树的特例：

满二叉树：除叶子节点外，其他所有节点都有两个直接后继，且叶子节点都在最后一层。

完全二叉树：只有最下面两层有度数小于2的节点，且最下面一层的叶节点集中在最左边的若干位置上。除最底层没有排满外，其它层均排满且每一层都需要按照先左后右的顺序排列。

带权二叉树：二叉树的路径上带有权值

二叉树的一些特性：

1.在二叉树的第i层上至多有2的i-1次方个结点  2^(n-1)
2.深度为k的二叉树至多有2的k次方-1个结点    2^k -1
3.对任何一棵二叉树T，如果其终端结点数为n0，度为2的结点n2，那么n0=n2+1，叶子节点的个数始终比度为2的节点个数多 1个
4.具有n个结点的完全二叉树的深度为 = (log2n)+1 取整数 
        第n号节点  是  (log2n)+1  取整  行
        
5.对一棵有n个结点的完全二叉树的结点按层序编号（从第一层到最后一层，每层从左至右），对任一结点i（1<i<n）有：
     a.如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是结点i/2 取整;
     b.如果2i>n，则结点i无左孩子（即为叶子结点）；否则其左孩子结点是2i；（偶数个结点，最后一个叶子结点一定是左）
     c.如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1；（奇数个结点，最后一个叶子结点一定是右）

 

二叉树的遍历：

1.层次遍历：从上到下，从左到右依次遍历

2.深度遍历：

先序遍历：先遍历根节点，再遍历左节点，最后 遍历右节点

中序遍历：先遍历左节点，再遍历根节点，最后遍历右节点

后序遍历：先遍历左节点，再遍历右节点，最后遍历根节点

先序或后续遍历可以确定根节点，先序第一个就是根节点，后序最后一个是根节点，中序可以确定左右子树。

图：网结构

是一种比表更复杂的数据结构，树是特殊的图。

图有多个直接前驱，有多个直接后继。

专业术语：

顶点：图（网）中存储数据的节点

边/弧：顶点与顶点间的关系，没有方向称边，有方向称弧

边/弧的权值：从一个顶点到另一个顶点的代价

子图：图中的一部分节点以及这些节点的边构成子图

路径：从一个顶点到另一个顶点所经过的边

简单路径：路径中所经过的顶点没有重复的

有向图： 边有方向
无向图： 边没有方向
有环图：有路径构成环
无环图：没有路径可以构成环    
带权图: 边有权值 
无权图: 边没有权值 
连通图: 任意两个顶点都有路径可以到达 

一个连通图有n个节点，有n(n-1)/2条边，有n(n-1)条弧

图的存储：

顺序存储：节点：数组      边：领接矩阵，适应于稠密图或节点较少的图，消耗内存较多

完全图：边=n(n-1)或n(n-1)/2，有所有的边