【数据结构】图的应用---最小生成树(Prim,Kruskal)、最短路径(BFS,Dijkstra,Floyd)、拓扑排序、关键路径、有向无环图表达式

本文链接：https://blog.youkuaiyun.com/m0_61628700/article/details/138747797

文章目录

- 5.图的应用

5.图的应用

5.1 最小生成树

定义

对一个带权连通无向图 $G = (V, E)$ ，生成树不同，每棵树的权（即树中所有边上的权值之和）也可能不同。

设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树（MST）。
性质

1.最小生成树可能有多个，但边的权值之和总是唯一且最小的；

2.最小生成树的边数=顶点数-1。砍掉一条则不连通，增加一条会出现回路；

3.如果一个连通图本身就是一棵树，则其最小生成树就是它本身；

4.只有连通图才有最小生成树，非连通图只有生成森林。
注

最小生成树是所有边权值之和最小，但不能保证任意两个顶点之间的路径最短。如：

伪代码

GENERIC_MST(G){
     
    T=NULL;
    while T未形成一棵生成树;
    	do 找到一条最小代价边(u,v)并且加入T后不会产生回路;
    		T=T∪(u,v);
}

通用算法每次加入一条边以逐渐形成一棵生成树。

5.1.1 Prim算法

定义

从某一个顶点开始构建生成树；

每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。
- 即选最小权值的结点
时间复杂度

$O(|V|^2)$ ，适用于稠密图（|E|大的）。
算法的实现思想
- 思路：
  
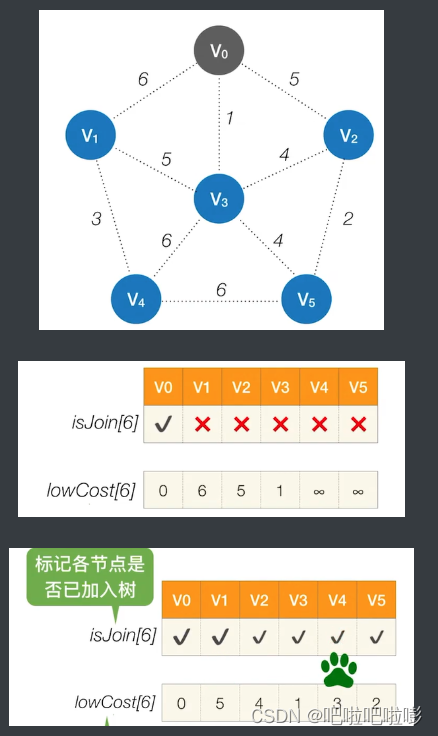
  1.从 $V_0$ 开始，总共需要n-1轮处理。
  
  2.第一轮处理：循环遍历所有个结点，找到lowCast最低的，且还没加入树的顶点。
  
  3.再次循环遍历，更新还没加入的各个顶点的lowCast值。
  
  每一轮时间复杂度 $O (2 n)$ ，一共有n轮。
- 代码步骤：
  
  1.创建isJoin数组，初始为false，判断结点是否加入树。
  
  2.创建lowCost数组，用于存储到该结点的最短距离。
  
  3.从 $v_0$ 开始，将与其连接的权值加入到lowCost数组中。
  
  4.遍历lowCast数组，找到最小值，将其加入树中，并继续遍历与其相连的边。

伪代码

void Prim(G,T){
     
    T=∅; //初始化空树
    U={
     w}; //添加任意一个顶点w
    while((V-U)!=∅){
      //若树中不含全部顶点
        设(u,v)是使u∈U与v∈(V-U),且权值最小的边;
        T=T⋃{
     (u,v)}; //边归入树
        U=U⋃{
     v}; //顶点归入树
    }
}

5.1.2 Kruskal算法

定义

每次选则一条权值最小的边，使这条边的两头连通（原本已经连通的不选），直到所有结点都连通。
- 即每次选最小的边
时间复杂度

$O(|E|log_2|E|)$ ，适用于边稀疏图。
算法的实现思想
- 思路：
  
  1.初始：将各条边按权值排序。
  
  2.共执行e轮，每轮判断两个顶点是否属于同一集合，需要 $O(log_2e)$

伪代码

void Kruskal(V,T){
     
    T=V; //初始化树T，仅含顶点
    numS=n; //连通分量数
    while(numS>1){
      //若连通分量数大于1
        从E中取出权值最小的边(v,u);
        if(v和u属于T中不同的连通分量){
      //就是没有形成环
            T=T⋃{
     (v,u)}; //将此边加入生成树中
            numS--; //连通分量数减1
        }
    }
}

5.1.3 最小生成树代码

A.邻接矩阵

#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <limits.h>

#define V 5 // 图的顶点数

// 找到距离集合最近的顶点
int min_key(int key[], bool mst_set[]) {
   
    int min = INT_MAX, min_index;
    for (int v = 0; v < V; v++) {
   
        if (mst_set[v] == false && key[v] < min) {
   
            min = key[v];
            min_index = v;
        }
    }
    return min_index;
}

// 打印最小生成树
void print_mst(int parent[], int graph[V][V]) {
   
    printf("Edge   Weight\n");
    for (int i = 1; i < V; i++)
        printf("%d - %d    %d \n", parent[i], i, graph[i][parent[i]]);
}

// Prim算法
void prim_mst(int graph[V][V]) {
   
    int parent[V]; // 存放最小生成树的父节点
    int lowCost[V];    // 用于存放顶点到最小生成树的最小权重
    bool isJoin[V]; // 记录顶点是否已经加入最小生成树

    for (int i = 0; i < V; i++) {
   
        lowCost[i] = INT_MAX;
        isJoin[i] = false;
    }

    lowCost[0] = 0; // 初始点为0
    parent[0] = -1; // 根节点没有父节点

    for (int count = 0; count < V - 1; count++) {
   
        int u = min_key(lowCost, isJoin);
        isJoin[u] = true;

        for (int v = 0; v < V; v++) {
   
            if (graph[u][v] && !isJoin[v] && graph[u][v] < lowCost[v]) {
   
                parent[v] = u;
                lowCost[v] = graph[u][v];
            }
        }
    }

    print_mst(parent, graph);
}

// Kruskal算法

// 结构体用于表示边
struct Edge {
   
    int src, dest, weight;
};

// 比较函数，用于排序
int compare(const void* a, const void* b)