【Leetcode】11. 盛最多水的容器

目录

记得点个赞哦 

代码详解

复杂度分析：

双指针法

什么是双指针法？

双指针法的应用

总结

---

---

记得点个赞哦 

简介： 这个题解将解决LeetCode 11题，要求找到可以容纳最多水的容器。我们将采用双指针法来优化解决这个问题的方法。

问题描述：

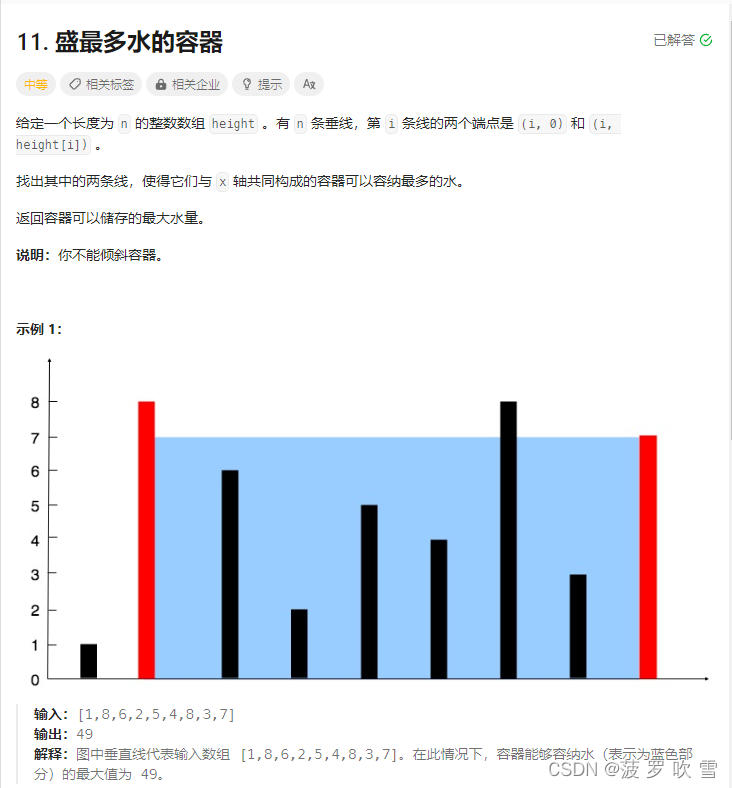
给定一个整数数组 height，数组中的每个元素代表一根垂直线的高度。我们需要找到两根垂直线，它们与x轴一起构成一个容器，可以容纳最多的水。

解决方法：

传统的方法是通过嵌套循环来考虑所有可能的组合，但这种方法的时间复杂度为O(n^2)，效率较低。我们可以使用双指针法来优化解决这个问题的方法。

int findMinimum(int a, int b) {
    if (a < b) {
        return a;
    } else {
        return b;
    }
}
int maxArea(int* height, int heightSize) {
    int max = 0;
    int left = 0;
    int right = heightSize - 1;

    while (left < right) {
        int h = findMinimum(height[left], height[right]);
        int w = right - left;
        int area = h * w;
        max = (area > max) ? area : max;

        if (height[left] < height[right]) {
            left++;
        } else {
            right--;
        }
    }

    return max;
}

在上面的代码中，我们维护了两个指针 left 和 right，并使用 findMinimum 函数来找到两个指针所指的垂直线的最小高度。然后，我们计算容器的面积，即两个指针之间的距离乘以较小高度的那个垂直线。

代码详解

这段代码的作用是找到可以容纳最多水的容器，也就是找到两根垂直线，它们与 x 轴一起构成的容器可以容纳最多的水。现在，让我逐行解释代码：

1. int maxArea(int* height, int heightSize) {: 这是函数的定义，接受一个整数数组 height 和数组的大小 heightSize 作为输入参数，返回一个整数，表示最大的容器面积。

2. int max = 0;: 创建一个整数变量 max 并初始化为 0，用来存储最大的容器面积。

3. for (int i = 0; i < heightSize; i++) {: 这是一个外层循环，用于遍历数组中的每一个垂直线，其中 i 是当前的左指针，从0到 heightSize-1。

4. for (int j = i + 1; j < heightSize; j++) {: 这是一个内层循环，用于遍历数组中从 i 后面一个位置开始的每一根垂直线，其中 j 是当前的右指针。

5. int h = findMinimum(height[i], height[j]);: 这一行计算当前容器的高度 h，通过调用 findMinimum 函数，该函数接受两个高度值，即 height[i] 和 height[j]，并返回较小的高度。

6. int w = j - i;: 这一行计算当前容器的宽度 w，即左指针和右指针之间的距离。

7. int area = h * w;: 这一行计算当前容器的面积 area，即高度乘以宽度。

8. max = (area > max) ? area : max;: 这一行比较当前容器的面积 area 是否大于已经存储的最大面积 max，如果是，就更新 max 为当前的 area，否则保持 max 不变。

9. 内层循环结束后，左指针 i 向右移动到下一个位置，继续遍历可能的容器。

10. 外层循环完成后，返回最大的容器面积 max，它代表了可以容纳最多水的容器的面积。

这段代码的核心思想是遍历所有可能的容器组合，计算它们的面积，并不断更新最大面积。然而，这种解决方法的时间复杂度是O(n^2)，因为它需要嵌套两个循环来考虑所有可能的组合，对于大规模的输入可能效率较低。你可以通过使用双指针法来优化解决这个问题的方法，如之前提供的双指针解决方法。双指针法的时间复杂度是O(n)，更高效。

复杂度分析：

这个优化的解决方法的时间复杂度是O(n)，其中n是数组的长度，因为我们只遍历数组一次。空间复杂度是O(1)，因为我们只使用了常数额外的空间。

双指针法

什么是双指针法？

双指针法，顾名思义，就是使用两个指针来解决问题。通常，这两个指针可以代表数组或字符串中的不同位置，然后根据问题的特定要求，移动这两个指针，执行比较、计算或其他操作。

在解决问题时，双指针法通常有以下几种常见的应用方式：

1. 对撞指针（Two Pointers）：这是最常见的双指针技巧，其中两个指针分别从数组或字符串的两端出发，然后逐渐向中间移动。这种方法通常用于查找两个数的和、判断回文串等。

2. 滑动窗口（Sliding Window）：滑动窗口是双指针法的一种变体，其中一个指针固定，而另一个指针可以在固定窗口大小内滑动。这种方法通常用于解决子数组或子字符串相关的问题，如找到包含特定元素的最短子数组。

3. 快慢指针（Fast and Slow Pointers）：这种方法通常用于查找链表中的环或中点等问题。一个指针移动速度快，另一个指针移动速度慢，它们一起遍历链表。

双指针法的应用

双指针法在解决各种算法问题中都有广泛的应用。以下是一些常见的问题，其中双指针法可以发挥作用：

1. 验证回文串

给定一个字符串，判断它是否是回文串。使用对撞指针，可以忽略非字母数字字符，然后从两端开始逐个字符比较，判断是否是回文串。

2. 找到两数之和

给定一个升序排列的数组和一个目标数，找到数组中两个数的和等于目标数。使用对撞指针，可以在数组两端开始查找，根据和与目标数的比较来移动指针。

3. 盛最多水的容器

给定一组垂直线段的高度，找到可以容纳最多水的容器。使用对撞指针，从两端开始向内移动指针，根据高度和距离计算容器的面积，并不断更新最大面积。

4. 判断链表是否有环

给定一个链表，判断是否存在环。使用快慢指针，一个指针每次移动一个节点，另一个指针每次移动两个节点，如果链表中存在环，这两个指针最终会相遇。

5. 找到无重复字符的最长子串

给定一个字符串，找到其中不含重复字符的最长子串的长度。使用滑动窗口，维护一个窗口，其中不包含重复字符的最长子串，通过移动窗口的左右边界来更新最大子串长度。

总结

双指针法是解决各种算法问题的强大工具，通过巧妙地移动指针来实现高效的算法。它适用于多种不同类型的问题，包括数组、字符串、链表和其他数据结构。通过深入理解双指针法的基本原理和不同应用方式，你可以更轻松地解决各种算法问题，并提高编程技能。希望这篇博客对你理解双指针法有所帮助，并能激发你解决算法问题的兴趣。