归并排序算法

一.算法思想理解

1.归并排序算法用的是分治思想，就是把复杂的问题分成简单的问题来解决。

2.解题思路：合并两个有序的数组大家应该都会吧（不难，后面也会讲哒），那么，我们如果将一个乱序数组从中间一直切分，一直切分到只有一个数时，这一个数组成的数组就可以看成是有序的，也就是到这一步我们的数组都是有序的了。然后我们再返回去，就是将这些有序的数组两两合并成新的有序数组，之后再合并，直到合并成了一个有序数组，就是我们的答案啦。

我们来举个例子：

（1）将无序数组按照一分为二一直划分成单个数字，此时，每一个数字我们可以看成是有序数组

    

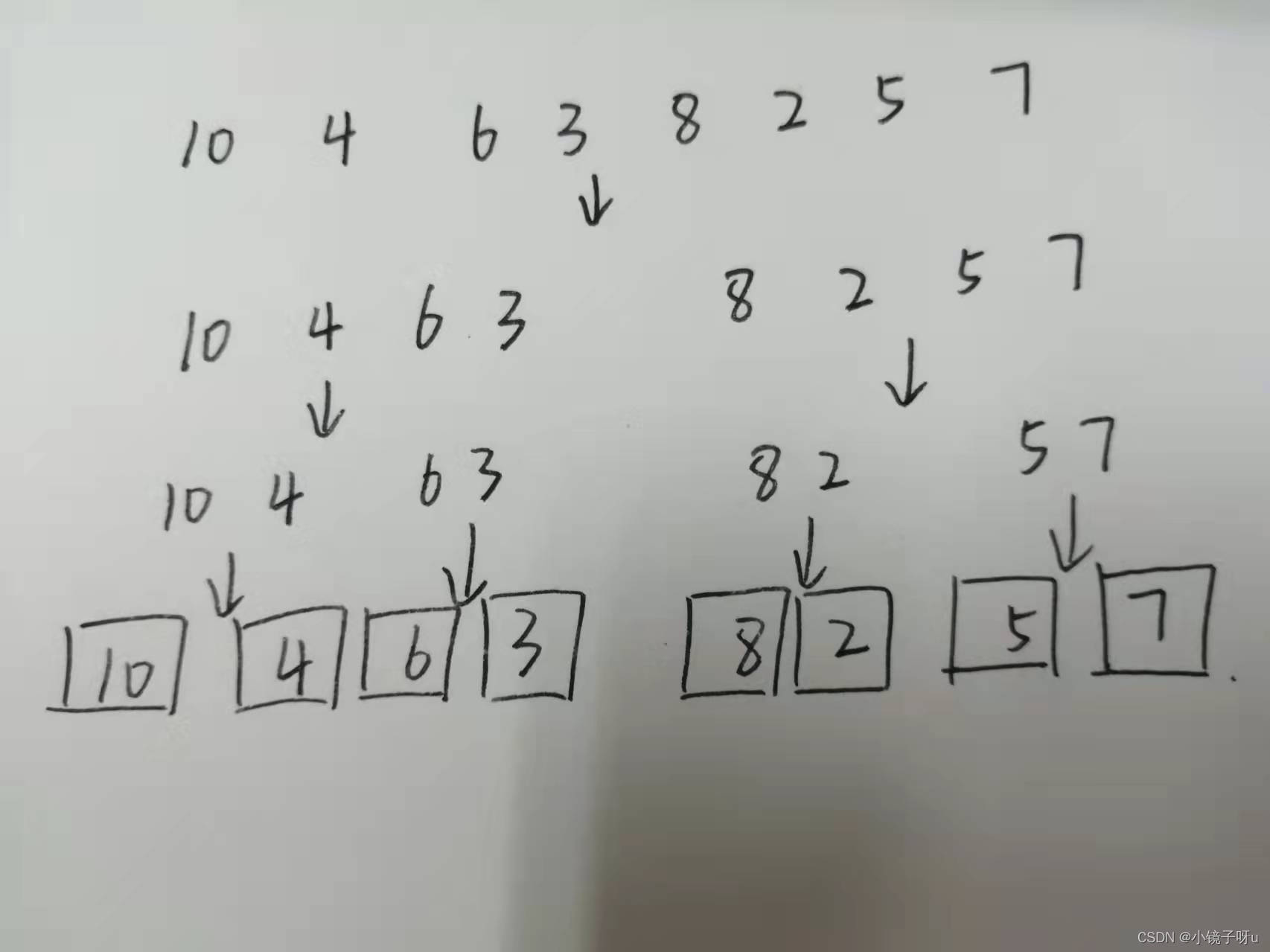
（2）合并有序数组：

我们合并两个有序数组，使之仍然有序的方法是：从两个数组的头一个元素开始，比较取出最小的数放入结果数组，再比较剩下部分的开头元素。

比如：

a1: 2 4 6 -->  2  4  6  -->  _  4  6  -->  _  4  6     -->  _  _  6         -->  _  _  6           -->  _  _  _

a2: 1 3 5 -->  _  3  5  -->  _  3  5  -->  _  _  5     -->  _  _  5         -->  _  _  _           -->  _  _  _

a:            --> 1           -->  1  2      -->  1  2  3     -->  1  2  3  4     -->  1  2  3  4  5   -->  1  2  3  4  5  6

那么，我们接下来再将刚刚分成的有序数组合并

就得到答案啦！

聪明的小伙伴可能发现了，解题的过程就是一层层的分，直到最小，再一层层的合，合成一个，这不就可以用递归来实现嘛！

二.代码实现

#include <iostream>
using namespace std;

#define MAX 10000
int tem[MAX];        // 用于暂时存储合并后的数组

/*
 *该函数用于合并两个有序数列[array_left,array_right),[array_right,end)
 *newArray[]      暂时存储合并后的数组
 *array[]         原始数组
 */
void merge(int newArray[],int array[],int array_left,int array_right,int end)
{
  int l = array_left,r = array_right,p = array_left;

//两个数组都没结束，l,r分别为两有序数列的开头
  while(l < array_right && r < end) 
  {
  	if(array[l] > array[r])
		  newArray[p++] = array[r++];
		else
		  newArray[p++] = array[l++];
	} 

//解决剩下没放进去的数
	while(l < array_right)         
	  newArray[p++] = array[l++];
	while(r < end)
	  newArray[p++] = array[r++];

//讲结果放到原始数组中
	for(int i = array_left; i < end; i++)
	{
		array[i] = newArray[i];
	}
} 


/*
 *归并函数
 *利用递归，分到只有一个元素为止，回退时将其合并
 */
void merge_sort(int l,int r,int a[])
{
	if(l >= r - 1) //只有一个元素 
	{
	  return;
	}

//分
	int mid = (r + l) / 2;
	merge_sort(l,mid,a);
	merge_sort(mid,r,a);

//合
	merge(tem,a,l,mid,r);
}


int main()
{
	int n, a[MAX];
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
	}
	merge_sort(0,n,a);
	for (int i = 0; i < n; i++)
	  cout << a[i] << " ";
	return 0;
}

over！