二维树状数组浅谈

今天本来刚学了初级的线段树，刷了几道水题之后在看那个势能线段树的入门知识，然后刚好旁边有道推荐二维树状数组的有趣的题目，所以来和大家分享一下~hh
                                                                                                 -----------蒟蒻成长日记7.26

洛谷P4514 上帝造题的七分钟
题目背景：略

输入格式

输入数据的第一行为 X n m，代表矩阵大小为  n×m。
从输入数据的第二行开始到文件尾的每一行会出现以下两种操作：

• L a b c d delta —— 代表将 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内的所有数字加上 deltadelta。
• k a b c d —— 代表求 (a,b),(c,d)(a,b),(c,d) 为顶点的矩形区域内所有数字的和。

请注意，k 为小写。

输出格式

针对每个 k 操作，在单独的一行输出答案。

输入输出样例

输入 #1复制

X 4 4
L 1 1 3 3 2
L 2 2 4 4 1
k 2 2 3 3

输出 #1复制

12

乍一看区间修改，区间查询 这道题好像是要跑线段树，本蒟蒻前天刚接触的线段树，只能写个简单的lazy，乍一想我也不会写多维的线段树~~~~咋办，看看题目标签吧，看到是树状数组和差分，然后就开始联系到上次提到的树状数组加推公式可以解决区间的修查问题，但是蒟蒻底子实在差，便跑去先补了个二维差分的知识点，确定了这个题要用差分才能切的时候，然后就来到了推公式环节~~~~就咋推都弄不明白（太菜了...）没办法苦苦煎熬了好久，本来就是想玩玩的，竟然把集训的题给旷了..，看题解思路的时候发现一个讲题的推荐了一篇博客，然后点进去，滑到推公式的那个环节，发现他讲的十分透彻，在这里也和大家分享一下。



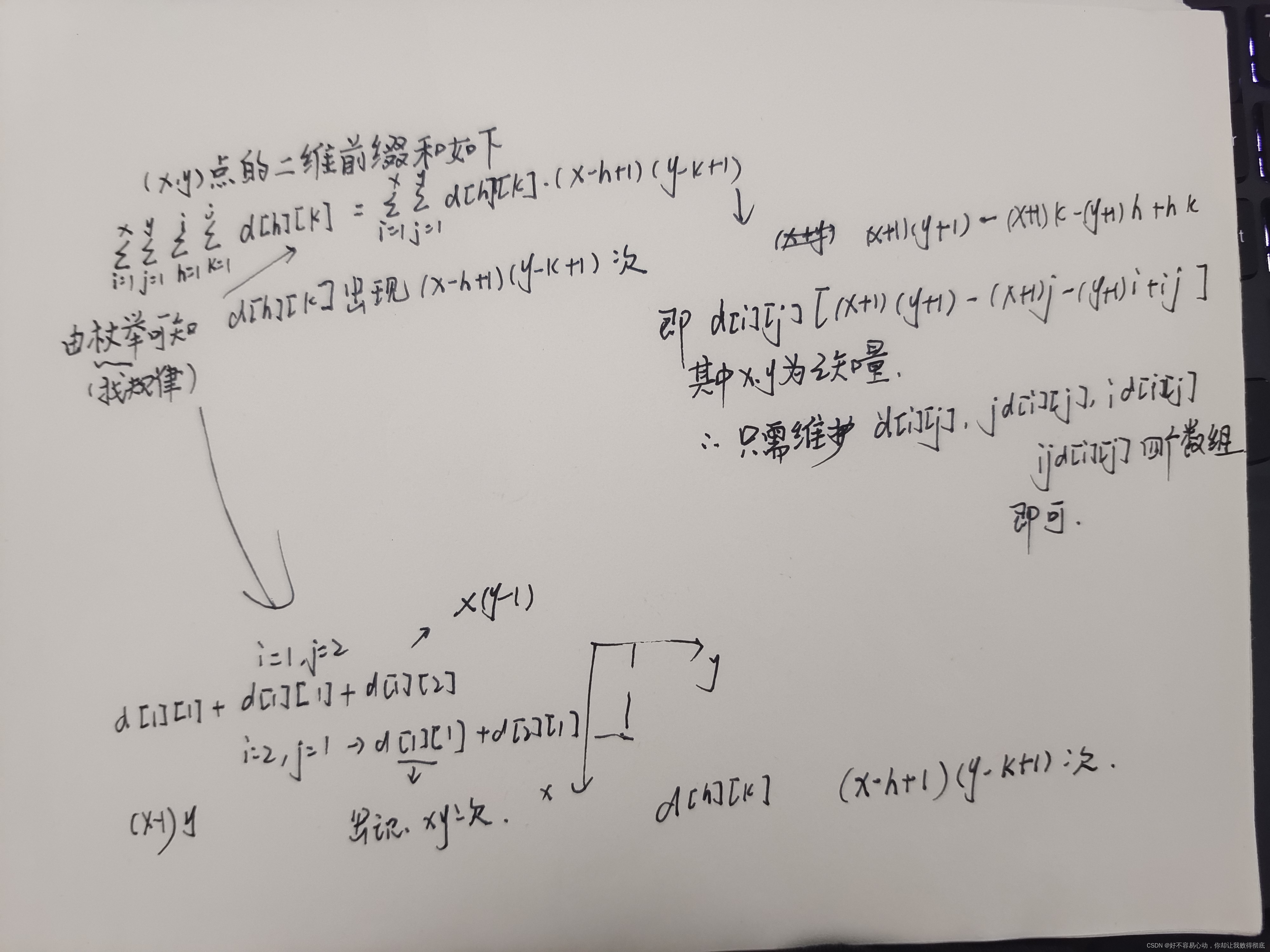
最后就是代码环节了，这个题是超有趣的，尤其是那个推公式环节。

#include<bits/stdc++.h>
using namespace std;
const int N=3e3+100;
int tr1[N][N],tr2[N][N],tr3[N][N],tr4[N][N];
typedef long long LL;
int n,m;
int lowbit(int x)
{
	return x&-x;
}
void add(int x,int y,LL c)
{
	if(x<1||x>n||y<1||m<y)return;
	for(int i=x;i<=n;i+=lowbit(i))
	 for(int j=y;j<=m;j+=lowbit(j))
	  {
	  	tr1[i][j]+=c;
	  	tr2[i][j]+=c*y;
	  	tr3[i][j]+=x*c;
	  	tr4[i][j]+=c*x*y;
	  }
	  
}
void add_range(int x1,int y1,int x2,int y2,LL c)
{
	add(x1,y1,c);
	add(x2+1,y1,-c);
	add(x1,y2+1,-c);
	add(x2+1,y2+1,c);
}
int sum(int x,int y)
{
	int res=0;
	for(int i=x;i;i-=lowbit(i))
	 for(int j=y;j;j-=lowbit(j))
	   res+=tr1[i][j]*(x+1)*(y+1)-tr2[i][j]*(x+1)-tr3[i][j]*(y+1)+tr4[i][j];
	   
	return res;
}
int sum_range(int x1,int y1,int x2,int y2)
{
	return sum(x2,y2)-sum(x2,y1-1)-sum(x1-1,y2)+sum(x1-1,y1-1);
}
int main()
{
	char op[2];
	int x1,y1,x2,y2,d;
	cin>>op>>n>>m;
	while(~scanf("%s",op))
	{
		if(*op=='L')
		 {
		 	scanf("%d%d%d%d%d",&x1,&y1,&x2,&y2,&d);
		 	add_range(x1,y1,x2,y2,d);
		 }
		 else 
		 {
		 	scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		 	printf("%d\n",sum_range(x1,y1,x2,y2));
		 }
		
	}
 } 

参考资料：高级树状数组——区间修改区间查询、二维树状数组 - 胡小兔 - 博客园 (cnblogs.com)