第一周：李宏毅机器学习

目录

摘要

Abstract

一、机器学习的基本概念

机器学习的任务

二、机器找模型的方法

1、定义一个带有未知参数的函数

2、定义损失函数 

 3、最佳化

三、更复杂的模型

1、分段线性函数(Piecewise Linear Function)的表示 

2、连续曲线的表示 

3、Hard Sigmoid的Sigmoid表示

4、更新初始定义的模型 

5、定义新模型的损失函数

6、新模型的最佳化

7、Hard Sigmoid的ReLU表示

8、神经网络 

 四、深度学习

 1、前反馈全连接网络（Fully Connect Feedforward Network）

 2、矩阵运算（Matrix Operation）

 3、手写数字识别案例

 step1、定义神经网络

 step2、定义损失函数

step3、选择最佳模型

 4、反向传播

---

摘要

本周学习了机器学习的基本概念和训练模型的步骤；了解了模型对参数的要求并学会了用梯度下降算法寻找最小损失点；学习了线性模型和非线性模型的表示方法，并学习了两种激活函数，Sigmoid 和 ReLU ；初步了解了神经网络和深度学习，了解了深度学习的训练步骤；最后还学习了反向传播方法。

Abstract

This week, we learned the basic concepts of machine learning and the steps for training models; we understood the requirements for model parameters and learned to use the gradient descent algorithm to find the minimum loss point; we learned about the representation methods of linear models and nonlinear models, and studied two activation functions, Sigmoid and ReLU; we had a preliminary understanding of neural networks and deep learning, and learned about the training steps of deep learning; finally, we also learned about the backpropagation method. 

一、机器学习的基本概念

机器学习就是使机器具有学习能力，具体来说就是使机器能够找出若干合适的函数，根据给定的输入，通过机器学习得出的函数的计算，输出特定的结果。这样的函数在深度学习中叫做神经元，其输入输出为：

• 输入：可以是向量、矩阵和序列等。
• 输出：可以是数值、类别（分类的结果）、文本、图片等。

机器学习的任务

• Regression:回归，输出结果为数值型。

例如：根据今天的某些数据来预测明天的某项数值

•  Classification:分类，机器从给定的若干类别中选择它认为可能性最大的一个类别输出。

例如：需要预测下一步棋子的位置，是一个分类问题，棋盘的每个可以落子的位置都是一个类别，机器需要从这些类别中选择一个类别，也就是位置来输出

• Structured Learning :输出有结构的东西，让机器学会创造，如画图、写文章等。

二、机器找模型的方法

现抛出一个问题，假设在某平台上（如B站），某创作的过往后台数据都已知，能否通过这些数据来预测明天的数据？

由以上问题来引出机器找函数的方法

1、定义一个带有未知参数的函数

根据自己的知识和经验，先按自己的猜测人为定义出一个带有未知参数的函数，这个猜测的函数不一定是好的，但是没关系，先定义出来。

以上初步定义了一个简单的线性函数来根据前一天的浏览量来预测后一天的浏览量，其中b和w为未知参数，需要在后续根据已知的数据来确定其取值，y是预测值，即预测的后一天的浏览量。

上式的函数在机器学习中称为模型，x1是特征，是来自于已知数据，即前一天的浏览量，w为权重（weight）,b偏差（bias）

2、定义损失函数 

损失是真实值与预测值之间的差距

 损失函数的输入是一组 (b,w)，输出是取当前w和b的模型带来的损失，即预测值与真实值的差距，损失函数的输出可以反映当前的(b,w)的好坏程度，损失越大，参数越差，损失越小，参数越好。

 举个直观的例子：假如当前的(b,w)的取值为（0.5k,1),损失函数为 L(b,w),则：

 在训练集（已知数据）中计算损失：

其中y为预测值，为数据中的真实值。 

根据2017年1月1日的数据用模型预测后一天的浏览量为5.3k,而真实数据为4.9k，二者不一致，这就有了损失，这里选择的单个损失计算方法为绝对误差：

由此算得损失值e1为 0.4k，同理依次计算e2,e3...

 根据每天的单个损失值来计算总损失值 Loss，Loss 越大，代表现在的参数越差，如用取平均值法计算Loss:

上式中N为训练样本的个数 ，即n的最大取值。

Loss 函数是自定义的，每个任务所适合的 Loss 可能不一样，MAE 和 MSE 是两种常见的求 e 的方法：

 3、最佳化

所谓最佳化，就是找一组能够使得 Loss 输出最小的参数（b,w），记为（b*,w*），（b*,w*）是最好的一组参数

用 Gradient Descent（梯度下降）的方法来寻找b*,w*。

为了理解梯度下降算法，先看一个参数的情形：假设函数L是关于w的参数，L(w)

 

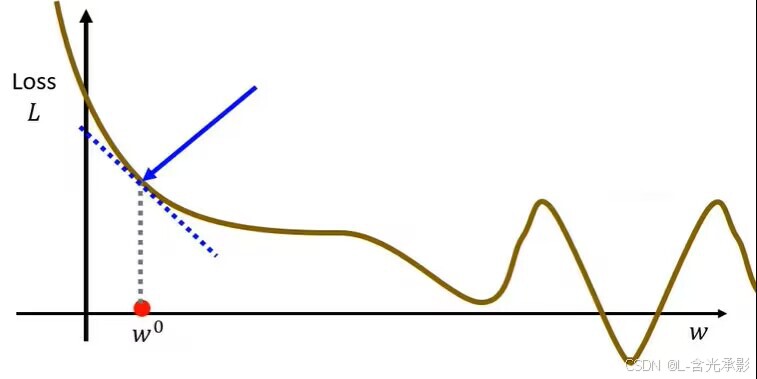
这里用梯度下降算法可能得到的是局部最小值，但这个问题并不难解决，在后续学习 

 由以上L(w)的梯度下降计算方法可以推广 L(w,b) 的梯度下降的计算方法：

 根据上面的Error Surface图可以直观看到双参函数的梯度下降算法对参数的更新过程，图中颜色越鲜艳的位置表示损失越大。

以上三个步骤加起来是机器学习的训练过程，针对的数据只是已知的数据（训练集）。而机器学习的任务是要预测未知的数据，所以现在拿已训练好上的模型来进行预测任务，结果如下图所示

<