哈希表（散列表）

本文参考《大话数据结构》

哈希表的定义

我们希望查找数据，能够像访问数组那样，能够随时随地的查找到第几个元素。也就是希望能够给一个关键字，查找的它的时间是o(1)

也就是说，我们需要通过某个函数f，使得

通过这样的转换，我们就不需要通过关键字进行比对寻找，直接通过位置寻找。使得关键字和存储位置一一对应。有点儿像python中的字典。

哈希表查找的步骤

1. 通过散列函数计算散列地址。

2. 查找时通过散列函数记录的地址，按照散列地址访问记录。

散列技术既是一种存储方法，又是查找方法

哈希函数的构造方法

首先构造一个哈希函数。那么如何构造一个比较好的哈希函数呢。

1. 计算简单，散列表的计算时间尽量简单

2. 散列地址分布均匀

直接定址法

比如说统计年龄0~100岁的人口数字，直接用年龄作为关键字查找。通常其哈希函数为线性

$$
f(key) = a*key+b
$$

数字分析法

抽取数字的关键部分进行截取，然后计算存储位置

平方取中法

假设关键字为1234，它的平方为1522756，再抽取中间的3位数，就是227.适合不知道关键字的分布，而位数又不大。

折叠法

将关键字从左到右分割成位数相等的几部分（最后一个不部分不够可以短些)

除留余数法

$$
f(key) = key \quad mod \quad p (p<<m)
$$

假如我们有个12条记录表，我们就用法f(key)mod12,例如29mod12=5

下标	0	1	2	3	4	5	6	7	8	9	10	11
关键字	12	25	38	15	16	29	78	67	56	21	22	47

根据经验，p为小于或等于表长的最小质数或不包含小于20质因子的合数

随机数法

选择一个随机数，随机函数为它的散列地址f(key)=random (key)

散列冲突的方法

开放定址法（线性探测法）

一旦发生了冲突，就去寻找下一个空的散列地址。

$$
f_i(key)=(f(key)+d_{i})\quad mod\quad m(d_i=1,2,3,4,m-1)
$$

比如说我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,34}，表长为12,。我们散列函数f(key)=key mod 12

下标	0	1	2	3	4	5	6	7	8	9	10	11
关键字	12	25			16			67

key=37时，f(37)=1,与25所在的位置冲突。f(37)=(f(37)+1) mod 12 =2将其存入2的位置

下标	0	1	2	3	4	5	6	7	8	9	10	11
关键字	12	25	37		16			67

key=48时，我们计算得到f(48)=0,与12冲突，f(48)=(f(48)+1)mod12 =1 还冲突，我们一直重复。直到没有发生冲突。

二次探测法

下标	0	1	2	3	4	5	6	7	8	9	10	11
关键字	12	25	37	15	16	29	48	67	56		22	47

我们会发生以下情况，34与22发生冲突，可是后面的没有地址了。为了不让关键字都聚集在某一块区域。我们称这种方法为二次探测法。

$$
f_i(key)=(f(key)+d_i)\quad mod m(d_i=1^2,-1^2,2^2,-2^2,..,q^2,-q^2,q<<m/2)
$$

再散列函数法

我们事先准备多个散列函数

$$
f_i(key)=RH_i(key)(i=1,2,...k)
$$

$$
RH_{i} 就是不同的散列函数
$$

每当发生一个冲突时换一个散列函数

链地址法

 

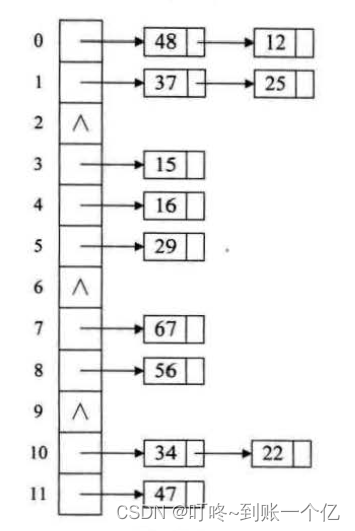
散列表的实现

#define unsuccess 0
#define Hashsize 12  //定义表长的长度
#define INIT 0
#include<stdio.h>
#include<stdlib.h>
typedef struct {
    int* elem; //数据元素存储基址，动态分配数组
    int count; //当前数据元素的个数
}HashTable;
​
int m = 0; //散列表长，全局变量
​
/*初始化散列表*/
void InitHashTable(HashTable* H) {
    int i;
    m = Hashsize;
    H->count = m;
    H->elem = (int*)malloc(m * sizeof(int));
    for (i = 0; i < m; i++)
        H->elem[i] = INIT;
}
​
/*散列函数*/
int Hash(int key) {
    return key % m; /*除留余数法*/
}
​
/*插入关键字进行散列表*/
void InsertHash(HashTable* H, int key) {
    int addr = Hash(key); //求散列地址
    while (H->elem[addr] != 0)  //如果不空，则冲突
        addr = (addr + 1) % m;  //开放定址法的线性探测
    H->elem[addr] = key;   //直到有空位后插入关键字
}
​
​
/*散列表查找关键字*/
int  SearchHash(HashTable H,int key, int* addr) {
    *addr = Hash(key); //求散列地址
    while (H.elem[*addr] != key)
    {
        *addr = (*addr + 1) % m;//开放地址法的线性探测
        if (H.elem[*addr] == 0 || *addr == Hash(key))
        {
            return 0;//说明关键字不存在
        }
    }
    return 1;
}