
a显示了一个单顶点四折痕的图,其中包含四个面板或扇区 1 到 4,以及四个折痕 A、B、C 和 D;四个折痕在公共点 O 处相交。相邻折痕之间的四个扇形角是α12、α23、α34和α41;相邻扇区之间的四个二面角为θ1、θ2、θ3和θ4。从机制的角度来看,通过将扇区作为链接,将折痕作为旋转关节,可以获得等效的球形 4R 连接,如图(b) 所示;其中扇区 1 到 4 成为链接 1 到 4,折痕 A 到 D 成为旋转关节A1到 A4和 二面角α12、α23、α34和α41成为连杆的扭转角。因此,球形 4R 连杆的运动学可以应用于 4 阶折纸顶点运动学分析。
在图b中,遵循d-H约定,坐标系Fi建立在连杆机构的关节处。其中,Zi轴(i= 1、2、3 和 4)沿关节 Ai的关节轴;Xi轴垂直于Zi和Zi+1 (Xi = Zi×Zi+1)(需要注意的是,当下标 i + 1 = 5 时,它被替换为 1);Yi轴 可以使用右手定则和原点 Oi与点 O 重合。角度θi+1定义为从Xi轴 到Xi+1-i轴,关于Zi+1轴的角度;角度αi(i +1)是 扭转角度Zi和Zi+1关于Xi的角度(当 i + 1 = 5 时,它被替换为 1)。此外,链路长度 ai(i +1)定义为沿Xi ,Zi到Zi+1的距离;di+1定义为沿Zi+1Xi到Xi+1的距离.对于球形 4R 连杆,由于所有四个旋转关节都在一个公共点 O 处相交,因此它有一个a12= a23= a34= a41= 0 和 d1= d2= d3= d4= 0 的 值,因为坐标系之间没有平移。
两个相邻的关节角度θi和θi+1,例如θi作为输入,另一个即θi+1作为输出,则根据循环方程 R12R23R34R41= I 其中Rij 是旋转矩阵,I 是 3 × 3 单位矩阵,两个相邻关节角之间的一般关系可以表示为
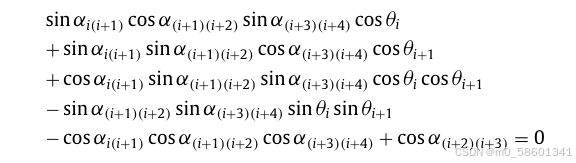
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








