本文深入探讨了算法与数据结构中的关键概念，包括冒泡排序、选择排序、插入排序的效率比较，以及位运算如与(&)、或(|)、异或(^)的规则和应用。通过实例展示了如何使用位运算交换数值和找出数组中奇数次出现的数字。此外，文章还讲解了递归排序如快速排序和归并排序的实现，并讨论了递归和Master公式在算法复杂度分析中的作用。
算法与数据结构
对数器
通过生成随机数，讲所有随机数完全拷贝下来。总共生成两份完全一样的随机数。后分别输入两种方法里面。（可以动态调节输入数据的多少）
for (int i = 0; i < testTime; i++) {
int[] arr1 = generateRandomArray(maxSize, maxValue);
int[] arr2 = copyArray(arr1);
insertionSort(arr1);
comparator(arr2);
if (!isEqual(arr1, arr2)) {
succeed = false;
break;
}
}
System.out.println(succeed ? "Nice!" : "Fucking fucked!");
认识复杂度
异或运算
与运算符（&）
运算规则：
0&0=0；0&1=0；1&0=0；1&1=1
即：两个同时为1，结果为1，否则为0
例如：3&5
十进制3转为二进制的3：0000 0011
十进制5转为二进制的5：0000 0101
------------------------结果：0000 0001 ->转为十进制：1
即：3&5 = 1
或运算（|）
运算规则：
0|0=0； 0|1=1； 1|0=1； 1|1=1；
即 ：参加运算的两个对象，一个为1，其值为1。
例如：3|5 即 00000011 | 0000 0101 = 00000111，因此，3|5=7。
异或运算符（^）
运算规则：0^ 0=0； 0^ 1=1； 1^ 0=1； 1^1=0；
即：参加运算的两个对象，如果两个位为“异”（值不同），则该位结果为1，否则为0。（相同为零不同为一------类似于无进位相加）
例如：3^ 5 = 0000 0011 | 0000 0101 =0000 0110，因此，3^5 = 6
例子一：
交换两个数：
public class a {
public static void main(String[] args) {
int a=1;
int b=2;
a=a^b;
b=a^b;
a=a^b;
System.out.println(a+" "+b);
}
}
输出结果：
注意：a和b必须指向两块内存，如果指向同一位置，会把这个位置置为零。
例子二：
在一个数字中，只有一种数出现了奇数次，其他所有数都出现了偶数次。
public class a {
public static void main(String[] args) {
int []a={1,1,2,3,3};
int ero=0;
for(int i=0;i<a.length;i++){
ero=ero^a[i];
}
System.out.println(ero);
}
}
输出结果：
在一个数字中，只有两种数出现了奇数次，其他所有数都出现了偶数次。
public class a {
public static void main(String[] args) {
int []a={1,1,2,3,3,4 };
int ero=0;
for(int i=0;i<a.length;i++){
ero^=a[i];
}
int rightOne=ero&(~ero+1);//取出最右面的1
int one=0;
for(int i:a){
if((i & rightOne)==0){
one^=i;
}
}
System.out.println(one+" "+(one^ero));
}
}
输出结果：
排序
十大排序算法详解（一）冒泡排序、选择排序、插入排序、快速排序、希尔排序
冒泡排序：最笨的排序
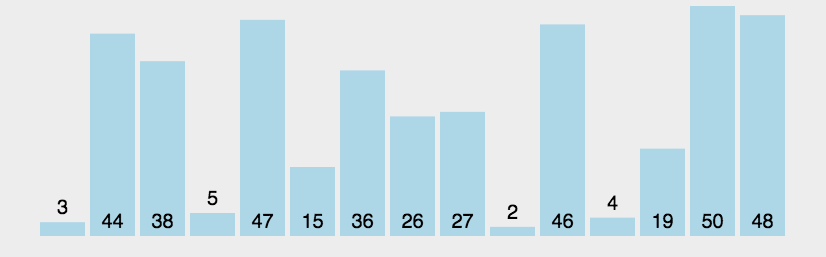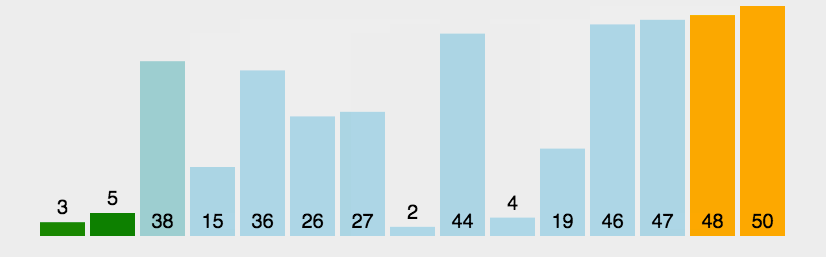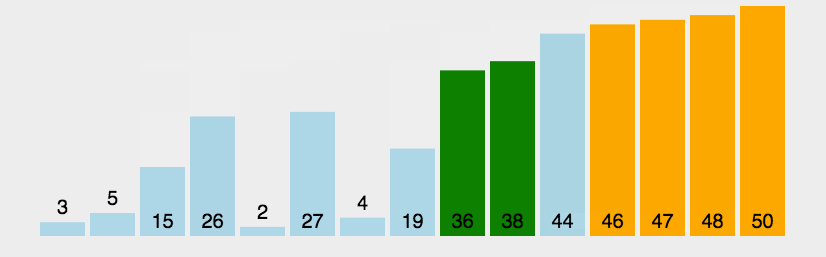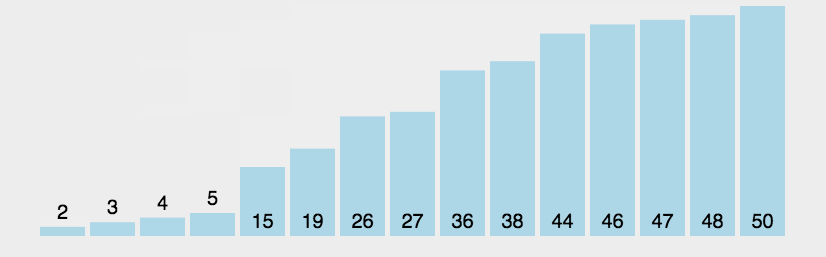
public class a {
public static void main(String[] args) {
int[] a = {5, 4, 3, 2, 1};
for(int i=0;i<a.length;i++){//0--i是有序的
for(int j=0;j<a.length-1-i;j++){
if(a[j]>a[j+1]){
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
for(int i:a){
System.out.print(i+" ");
}
}
}
输出结果：
选择排序
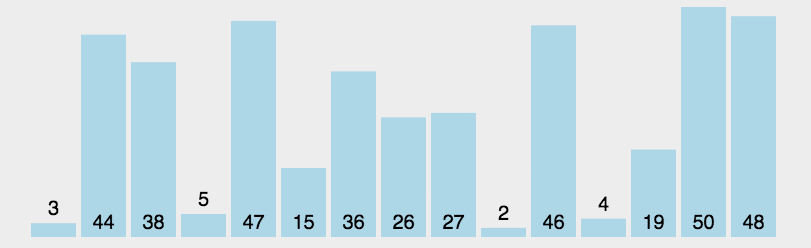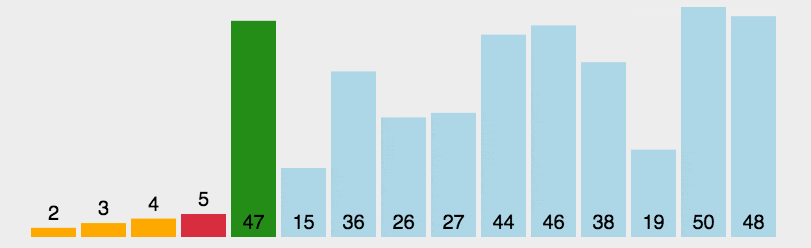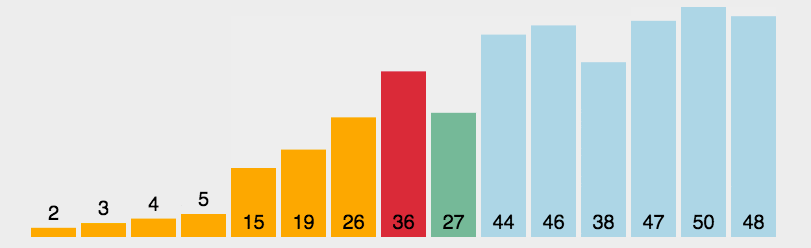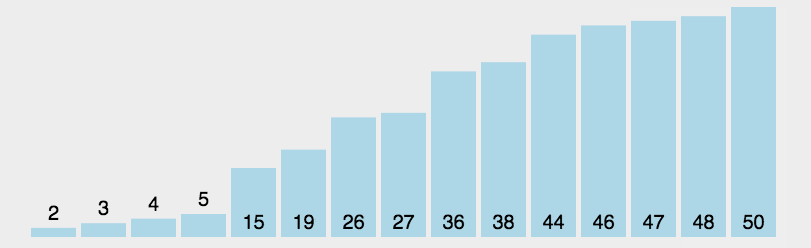
public class a {
public static void main(String[] args) {
int[] a = {5, 4, 3, 2, 1};
for(int i=0;i<a.length;i++){
int min=i;
for(int j=i+1;j<a.length;j++){
if(a[j]<a[min]){
int temp=a[j];
a[j]=a[min];
a[min]=temp;
}
}
}
for(int i:a){
System.out.print(i+" ");
}
}
}
输出结果：
插入排序：经过综合的比较，插排比冒泡和选择更快
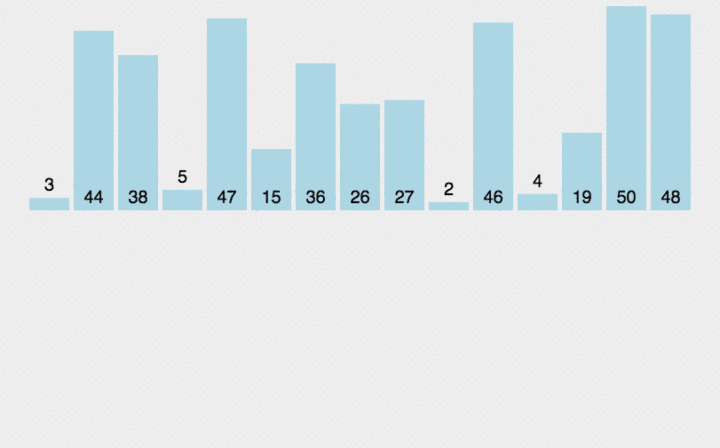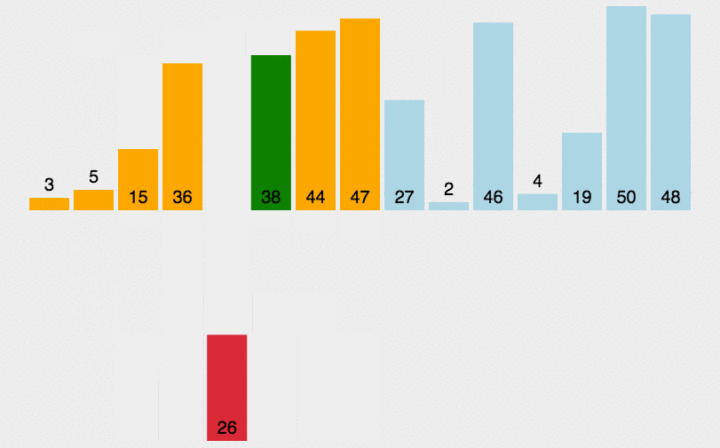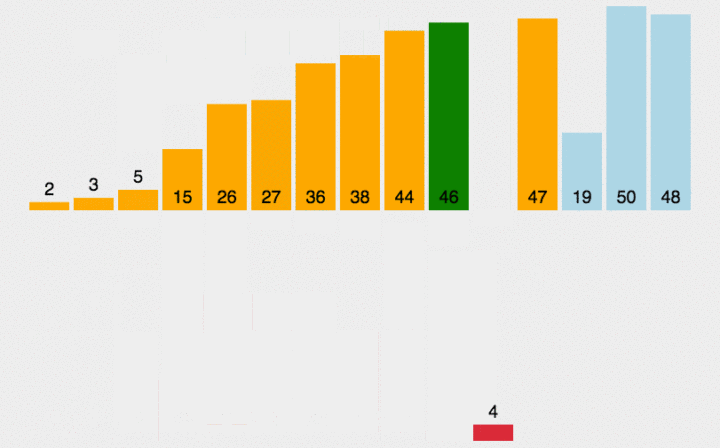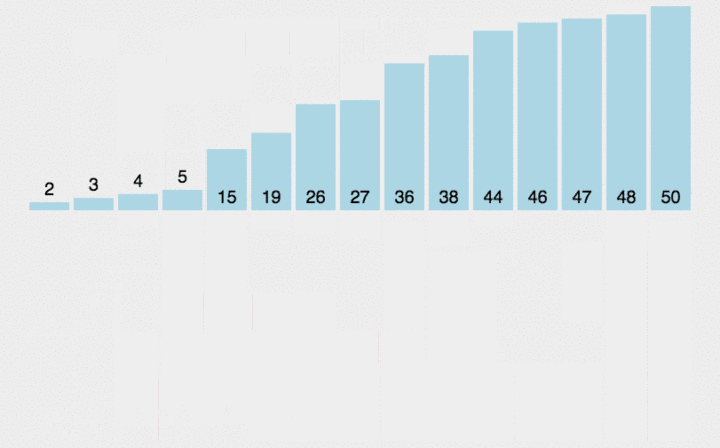
public class a {
public static void main(String[] args) {
int[] a = {5, 4, 3, 2, 1};
for(int i=1;i<a.length;i++){//0--i是有序的
for(int j=i-1;j>=0&&a[j]>a[j+1];j--){
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
for(int i:a){
System.out.print(i+" ");
}
}
}
递归排序
先让左边排序，然后让右面排序。最后让整体就行排序。时间复杂度O(N*log(N)),额外空间复杂度O(N)
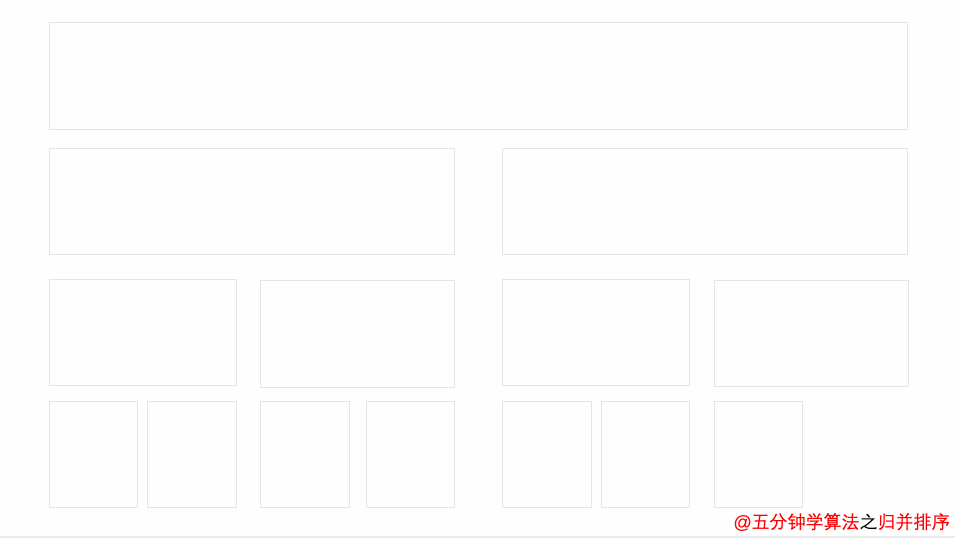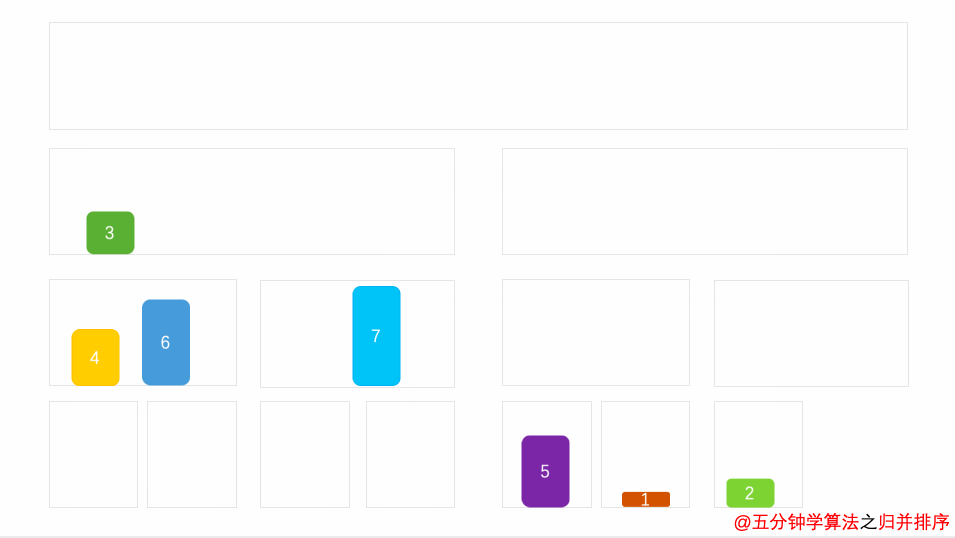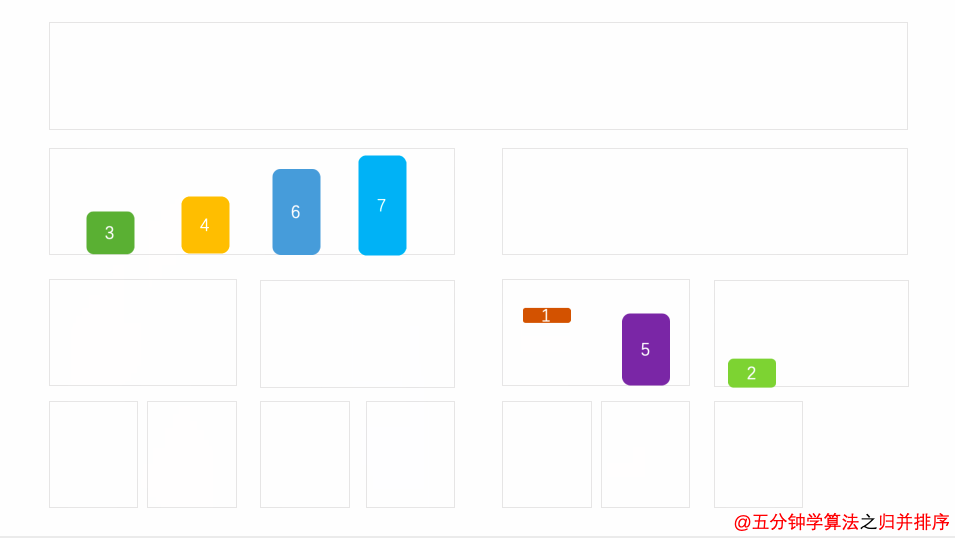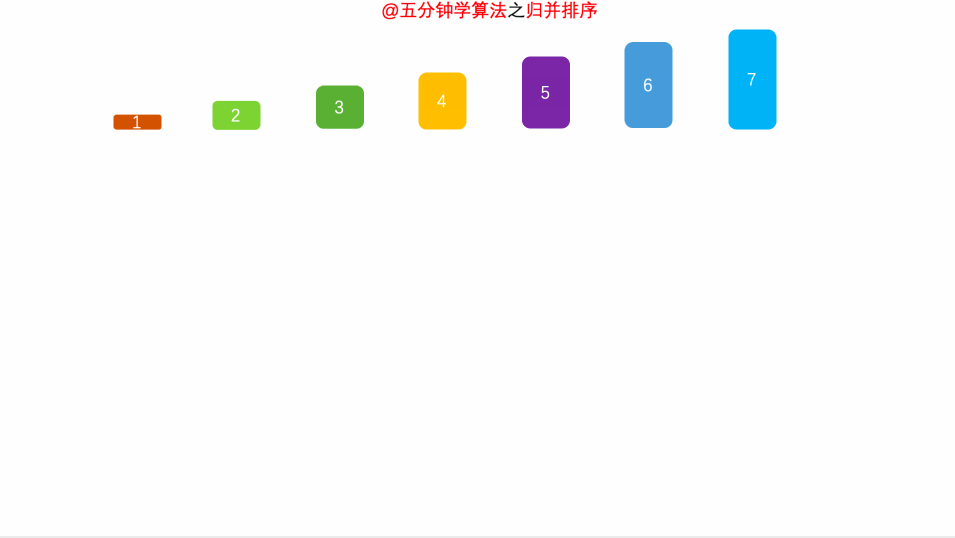
图片转自：博客园的五分钟学算法
链接地址：分而治之的归并排序
public class a {
public static void mergeSort(int[] arr, int l, int r) {
if (l == r) {//左边界和右边界重合，说明已经仅剩一个元素
return;
}
int mid = l + ((r - l) >> 1);
mergeSort(arr, l, mid);//递归左面部分
mergeSort(arr, mid + 1, r);//递归右面部分
merge(arr, l, mid, r);//进行比较
}
public static void merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
while (p1 <= m && p2 <= r) {
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
}
public static void main(String[] args) {
int []a={5,4,3,2,1};
mergeSort(a,0,a.length-1);
for(int i:a){
System.out.println(i);
}
}
}
输出结果：
快排
在一组数中通过random()方法，随机取一个位置记录这个位置的特定数num，将大于该数小于该数和等于这个数放在三块区域。将比特定数小的从左到右扩张，比特定数大的从右到左扩张。从左到右进行遍历：如果a[i]<num，a[i]和小于区的下一个交换，小于区向右扩，进行i++。如果a[i]==num，，等于区向右扩，进行i++。如果a[i]>num，a[i]和大于区的前一个交换，大于区向右左扩，i不变。
图解：
public class a {
public static void quickSort(int[] arr, int l, int r) {
if (l < r) {
swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
int[] p = partition(arr, l, r);
quickSort(arr, l, p[0] - 1);
quickSort(arr, p[1] + 1, r);
}
}
public static int[] partition(int[] arr, int l, int r) {
int less = l - 1;
int more = r;
while (l < more) {
if (arr[l] < arr[r]) {
swap(arr, ++less, l++);
} else if (arr[l] > arr[r]) {
swap(arr, --more, l);
} else {
l++;
}
}
swap(arr, more, r);
return new int[] { less + 1, more };
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int []a={1,2,3,4,5};
quickSort(a, 0, a.length - 1);
for(int i:a){
System.out.println(i);
}
}
}
递归
简单说就是自己调用自己。
master公式
满足master公式：T [n] = a*T[n/b] + O (N^d)），时间复杂度如下：
- 当d<logb a时，时间复杂度为O(n^(logb a))
- 当d=logb a时，时间复杂度为O((n^d)*logn)
- 当d>logb a时，时间复杂度为O(n^d)
递归的一经典问题：
- 求小和问题：大致意思就是 一个数的前面比他小就求和，最后所有和累加到一起。举个例子： 1，2，3，4，5。 2的前面有个1比2小，所以在本列数中2的小和就是1。3的前面有1和2都比他小，所以在本列数中3的小和就是1+2=3。以此类推这列数的小和是1+3+6+10=20。
题解：看似叙述过程很难，但是不妨我们逆着想一下。1被加了4次，2被加了3次，3被加了2次，4被加了1次。所以可得14+23+32+41=20。显然这种思想比传统的遍历复杂度要更低。复杂度为：O(N*log(N))。
采用递归的思想进行解决，把他们用递归分成很多组，直至分成单个元素。在计算时，同组的数据不进行比较，不同的组之间进行比较。后有序集合到一个数组中。（这样既可以保证不漏掉每一次运算，也不多重复进行运算过的数据）。
代码解释:
递归拆开后的运算：
public class a {
public static int smallSum(int[] arr) {
return mergeSort(arr, 0, arr.length - 1);
}
public static int mergeSort(int[] arr, int l, int r) {
if (l == r) {
return 0;
}
int mid = l + ((r - l) >> 1);
return mergeSort(arr, l, mid)
+ mergeSort(arr, mid + 1, r)
+ merge(arr, l, mid, r);
}
public static int merge(int[] arr, int l, int m, int r) {
int[] help = new int[r - l + 1];
int i = 0;
int p1 = l;
int p2 = m + 1;
int res = 0;
while (p1 <= m && p2 <= r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
while (p1 <= m) {
help[i++] = arr[p1++];
}
while (p2 <= r) {
help[i++] = arr[p2++];
}
for (i = 0; i < help.length; i++) {
arr[l + i] = help[i];
}
return res;
}
public static void main(String[] args) {
int []a={1,2,3,4,5};
int sum=smallSum(a);
System.out.println(sum);
}
}
算法中一些注意的细节：
当计算数字中两个值的中点时推荐使用mid=l+(r-l)>>1。如果用传统的方式当左右范围很大时可能会越界。举例说明：
public static void main(String[] args) {
int x = 1999999998;
int y = 1999999998;
int mid = (x+y) / 2;
int mid2 = x + (y-x) / 2;
System.out.println(mid); //-147483650
System.out.println(mid2); //1999999998
}
因为int的范围是[-2^31 – 2^31-1],但是1999999998+1999999998已经超过int的最大范围
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
