在取模运算中 有如下定理:
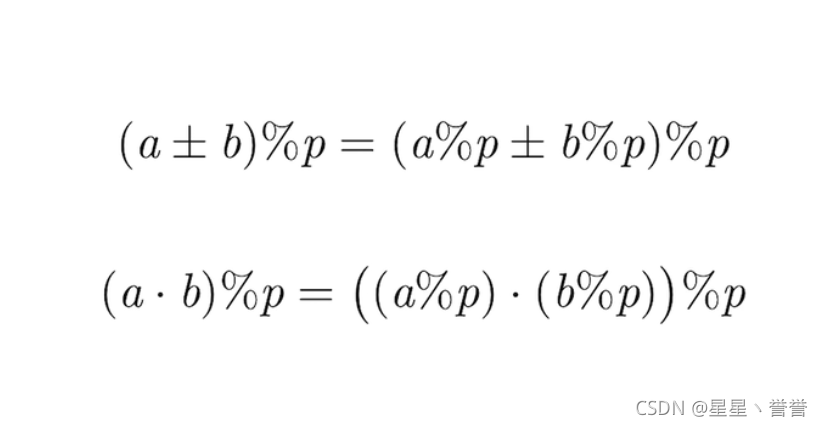 注意:在加法运算中要注意最后结果可能为负数,所以要在最后加上要取模的数;
注意:在加法运算中要注意最后结果可能为负数,所以要在最后加上要取模的数;
上述定理只在乘法和加法中有效,在除法中一般是无效的
所以在运算中引入了逆元运算
在计算 a/b = x(mod p) 中 并不等于 (a%p) / (b%p) = x;
但是在运算中可能数字比较大,必须将a取模 这时引入了逆元
怎么实现呢 就是将除法转化为乘法 即 将a/b = a *(b的逆元) = x(mod p);
这里需要注意的是 逆元并不是一定存在的 ,简单证明 、
a/b = x(mod p) 式①
a * b(逆) = x (mod p) 式②
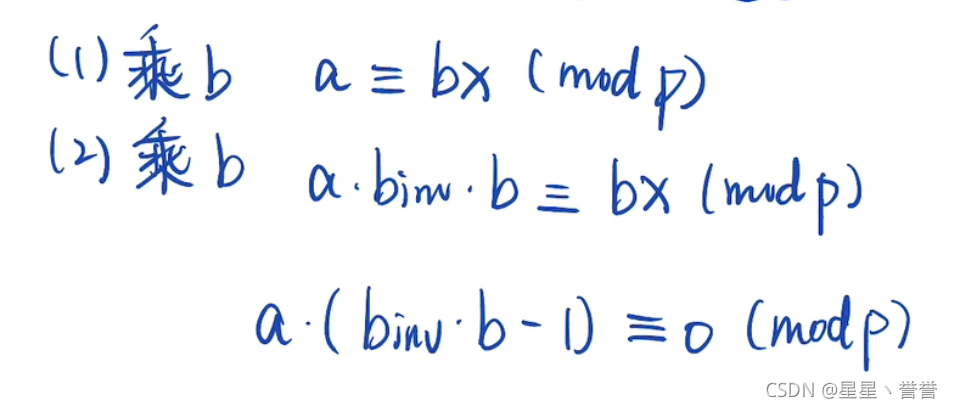
b (逆) * b = 1(mod p);
怎么求逆元呢
如果两个数互素则:
根据费马小定理 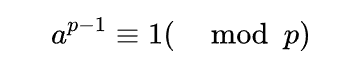
当p为质数时 a 的逆元为a的p-2次
可以由快速幂算法求得;




 本文探讨了取模运算中的定理,包括加法负数处理和乘法逆元概念。重点讲解了如何通过费马小定理快速求得互素数的逆元,并演示了如何将除法转换为乘法来简化大数计算。
本文探讨了取模运算中的定理,包括加法负数处理和乘法逆元概念。重点讲解了如何通过费马小定理快速求得互素数的逆元,并演示了如何将除法转换为乘法来简化大数计算。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








