RMSNorm

 1、RMSNorm

        RMSNorm 则不涉及均值和⽅差的计算，⽽是通过均⽅根（Root Mean Square, RMS）来进⾏规范化。其核⼼思想是基于输⼊的幅值（magnitude），⽽不依赖于其均值。

2、LayerNorm

        LayerNorm 是⼀种⼴泛应⽤于神经⽹络中的正则化技术，主要⽤于稳定深层⽹络的训练，避免梯度消失或爆炸。它通过对输⼊进⾏均值和⽅差归⼀化来标准化每⼀层的激活。

3、RMSNorm和LayerNorm对比

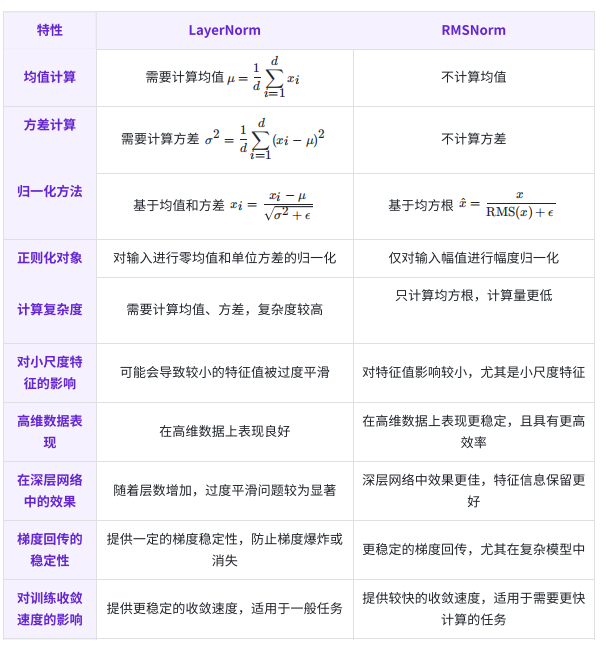
4、二者有效性分析

        LayerNorm 通过均值归零和⽅差归⼀化，确保数据的平均值为 0，标准差为 1。这在某些情况下有助于稳定训练，但并不总是必要。对数据的均值偏移并不是所有任务的关键。例如，在⼀些任务中，输⼊数据的幅值⼤⼩（即输⼊的整体能量）可能⽐相对位置（即偏移量）更为重要。

        RMSNorm 通过均⽅根来标准化幅度，消除对输⼊数据的过度缩放，⽽不会⼲扰数据的相对位置或特征。这样做的优势是，它保持了输⼊的特征分布结构，但调整了输⼊的整体尺度。对于⼀些深度⽹络，尤其是⾃注意⼒机制（如 Transformer 结构）中，这种幅度归⼀化在不破坏输⼊特征的情况下，有助于提⾼模型的训练效果。

        特定任务不需要零均值： 并不是所有任务都需要输⼊数据有零均值。例如，在⼀些计算过程中（如神经⽹络的某些层或处理⾼维数据时），数据的幅度变化对模型更为重要，而数据相对于均值的偏移则⽆关紧要。因此，RMSNorm 通过幅值归⼀化来控制数据在⼀定范围内波动，不必通过均值归零。

总结

        LayerNorm 和 RMSNorm 都是有效的正则化方法，但它们在核心的计算⽅式和应用场景上有所不同：

• LayerNorm 更适合处理均值与方差对特征影响较大的任务，特别是⼩批量数据和 NLP 任务中。

• RMSNorm 则适⽤于幅度归⼀化为主、特征幅度较⼤的场景，如深层神经⽹络或⾼维数据中，同时它的计算效率也更⾼。