JAVA高级排序——希尔排序

        为何称高级排序呢？是因为之前学习的基础排序，包括冒泡排序，选择排序还有插入排序，对他们在最坏情况下的时间复杂度做了分析，发现都是O(N^2)，而平方阶通过我们之前学习算法分析我们知道，随着输入规模的增大，时间成本将急剧上 升，所以这些基本排序方法不能处理更大规模的问题，接下来我们学习一些高级的排序算法，争取降低算法的时间 复杂度最高阶次幂。

希尔排序

希尔排序是插入排序的一种，又称“缩小增量排序”，是插入排序算法的一种更高效的改进版本。

        学习插入排序的时候，我们会发现一个很不友好的事儿，如果已排序的分组元素为{2,5,7,9,10}，未排序的分组 元素为{1,8}，那么下一个待插入元素为1，我们需要拿着1从后往前，依次和10,9,7,5,2进行交换位置，才能完成真 正的插入，每次交换只能和相邻的元素交换位置。那如果我们要提高效率，直观的想法就是一次交换，能把1放到 更前面的位置，比如一次交换就能把1插到2和5之间，这样一次交换1就向前走了5个位置，可以减少交换的次数。

需求：

排序前：{9,1,2,5,7,4,8,6,3,5}

排序后：{1,2,3,4,5,5,6,7,8,9}

排序原理：

1.选定一个增长量h，按照增长量h作为数据分组的依据，对数据进行分组；

2.对分好组的每一组数据完成插入排序；

3.减小增长量，最小减为1，重复第二步操作。

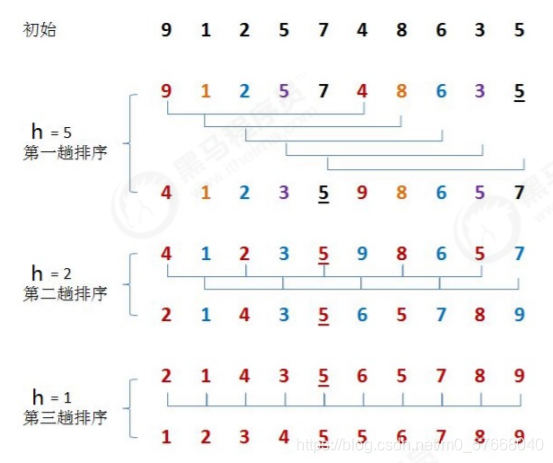
 解释一下：

先将原数据分组，对每一组数据进行插入排序

增长量h就是对原数据分组用的，h＝5：索引0和索引5为一组，索引1和索引6为一组......

第一趟排序：h＝5：索引0和索引5：我们认为索引0处元素9为默认排序好的，待排序的就是元素4，元素4比元素9小，交换位置；同理元素5（索引3）和元素3（索引8）交换，元素7（索引4）和元素5（索引9）交换。得到（4、1、2、3、5、9、8、6、5、7）

第二趟排序：减小h，h＝2：索引0、2、4、6、8处的元素为一组，索引1、3、5、7、9又为一组。分别对这两组数据进行插入排序：分别得到的元素为：（2、4、5、5、8）和（1、3、6、7、9），最终结果为（2、1、4、3、5、6、5、7、8、9）

第三趟排序：减小h，h最小为1：每个元素为一组，进行插入操作，完成排序。

增长量h的确定：增长量h的值每一固定的规则，我们这里采用以下规则：

        int h=1;
        while(h<N/2){
            h=h*2+1;
        }
//循坏结束我们就可以确定h的最大值
h的减小规则为：
        h=h/2;

希尔排序的API设计：

类名	Shell
构造方法	Shell()：创建Shell对象
成员方法	1.public static void sort(Comparable[] a)：对数组内的元素进行排序 2.private static boolean greater(Comparable v,Comparable w):判断v是否大于w 3.private static void exch(Comparable[] a,int i,int j)：交换a数组中，索引i和索引j处的值

public class Shell {
    /*
对数组a中的元素进行排序
*/
    public static void sort(Comparable[] a){
        int N = a.length;
    //确定增长量h的最大值
        int h=1;
        while(h<N/2){
            h=h*2+1;
        }
//当增长量h小于1，排序结束
        while(h>=1){
//找到待插入的元素
            for (int i=h;i<N;i++){
//a[i]就是待插入的元素
//把a[i]插入到a[i-h],a[i-2h],a[i-3h]...序列中
                for (int j=i;j>=h;j-=h){
//a[j]就是待插入元素，依次和a[j-h],a[j-2h],a[j-3h]进行比较，如果a[j]小，那交换位置，如果不小于，a[j]大，则插入完成。
                    if (greater(a[j-h],a[j])){
                        exch(a,j,j-h);
                    }else{
                        break;
                    }
                }
            }
            h/=2;
        }
    }
    /*
    比较v元素是否大于w元素
    */
    private static boolean greater(Comparable v,Comparable w){
        return v.compareTo(w)>0;
    }
    /*
    数组元素i和j交换位置
    */
    private static void exch(Comparable[] a,int i,int j){
        Comparable t = a[i];
        a[i]=a[j];
        a[j]=t;
    }
}

希尔排序的时间复杂度分析

在希尔排序中，增长量h并没有固定的规则，有很多论文研究了各种不同的递增序列，但都无法证明某个序列是最好的，对于希尔排序的时间复杂度分析，已经超出了我们课程设计的范畴，所以在这里就不做分析了。

我们可以使用事后分析法对希尔排序和插入排序做性能比较。