CRF模型

最新推荐文章于 2025-04-17 09:00:00 发布
最新推荐文章于 2025-04-17 09:00:00 发布
阅读量3.4k 收藏 34
点赞数 18
文章标签： 大数据
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_57332527/article/details/125662132
版权

目录

隐马尔可夫模型HMM（这里用一个HMM第三个问题来举例）

CRF条件随机场

 马尔可夫性：

概率无向图：

团和最大团：

概率无向图的因子分解：

CRF的应用

总结

3.1 随机场->马尔可夫随机场

3.2 马尔可夫随机场->条件随机场

3.3 条件随机场->线性链条件随机场注意在 CRF 的定义中，我们并没有要求 X 和 Y 有相同的结构。

隐马尔可夫模型HMM（这里用一个HMM第三个问题来举例）

简单来说第一天的初始状态未知，但是状态转移矩阵已知。当天伴随自变量的事件状态转移矩阵已知，同时知道一段时间的因变量的结果，求这段时间概率最大的自变量

 以上是一个生动的例子

要解决这个问题：需要使用viterbi算法

介绍viterbi算法就不用上面的例子了，换一个例子进行通俗讲解：

 这是一个取球不放回模型，pai是初始条件概率矩阵，A是状态转移矩阵，B是观测状态转移矩阵，由每日状态来决定，简单理解就是一个随当天自变量而生成的因变量。知道三次取球结果为红白红，试问三次取球分别从哪个箱子取出的概率最大。

初始条件概率矩阵已知，则根据观测状态转移矩阵计算出即首日观测红球概率矩阵。首次取球，从取到第一个箱子且红球概率为0.1，同理2红0.16，3红0.28，如果首次是这样的条件矩阵， 那么可以推算出第二次在各个箱子开出白球的概率（这里是在第一次开红球的基础上在各箱中开白球的概率）

 需要注意的是，因为第二次在第一个箱子里面开白球的概率是由第一次在三个箱子开红球这个事件共同决定，我们找出第一次在三个箱子中最有可能的哪一个，也就是在式子中的max函数，同理得到第二次每个箱子开白球所最有可能的第一次开红球的箱子都是3，可以大致觉得第一次就是由三这个箱子开出的红球；同理第三次开红球推测第二次由哪个箱子开白球的概率更大，前两个箱子中开红球认为由二箱子开白球概率大，第三箱子开红球认为由三箱子开白球概率大，这里取第三个箱子的观点是由于第三个箱子开出红球而且在取第三个箱子条件概率下大于前两个之和，所以认为第二次取的是第三个箱子，而第三次取的是什么箱子就是看第三次哪个取红球的概率大，这就构成了整条链的概率，比穷举法节约了时间复杂度。

CRF条件随机场

P(Y/X)  ：X是输入变量，Y是输出变量，Y满足马尔可夫随机场。

条件概率：略

无向图--概率无向图模型：马尔可夫随机场

条件随机场：在X输入下Y输出满足马尔可夫条件

线性链的条件随机场：X是线性所产生的Y是马尔可夫随机场

概率图模型：（状态转移的图）

 马尔可夫性：

概率无向图：

概率无向图本质上就是具有马尔可夫性的一个无向图

下图是一个概率无向图，具有全局马尔可夫性（局部马尔可夫性，成对马尔可夫性自行脑补）

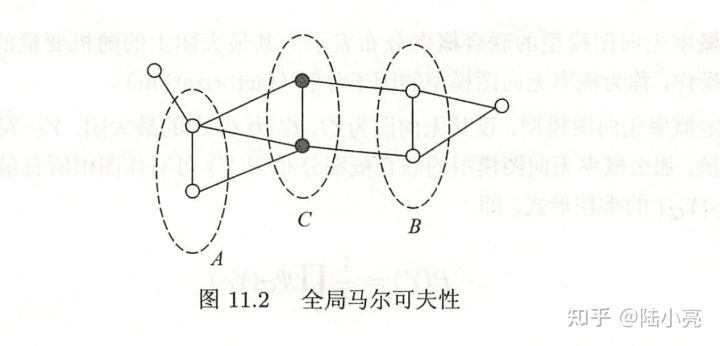
介绍重点是概率无向图可以进行因式分解，至于如何进行因式分解，就需要介绍团和最大团的概念

团和最大团：

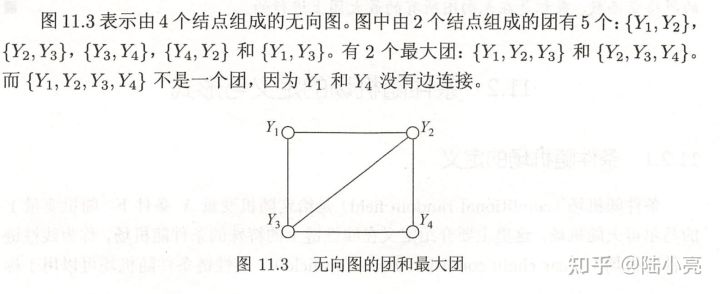
概率无向图的因子分解：

CRF的应用

输入输出经过某个分布 P(Y|X)，线性链条件随机场（Linear-CRF）公式如下
请添加图片描述

从上面那个例子，我们可以了解到，条件随机场的在 NLP 领域的作用就是：标注（或者，命名实体识别）

从公式中我们可以看到，当前的标注结果 y，还会参考上一个标注的结果 y_i-1。也就是说，CRF 在标记数据的时候，会考虑前一个数据的标记信息，这对于解析句子语法结构来说是得天独厚的优势（例如：动词后面不能跟动词）。而这一点，是普通的分类器难以做到的。
 

总结

3.1 随机场->马尔可夫随机场

首先，我们来看看什么是随机场。“随机场”的名字取的很玄乎，其实理解起来不难。随机场是由若干个位置组成的整体，当给每一个位置中按照某种分布随机赋予一个值之后，其全体就叫做随机场。还是举词性标注的例子：假如有一个十个词形成的句子需要做词性标注。这十个词每个词的词性可以在已知的词性集合（名词，动词…)中去选择。当我们为每个词选择完词性后，这就形成了一个随机场。

了解了随机场，我们再来看看马尔科夫随机场。马尔科夫随机场是随机场的特例，它假设随机场中某一个位置的赋值仅仅与和它相邻的位置的赋值有关，和与其不相邻的位置的赋值无关。继续举十个词的句子词性标注的例子：　如果我们假设所有词的词性只和它相邻的词的词性有关时，这个随机场就特化成一个马尔科夫随机场。比如第三个词的词性除了与自己本身的位置有关外，只与第二个词和第四个词的词性有关。通常一个概率无向图模型，又称为马尔可夫随机场。

3.2 马尔可夫随机场->条件随机场

CRF 是马尔可夫随机场的特例，它假设马尔科夫随机场中只有 X 和 Y 两种变量， X 一般是给定的，而Y 一般是在给定 X 的条件下的输出。这样马尔科夫随机场就特化成了条件随机场。在我们十个词的句子词性标注的例子中，X是词，Y是词性。因此，如果我们假设它是一个马尔科夫随机场，那么它也就是一个 CRF。

对于 CRF，给出准确的数学语言描述：设 X 与 Y 是随机变量，P(Y|X) 是给定 X 时 Y 的条件概率分布，若随机变量 Y 构成的是一个马尔科夫随机场，则称条件概率分布 P(Y|X) 是条件随机场。

3.3 条件随机场->线性链条件随机场
注意在 CRF 的定义中，我们并没有要求 X 和 Y 有相同的结构。

而实现中，我们一般都假设X和Y有相同的结构，即:

请添加图片描述

X和Y有相同的结构的CRF就构成了线性链条件随机场(Linear chain Conditional Random Fields,简称 Linear-CRF)
 

CRF模型详解
weixin_40103562的博客
03-04 3万+
条件随机场(CRF)是自然语言处理中的基础模型, 广泛用于分词, 实体识别和词性标注等场景. 随着深度学习的普及, BILSTM+CRF, BERT+CRF, TRANSFORMER+CRF等模型, 逐步亮相, 并在这些标注场景, 效果有显著的提升. 下面是我学习CRF的学心总结, 看了多篇知乎, paper, 和CRF++的实现代码后, 终于有了深刻的理解. 基础概念 首先, 一起看一下随机过程, 随机场, 马尔可夫随机场的定义, 在最后请出条件随机场. 随机过程: 设 ​​​​​​​TTT是一无限实数集
理解条件随机场（转）
dianwei0041的博客
07-24 2311
理解条件随机场最好的办法就是用一个现实的例子来说明它。但是目前中文的条件随机场文章鲜有这样干的，可能写文章的人都是大牛，不屑于举例子吧。于是乎，我翻译了这篇文章。希望对其他伙伴有所帮助。原文在这里[http://blog.echen.me/2012/01/03/introduction-to-conditional-random-fields/] 想直接看英文的朋...
【CRF系列】第3篇：线性链CRF详解——模型定义与参数化
熵数实验室
04-14 650
线性链CRF每个观测变量xix_ixi​都与对应位置的标签变量yiy_iyi​相连相邻的标签变量yi−1y_{i-1}yi−1​和yiy_iyi​之间有边相连图示结构如下：它保留了标签之间的相邻依赖关系（如：B-PER后面更可能是I-PER）每个标签可以利用整个观测序列的信息它的结构简单，计算效率较高。
CRF总结
weixin_33918357的博客
04-06 539
条件随机场理解 随机场理解 先从随机变量说起。 对于一个时间集合T内，每一个时间点t点，X(t)的数值都是随机的，那么X(t）称为随机过程。x(t)是依赖于时间的一组随机变量。它的分布函数叫做x（t)的一维概率分布函数。 如果有一个变量，依赖于两个时间t1,t2，就称为二维随机变量，有二维概率分布函数。-。。。。。到n维概率分布函数 两个随机过程之间的数字特征有：方差，期望，均值，协方差函数，互...
条件随机场CRF简介
热门推荐
xmdxcsj的专栏
09-28 1万+
Crf模型 1.   定义 一阶（只考虑y前面的一个）线性条件随机场： 相比于最大熵模型的输入x和输出y，crf模型的输入输出都是序列化以后的矢量，是对最大熵模型的序列扩展。 相比于最大熵模型的另外一个不同是，crf多出了一个维度j（j表示序列x的位置），即任意一个输出yi，都跟所有的输入x有关。 经过变换，crf概率模型可以转化为
一文理解BILSTM神经网络
m0_69378371的博客
05-20 1887
双向长短期记忆网络（BiLSTM，Bidirectional Long Short-Term Memory）**是一种特殊的循环神经网络（RNN），它在自然语言处理（NLP）、时间序列分析等领域具有广泛应用。BiLSTM通过在两个方向上处理输入序列，能够更好地捕捉序列中每个时间步长的上下文信息。
基于BERT嵌入BiLSTM_CRF模型的中文专业术语抽取研究_吴俊1
08-03
标题中的“基于BERT嵌入BiLSTM_CRF模型的中文专业术语抽取研究”是指利用预训练的BERT模型和结合双向长短期记忆网络(BiLSTM)以及条件随机场(CRF)的方法来实现中文专业术语的自动抽取。这种方法旨在提高识别和抽取...
基于BERT-BiLSTM-CRF模型的中文实体识别
05-06
为解决该问题, 本文提出了一种基于BERT-BiLSTM-CRF模型的研究方法. 首先通过BERT模型预处理生成基于上下文信息的词向量, 其次将训练出来的词向量输入BiLSTM-CRF模型做进一步训练处理. 实验结果表明, 该模型在MSRA...
BiLSTM-CRF-NER-PyTorch：此存储库包含BiLSTM-CRF模型的PyTorch实现，用于命名实体识别任务
02-05
使用BiLSTM-CRF模型的NER任务的PyTorch解决方案。 此存储库包含BiLSTM-CRF模型的PyTorch实现，用于命名实体识别任务。 代码结构 在项目的根目录，您将看到： ├── pyner | └── callback | | └── ...
LSTM+CRF模型项目完整代码
12-20
**LSTM+CRF模型项目完整代码** 在自然语言处理（NLP）领域，LSTM（Long Short-Term Memory）和CRF（Conditional Random Fields）是两种常用的深度学习技术，常用于序列标注任务，如命名实体识别（NER）、词性标注...
【CRF系列】第8篇：CRF与深度学习的融合：BiLSTM-CRF模型
最新发布
熵数实验室
04-17 952
自动特征提取：无需手动设计特征函数，BiLSTM能自动学习有效的特征表示端到端训练：整个模型可以联合优化，不需要分阶段训练全局最优解码：CRF层确保考虑整个序列的标签依赖关系约束建模：可以有效避免输出不合法的标签序列更好的性能：在多数序列标注任务上，BiLSTM-CRF比单独使用BiLSTM或CRF效果更好任务模型F1分数英文NER (CoNLL-2003)BiLSTM88.5%英文NER (CoNLL-2003)BiLSTM-CRF90.9%中文分词 (MSRA)
CRF-NER模型
12-11
NER技术实现命名实体识别，可以识别出文本中的人名地名年份组织机构名
[DL]CRF模型解读
sinat_41506268的博客
09-08 1582
CRF（conditional random field，条件随机场）是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔科夫随机场。 想要理解CRF模型，需要先对概率图相关概念有所了解，并与HMM（Hidden Markov Model，隐马尔科夫模型）一起比较学习。（本文只解读思想、原理，不涉及求解过程）
CRF模型在NLP中的运用*
夜阑卧听风吹雨，铁马是你，冰河也是你。
01-21 370
CRF模型在NLP中的运用
自然语言处理
roki
07-10 413
CRF简介 C onditio nal  R andom   F ield ：条件随机场，一种机器学习技术（模型） CRF 由 John Lafferty 最早用于 NLP 技术领域，其在 NLP 技术领域中主要用于文本标注，并有多种应用场景，例如： 分词（标注字的词位信息，由字构词） 词性标注（标注分词的词性，例如：名...
CRF模型——条件随机场模型
MyHeartWillGoOn
12-08 2716
文章目录CRF含义作用隐含假设使用过程维特比算法与HMM的差异 CRF 含义 CRF(Conditional Random Fields), 中文称作条件随机场, 同HMM一样, 它一般也以文本序列数据为输入, 以该序列对应的隐含序列为输出. 作用 同HMM一样, 在NLP领域, CRF用来解决文本序列标注问题. 如分词, 词性标注, 命名实体识别. 隐含假设 隐含序列中每个单元的可能性只与上一个单元有关 使用过程 首先, CRF模型表示为: lambda = CRF(w1, w2, …, w
CRF模型——打通crf模型的任督二脉（一）
zlb872551601的博客
07-24 1646
CRF模型 是nlp领域的经典模型，也是公认的不好学习的模型（相比其他机器学习模型） ，我记得作为小蓝书《统计机器学习》的最后一章，当年看得那叫一个晦涩难懂呢2333333，反正看了一两遍是看不太懂， 网上博客中 照抄小蓝书《统计机器学习》的最后一章的尤为多，也不能说不对，只是对我这种 小白，还是希望能有掰开算法细节和公式细节，甚至源代码细节来看的文章。 网上关于CRF模型的各种文章，我觉得问题在...
Bert-bilstm-crf模型图
02-28
### Bert-BiLSTM-CRF 模型架构概述 Bert-BiLSTM-CRF 是一种结合了预训练语言模型 BERT 和序列标注的经典结构 BiLSTM 及条件随机场 CRF 的混合模型。这种组合能够有效提升命名实体识别 (NER) 或其他序列标注任务的效果。 #### 架构组成 1. **BERT 层** 输入文本通过 BERT 编码器获取上下文表示向量，这些向量包含了丰富的语义信息[^1]。 2. **BiLSTM 层** 接收来自 BERT 输出的特征向量作为输入，并利用双向 LSTM 结构捕捉前后依赖关系，进一步增强局部特征表达能力[^2]。 3. **CRF 层** 位于顶层用于优化标签预测路径的概率分布，确保整个句子级别的最优解而不是简单地逐词分类。 #### 示意性架构图描述 虽然无法直接提供图片形式的架构图，以下是基于文字说明构建的一个简化版 Bert-BiLSTM-CRF 模型架构的文字示意： ``` +-------------------+ | Input Layer | +--------+----------+ | +--------v----------+ | BERT Layer | <- 预训练好的BERT模型负责提取深度语义特征 +--------+----------+ | +--------v----------+ | BiLSTM Layer | <- 处理时间序列数据，加强字符间关联性的建模 +--------+----------+ | +--------v----------+ | CRF Layer | <- 序列级别上的全局约束，提高标注准确性 +-------------------+ ``` 对于更详细的可视化展示，建议查阅相关论文或技术博客中的图形资料来获得直观的理解。 ```python import torch.nn as nn class BertBiLstmCrf(nn.Module): def __init__(self, bert_model, lstm_hidden_size, num_tags): super(BertBiLstmCrf, self).__init__() # 加载预训练的BERT模型 self.bert = bert_model # 定义BiLSTM层 self.lstm = nn.LSTM(input_size=bert_model.config.hidden_size, hidden_size=lstm_hidden_size, bidirectional=True, batch_first=True) # 定义线性变换映射到标记空间 self.linear = nn.Linear(lstm_hidden_size * 2, num_tags) # 初始化CRF层 from transformers import ConditionalRandomField self.crf = ConditionalRandomField(num_tags=num_tags) def forward(self, input_ids, attention_mask=None, labels=None): outputs = self.bert(input_ids=input_ids, attention_mask=attention_mask)[0] sequence_output, _ = self.lstm(outputs) emissions = self.linear(sequence_output) if labels is not None: loss = -self.crf(emissions, tags=labels, mask=attention_mask.byte(), reduction='mean') return loss else: prediction = self.crf.decode(emissions, mask=attention_mask.byte()) return prediction ```
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值