二叉树的基本介绍与常见面试题总结

树的常用术语与二叉树的概念

二叉树常用术语：

1. 根节点：没有前驱结点
2. 父节点
3. 子节点
4. 叶子结点(没有子节点的节点)
5. 节点的权(节点值)
6. 路径(从root节点找到该节点的路线)
7. 层
8. 子树
9. 树的高度
10. 森林：多棵子树构成森林

如下图所示：

二叉树概念：
树有很多种，每个节点最多只能有两个子节点的一种形式称为二叉树。
二叉树的子节点分为左节点和右节点

满二叉树是一种特殊的完全二叉树

1.二叉树前中后序的递归写法

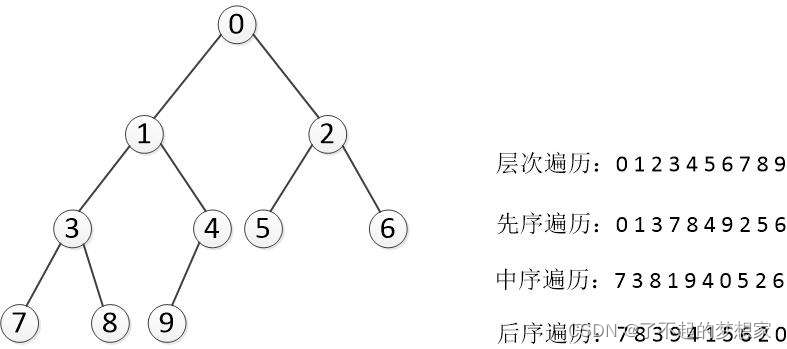
1.1前序遍历

前序遍历：根->左->右

void preOrderTraversal(Node root) {
        if(root == null) {//若为空直接返回
            return;
        }
        System.out.print(root.val+" ");//先打印
        preOrderTraversal(root.left);//向左子树递归
        preOrderTraversal(root.right);//向右子树递归
    }

1.2中序遍历

中序遍历:左->根->右

    void inOrderTraversal(Node root) {
        if(root == null) {
            return;
        }
        inOrderTraversal(root.left);//先向左子树递归
        System.out.print(root.val+" ");//打印
        inOrderTraversal(root.right);//向右子树递归
    }

1.3后序遍历

后序遍历：左->右->根

    void postOrderTraversal(Node root) {
        if(root == null) {
            return;
        }
        postOrderTraversal(root.left);//向左子树递归
        postOrderTraversal(root.right);//向右子树递归
        System.out.print(root.val+" ");//打印
    }

2.二叉树的层序遍历

2.1层序遍历

层序遍历，利用队列先进先出，不为空就入队

    public void levelOrderTraversal(Node root) {
        if(root == null) return;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);//将根节点入队
        while (!queue.isEmpty()) {
            Node top = queue.poll();//弹出一个元素，记录节点
            System.out.print(top.val+" ");//打印该元素
            //每弹出一个元素，就将该元素的左右子树入队
            if(top.left != null) {
                queue.offer(top.left);
            }
            if(top.right!=null) {
                queue.offer(top.right);
            }
        }
    }

在线OJ上的层序遍历：

    //注意返回值是嵌套的，类似于二维数组
    public List<List<Integer>> levelOrder(Node root) {
        List<List<Integer>> ret = new ArrayList<>();
        if(root == null) return ret;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);//A
        while(!queue.isEmpty()) {
            int size = queue.size();//记录每一层数据的个数
            List<Integer> list = new ArrayList<>();//存放每一层的数据
            while(size > 0) {
                Node top = queue.poll();
                //System.out.print(top.val+" ");
                //list.add(top.val);val是char类型，类型不匹配
                if(top.left != null) {
                    queue.offer(top.left);
                }
                if(top.right!=null) {
                    queue.offer(top.right);
                }
                size--;//3->2->1->0
            }
            ret.add(list);
        }
        return ret;
    }

2.2判断一棵二叉树是否为完全二叉树

完全二叉树：每一层从左往右中间没有间隔

采用层序遍历，利用数据结构队列

若是完全二叉树，遍历完到首元素为空的那一层后，队内元素均为null，否则依然有节点，那就不是完全二叉树

    boolean isCompleteTree(Node root) {
        if(root == null) return true;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while(!queue.isEmpty()) {//直到遍历到首元素为空的那一层
            Node top = queue.poll();
            if(top == null) {//遇到null直接退出循环
                break;
            }
            queue.offer(top.left);
            queue.offer(top.right);
        }
        //注意null并不代表没有节点
        while (!queue.isEmpty()) {//查找是否还有节点
            Node top = queue.peek();
            if(top != null) {//若不是全部是null，不是完全二叉树
                return false;
            }
            queue.poll();
        }
        return true;
    }

3.二叉树相关面试题总结

3.1求一棵二叉树的节点个数

1. 遍历思路-求结点个数
   不管哪种遍历方式，遇到节点size++即可

代码示例：

    static int size = 0;
    void getSize1(Node root) {
        if(root == null) {
            return;
        }
        size++;
        getSize1(root.left);
        getSize1(root.right);
    }

2. 子问题思路-求结点个数
   左子树节点数+右子树节点数+1

代码示例：

    int getSize2(Node root) {
        if(root == null) {
            return 0;
        }
        int val = getSize2(root.left)+getSize2(root.right)+1;
        return val;
    }

3.2求一棵二叉树叶子节点个数

1. 遍历思路-求叶子结点个数
   左叶子结点的个数+右叶子节点的个数

叶子结点的特点：root.left == null && root.right == null

代码示例：

    static int leafSize = 0;
    void getLeafSize1(Node root){
        if(root == null) {
            return;
        }
        if(root.left == null && root.right == null) {//叶子结点的特点
            leafSize++;
        }
        getLeafSize1(root.left);
        getLeafSize1(root.right);
    }

2. 子问题思路-求叶子结点个数
   左叶子结点的个数+右叶子节点的个数

代码示例：

    int getLeafSize2(Node root){
        if(root == null) {
            return 0;
        }
        if(root.left == null && root.right == null) {//叶子节点的特点
            return 1;
        }
        int val = getLeafSize2(root.left) + getLeafSize2(root.right);
        return val;
    }

3.3第K层的节点个数

递归一次，K减1一次，直到减到K==1，返回

代码示例：

   int getKLevelSize(Node root, int k) {
        if(root == null) {
            return 0;
        }
        if(k == 1) {
            return 1;
        }
        //只有到第K层才有返回值1，最后返回求和的值
        int val = getKLevelSize(root.left,k-1) + getKLevelSize(root.right,k-1);
        return val;
    }

3.4 获取二叉树的高度

分别求出左右两树的高度取最大值，最后再加1

代码示例：

    int getHeight(Node root) {
        if(root == null) {
            return 0;
        }
        //
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        //每次递归返回时对应的定义值都会+1，最后取最大高度即可
        //return Math.max(leftHeight,rightHeight)+1; √
        return leftHeight > rightHeight ? leftHeight+1:rightHeight+1;//√
        //重复计算过多，×
        //return getHeight(root.left) > getHeight(root.right) ?
        //  getHeight(root.left)+1:getHeight(root.right)+1;
    }

3.5在二叉树中查找值为val的一个节点

遍历整个二叉树，若找到直接返回
并无规定必须采用何种遍历方式，此处采用前序遍历，根左右

代码示例：

    Node find(Node root, char val) {
        if(root == null) {
            return null;
        }
        if(root.val == val) {//找到了直接返回
            return root;
        }
        Node ret = find(root.left,val);//向左递归
        if(ret != null) {
            //找到了！
            return ret;
        }
        ret = find(root.right,val);//向右递归
        //if(ret!=null){
            //找到了
            //return ret;
        //}等价于下面一个return
        return ret;//若找到返回节点，没找到就已经是null

    }

3.6检查两棵树是否相同

若两棵树结构上相同，并且节点上具有相同的值，则认为他们是相同的。

//思路：以子问题的思路解题。遍历这棵树->前中后
//先判断根节点是不是一样的？
//a.一个为空一个不为空或者都不为空但值不一样[结构不同]
//b.都不为空且对应值一样[结构一样]
//此时确定了根，再去确定根的左树和根的右树[和上述一样继续判断]

代码示例：

    public boolean isSameTree(Node p, Node q) {
        //首先判断结构上是否相同
        if(p == null && q != null  || p != null && q == null){
            return false;
        }
        if(p == null && q == null) {
            return true;
        }
        //判断数值是否相同
        if(p.val != q.val) {
            return false;
        }
        //p!=null && q!=null && p.val == q.val
        //此时确定了根，再分别递归左子树和右子树
        return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
    }

3.7判断一棵树是否为另一棵树的子树

如图：B树为A树的子树

//思路：1.root和subRoot是否本身就是两颗相同的树
//2.根的左树root.left和root.subRoot是否相同
//3.根的右树root.right和root.subRoot是否相同
//4.不满足前三个条件，一个为空一个不为空的情况下

代码示例：

    public boolean isSubtree(Node root, Node subRoot) {

        if(root == null) {//防止递归访问时空指针异常
            return false;
        }
        //root和subRoot是否本身就是两颗相同的树
        if(isSameTree(root,subRoot)) {
            return true;
        }
        //根的左树root.left和root.subRoot是否相同
        if(isSubtree(root.left,subRoot)) return true;
        //根的右树root.right和root.subRoot是否相同
        if(isSubtree(root.right,subRoot)) return true;
        //不满足前三个条件，一个为空一个不为空的情况下
        return false;
    }

3.8判断是否为平衡二叉树

解：

//平衡二叉树：每一个节点的左右子树高度差的绝对值不超过1
//先判断根节点是否平衡，再判断根的左右节点是否平衡

代码示例：

    public int maxDepth(Node root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);

        return leftHeight>rightHeight ? leftHeight+1:rightHeight+1;//返回左右子树中的最大深度
    }
    //每个节点都要求高度，N个节点，时间复杂度为O(N^2),由上而下的来求
    public boolean isBalanced1(Node root) {
         //递归到最底部后，空树也是平衡二叉树，此时返回true
        if(root == null) return true;
        //分别取得左子树和右子树的高度
        int leftHeight = maxDepth(root.left);
        int rightHeight = maxDepth(root.right);
        //每一个节点的左右子树高度差的绝对值不超过1，并且左右子树也是平衡的
        return Math.abs(leftHeight-rightHeight) <= 1 &&
                isBalanced1(root.left) && isBalanced1(root.right) ;

    }

O(N)的解法

    public int maxDepth2(Node root) {
        if(root == null) {
            return 0;
        }
        int leftHeight = maxDepth2(root.left);
        int rightHeight = maxDepth2(root.right);
        //预防 leftHeight || leftHeight == -1  另外一个==0
        if( leftHeight >= 0 && rightHeight >= 0 &&
                Math.abs(leftHeight-rightHeight) <= 1 ) {
                //由下而上，一边求深度一边判断(Math.abs()<=1)
            return Math.max(leftHeight,rightHeight) + 1;
        }else{//只要是遇到非平衡，没一层都返回-1
            return -1;
        }
    }
    public boolean isBalanced(Node root) {
        return maxDepth2(root) >= 0;//若存在不平衡则返回值变为-1
    }

3.9给定一个二叉树，判断其是否镜像对称

镜像对称的二叉树，以根节点为轴左子树和右子树结构和数值上对称

//思路：左树的左树和右树的右树，左树的右树和右树的左树。
//左树和右树是不是对称的

代码示例：

    public boolean isSymmetricChild(Node leftTree,
                                    Node rightTree) {
         //一个为空一个不为空
        if(leftTree == null && rightTree != null ||
                leftTree != null && rightTree == null) {
            return false;
        }
        //两个都为空
        if(leftTree == null && rightTree == null) {
            return true;
        }
        if(leftTree.val != rightTree.val) {//值不同
            return false;
        }
        return isSymmetricChild(leftTree.left,rightTree.right)//左树的左树和右树的右树
                && isSymmetricChild(leftTree.right,rightTree.left);//左树的右树和右树的左树。
    }
    public boolean isSymmetric(Node root) {
        if(root == null) return false;
        return isSymmetricChild(root.left,root.right);
    }

3.10寻找最近公共祖先

可能的情况：
1.其中一个可能是最近祖先

2.p和q在根的两侧

p和q均在二叉树内，并且p!=q

方法：

递归：
左右两边均不为空     root
左边为空，右边不为空   √
左边不为空，右边为空   √
左右两边均为空        ×

代码示例：

    public Node lowestCommonAncestor(Node root, Node p, Node q) {
        if(root == null) return null;//空树 是没有公共祖先的
        if(root == p || root == q) {//遇到节点p或q直接返回节点
            return root;
        }
        //向树内部递归，直到递进到p或q，或者到null
        Node leftTree = lowestCommonAncestor(root.left,p,q);
        Node rightTree = lowestCommonAncestor(root.right,p,q);
        //对递进完成后的leftTree和rightTree进行分析，回归
        //左右均不为空，返回节点
        if(leftTree != null && rightTree != null) {
            return root;
        }
        //左右有一个不为空，返回非空的哪一个
        if(leftTree == null && rightTree != null) {
            return rightTree;
        }
        if(leftTree != null && rightTree == null) {
            return leftTree;
        }
        //左右均为空返回空
        if(leftTree == null && rightTree == null) {
            return null;
        }
        return null;
    }

3.11将一个搜索二叉树转变为双向链表（有序）

搜索二叉树：左子树小于根节点，右子树大于根节点

解：
中序遍历时，每遍历一个节点就修改一个节点的指向

方法：采用中序遍历，每遍历一个节点就修改一个节点的指向。left改为前驱，right改为后继

代码示例：

    TreeNode prev = null;
    public void ConvertChild(TreeNode pCur) {
        if(pCur == null) return;
        //改变节点之间的连接，关键的三行代码
        ConvertChild(pCur.left);
        //----------------
        pCur.left = prev;
        if(prev != null) {//第一次连接时节点的prev为空，跳过，防止发生空指针异常
            prev.right = pCur;
        }
        prev = pCur;
        //----------------
        ConvertChild(pCur.right);
    }


    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree == null) return null;

        ConvertChild(pRootOfTree);//改变结构

        TreeNode head = pRootOfTree;//此时指向的是双向链表的尾

        while(head.left != null) {//找到双向链表头节点
            head = head.left;
        }
        return head;//返回头节点

    }

3.12利用前序遍历和中序遍历来构建二叉树

前序遍历：根 左 右 -》用来确定根，从前往后
中序遍历：左 根 右 -》左边是左子树，右边是右子树

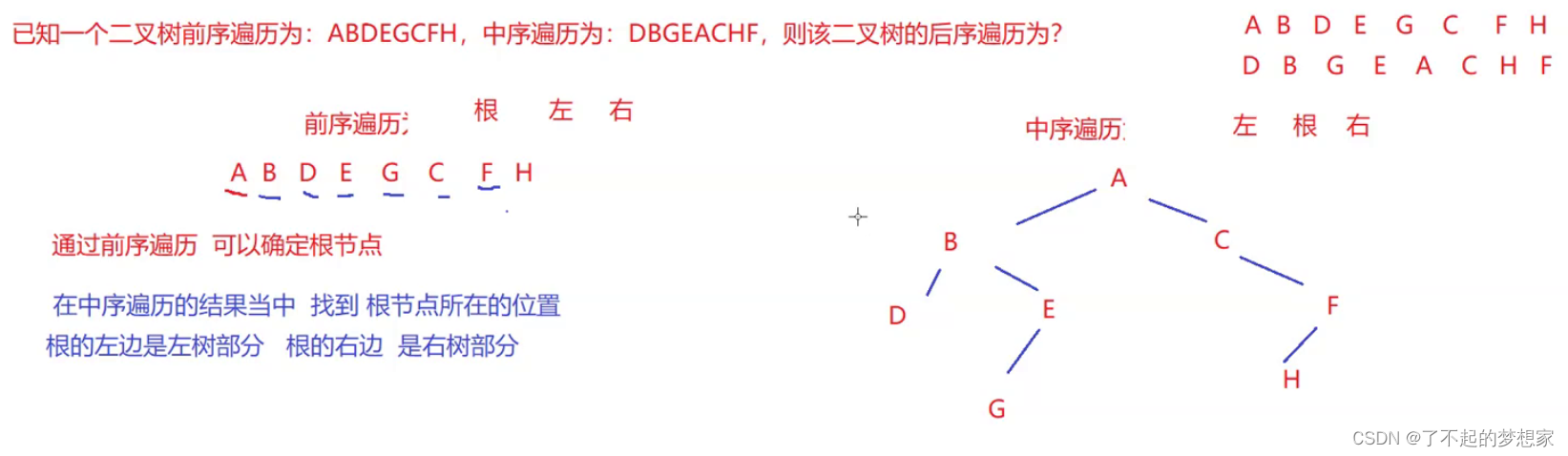
//方法：采用前序遍历的方式

代码示例：

    public int preIndex = 0;//保证每次递归时不会被重新赋值为0
    public TreeNode buildTreeChild(int[] preorder ,int[] inorder,int inbegin,int inend) {
        if(inbegin > inend) {//递归的终止条件
            return null; //此时节点 没有 左树 或者 没有右树
        }
        TreeNode root = new TreeNode(preorder[preIndex]);
        //找到在中序遍历中的位置
        int rootIndex = findInorderIndex(inorder,inbegin,inend,preorder[preIndex]);
        preIndex++;//前序遍历 根左右，根的值往后移一位
        //建左右子树，注意左子树与右子树遍历时参数不同
        root.left = buildTreeChild(preorder ,inorder,inbegin,rootIndex-1);
        root.right = buildTreeChild(preorder ,inorder,rootIndex+1,inend);
        //建树完毕，返回
        return root;
    }

    public int findInorderIndex(int[] inorder,int inbegin,int inend,int key) {
        for(int i = inbegin;i <= inend;i++) {//找到在中序遍历中的位置
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if(preorder == null || inorder == null) return null;
        return buildTreeChild(preorder, inorder,0,inorder.length-1);
    }

3.13利用后序遍历和中序遍历来构建二叉树

与上题一样
后序遍历：左右根 -》确定根，从后往前遍历
中序遍历：左根右 -》确定左右子树的位置

方法：采用后序遍历的方式

代码示例：

    public int postIndex = 0;
    public TreeNode buildTreeChild(int[] postorder ,int[] inorder,int inbegin,int inend) {
        if(inbegin > inend) {
            return null; //此时节点 没有 左树 或者 没有右树
        }
        TreeNode root = new TreeNode(postorder[postIndex]);
        //找到在中序遍历中的位置
        int rootIndex = findInorderIndex(inorder,inbegin,inend,postorder[postIndex]);
        postIndex--;//后序遍历，左右根，根的值从后往前移一位
        //建左右子树，注意左子树与右子树遍历时参数不同
        root.right = buildTreeChild(postorder ,inorder,rootIndex+1,inend);
        root.left = buildTreeChild(postorder ,inorder,inbegin,rootIndex-1);
        return root;
    }

    public int findInorderIndex(int[] inorder,int inbegin,int inend,int key) {
        for(int i = inbegin;i <= inend;i++) {
            if(inorder[i] == key) {
                return i;
            }
        }
        return -1;
    }

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        if(postorder == null || inorder == null) return null;
        postIndex = postorder.length-1;
        return buildTreeChild(postorder, inorder,0,inorder.length-1);
    }

3.14二叉树转字符串

示例1

左树和右树都为空 ++++ 以及 ++++ 左不为空右树为空省略()

示例2

左树为空，右不为空不可省略，加()

方法：前序遍历这棵树，合适的时机加上()即可

代码示例：

    public void tree2strChild(TreeNode t,StringBuilder sb) {
        if(t == null) return;
        sb.append(t.val);

        if(t.left == null) {
            if(t.right == null) {
                return;
            }else{//左为空，右不为空，+()
                sb.append("()");
            }
        }else{//左不为空，加元素（sb.val）
            sb.append("(");
            tree2strChild(t.left,sb);
            sb.append(")");
        }
        //以上是t的左树情况全部解决完成
        if(t.right == null) {//左不为空，右为空，直接省略
            return;
        }else{//不为空，+元素
            sb.append("(");
            tree2strChild(t.right,sb);
            sb.append(")");
        }
    }

    public String tree2str(TreeNode root) {
        if(root == null) return null;
        StringBuilder sb  = new StringBuilder();
        tree2strChild(root,sb);
        return sb.toString();
    }

4.二叉树前中后序的非递归写法

非递归：模拟栈的实现方式

4.1非递归实现前序遍历

前序遍历：根左右

    void preOrderTraversalNor(Node root) {
        if(root == null) return;
        Stack<Node> stack = new Stack<>();//模拟栈的实现方式，先入后出
        Node cur = root;
        while (cur != null || !stack.empty()) {//栈不为空就可以一直回归
            while (cur != null) {//入栈+递归直到为空
                stack.push(cur);//入栈，在回归的时候可以找到右子树
                System.out.print(cur.val + " ");
                cur = cur.left;
            }
            Node top = stack.pop();//遇到空，弹出栈顶元素，删除。开始向右子树递归
            cur = top.right;//1、null，栈不为空   2、不是null 的情况，直接进入循环
        }
        System.out.println();
    }

4.2非递归中序遍历

中序遍历：左根右

    void inOrderTraversalNor(Node root) {
        if(root == null) return;
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        while (cur != null || !stack.empty()) {
            while (cur != null) {//先遍历到最左边
                stack.push(cur);
                cur = cur.left;
            }
            Node top = stack.pop();//弹出栈顶元素，删除
            System.out.print(top.val + " ");
            cur = top.right;
        }
        System.out.println();
    }

4.3非递归后序遍历

后序遍历：左右根

    void postOrderTraversalNor(Node root){
        if(root == null) return;
        Node prev = null;//指向刚打印的节点
        Stack<Node> stack = new Stack<>();
        Node cur = root;
        while (cur != null || !stack.empty()) {//cur不为空和栈不为空都可以进入循环
            while (cur != null) {
                stack.push(cur);
                cur = cur.left;
            }
            cur = stack.peek();//获取栈顶元素，不删除
            if (cur.right == null || cur.right == prev) {//右子树为空或者节点刚被打印
                stack.pop();//弹出栈顶元素，删除
                System.out.print(cur.val + " ");
                prev = cur;
                cur = null;// 这个y被打印了  不能再次入栈
            } else {
                cur = cur.right;
            }
        }
    }