[Python]代码随想录Day34[动态规划]

动规五部曲：

1.dp数组的定义以及下标的含义 dp[i][j]   dp[i] 

2.递推公式（是动态规划的一部分）

3.dp数组如何初始化

4.遍历顺序 01背包  遍历背包 后遍历物品  or  先遍历物品再遍历背包    排列组合的for循环

5.打印dp数组

62.不同路径

定义二维dp数组dp[i][j]

1.dp数组的定义以及下标的含义 dp[i][j]   

从（0,0）到（i,j）有多少种不同的路径

2.递推公式（是动态规划的一部分）

dp[i - 1][j]   dp[i][j - 1]

dp[i,j]=dp[i - 1][j] + dp[i][j - 1]

3.dp数组如何初始化

dp[0][j]

dp[i][0]

for (i=0; i<m; i +1)  dp[i][0] = 1 

for(j=0;  j<n; j+1) dp[0][j] =1

4.遍历顺序 

从左往右 从上往下

5.打印dp数组

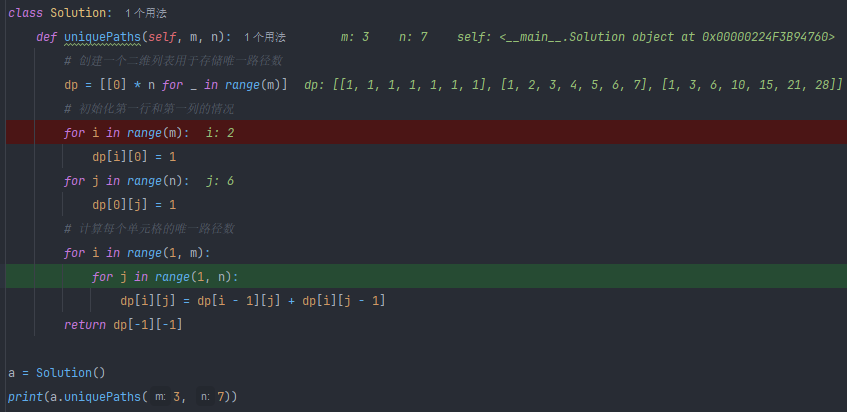
基础动态规划版本

class Solution:
    def uniquePaths(self, m, n):
        # 创建一个二维列表用于存储唯一路径数
        dp = [[0] * n for _ in range(m)]
        # 初始化第一行和第一列的情况
        for i in range(m):
            dp[i][0] = 1
        for j in range(n):
            dp[0][j] = 1
        # 计算每个单元格的唯一路径数
        for i in range(1, m):
            for j in range(1, n):
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[-1][-1]

递归

class Solution:
    def uniquePaths(self, m, n):
        if m == 1 or n == 1:
            return 1
        return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)

63. 不同路径 II

 定义二维dp数组dp[i][j]

1.dp数组的定义以及下标的含义 dp[i][j]   

从（0,0）到（i,j）有多少种不同的路径

2.递推公式（是动态规划的一部分）判断是否遇到障碍

dp[i - 1][j]   dp[i][j - 1]

dp[i,j]=dp[i - 1][j] + dp[i][j - 1]

3.dp数组如何初始化！！！

初始化有很大的不同  起始位置就有障碍的话 就没法走了

for（int i = 0;i <m;and obs[i][0] ==0;i ++）dp[i][0] = 1

for(int j = 0,j <n:and obs[0][j] ==0; j++)  dp[0][j] =1

4.遍历顺序 

从左往右 从上往下

5.打印dp数组

dp[-1][-1]

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        m = len(obstacleGrid)
        n = len(obstacleGrid[0])
        # 如果起始点终点有障碍物,直接返回0
        if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
            return 0
        dp = [[0] * n for _ in range(m)]
        # 设置起始路径数为1 
        dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0
        # 计算第一列的路径数
        for i in range(1,m):
            if obstacleGrid[i][0] == 0:
                dp[i][0] = dp[i - 1][0]

        # 计算第一行的路径数
        for j in range(1, n):
            if obstacleGrid[0][j] == 0:
                dp[0][j] = dp[0][j - 1]
    
        # 设置其他路径数
        for i in range(1,m):
            for j in range(1,n):
                if obstacleGrid[i][j] == 1:
                    continue
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        return dp[-1][-1]

343.整数拆分 （可跳过）

尽量拆成相同的数 10 = 3 3 4 

1.dp数组的定义以及下标的含义 dp[i][j]   

dp[i]  对i进行拆分，得到最大的乘积为dp[i]

2.递推公式（是动态规划的一部分）判断是否遇到障碍

i  j * (1 - j)

j * dp[i - j]  3个数及以上

其实就是固定j之后，拆分i-j就已经把所有的情况，包括拆分j的情况都给包含了

1 * 5 

2 * 4

3 * 2

4 * 2

5 * 1 

3.dp数组如何初始化！！！

4.遍历顺序 

5.打印dp数组

class Solution:
         # 假设对正整数 i 拆分出的第一个正整数是 j（1 <= j < i），则有以下两种方案：
        # 1) 将 i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j * (i-j)
        # 2) 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j * dp[i-j]
    def integerBreak(self, n):
        dp = [0] * (n + 1)   # 创建一个大小为n+1的数组来存储计算结果
        dp[2] = 1  # 初始化dp[2]为1，因为当n=2时，只有一个切割方式1+1=2，乘积为1
       
        # 从3开始计算，直到n
        for i in range(3, n + 1):
            # 遍历所有可能的切割点
            for j in range(1, i // 2 + 1):

                # 计算切割点j和剩余部分(i-j)的乘积，并与之前的结果进行比较取较大值
                
                dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)
        
        return dp[n]  # 返回最终的计算结果