LeetCode 1895. 最大的幻方

1895. 最大的幻方

一个 k x k 的 幻方 指的是一个 k x k 填满整数的方格阵，且每一行、每一列以及两条对角线的和 全部相等 。幻方中的整数 不需要互不相同 。显然，每个 1 x 1 的方格都是一个幻方。

给你一个 m x n 的整数矩阵 grid ，请你返回矩阵中 最大幻方 的 尺寸 （即边长 k）。

示例 1：

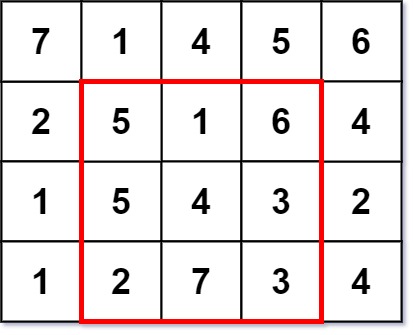
输入：grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出：3
解释：最大幻方尺寸为 3 。
每一行，每一列以及两条对角线的和都等于 12 。
- 每一行的和：5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和：5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和：5+4+3 = 6+4+2 = 12

示例 2：

输入：grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出：2

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 50
• 1 <= grid[i][j] <= 10^6

---

提示 1

Check all squares in the matrix and find the largest one.

 

解法：枚举正方形 + 前缀和

思路与算法

我们只需要按照从大到小的顺序枚举正方形的边长 edge，再枚举给定的矩阵 grid 中所有边长为 edge 的正方形，并依次判断它们是否满足幻方的要求即可。

这样做的时间复杂度是多少呢？我们记 x=min(m,n)，那么 edge 的范围为 [1,x]，边长为 edge 的正方形有 (m−edge+1)(n−edge+1)=O(mn) 个，对于每个正方形，我们需要计算其每一行、列和对角线的和，一共有 edge 行 edge 列以及 2 条对角线，那么计算这些和的总时间复杂度为 ((2⋅edge+2)⋅edge)=O(x^2)。将所有项相乘，总时间复杂度即为 O(x^3*m*n)。

我们无法 100% 保证 O(x^3*mn) 的算法可以在规定时间内通过所有的测试数据：虽然它的时间复杂度看起来很大，但是常数实际上很小，如果代码写得比较优秀，还是有通过的机会的。

但做一些不复杂的优化也是很有必要的。一个可行的优化点是：我们可以预处理出矩阵 grid 每一行以及每一列的前缀和，这样对于计算和的部分：

每一行只需要 O(1) 的时间即可求和，所有的 edge 行的总时间复杂度为 O(x)；

每一列只需要 O(1) 的时间即可求和，所有的 edge 列的总时间复杂度为 O(x)；

我们没有预处理对角线的前缀和，这是因为对角线只有 2 条，即使我们直接计算求和，时间复杂度也为 O(2⋅x)=O(x)。

因此，求和部分的总时间复杂度从 O(x^2) 降低为 O(x)，总时间复杂度降低为 O(x^2 * mn)，对于本题 m,n≤50 的范围，该时间复杂度是合理的。

前缀和的具体实现过程可以参考下面的代码。

优化

我们只需要在 [2,x] 的范围内从大到小遍历 edge 即可，这是因为边长为 1 的正方形一定是一个幻方。

Java版：

class Solution {
    public int largestMagicSquare(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] rowsum = new int[m][n];
        int[][] colsum = new int[m][n];
        
        // 每一行的前缀和
        for (int i = 0; i < m; i++) {
            rowsum[i][0] = grid[i][0];
            for (int j = 1; j < n; j++) {
                rowsum[i][j] = rowsum[i][j - 1] + grid[i][j];
            }
        }

        // 每一列的前缀和
        for (int j = 0; j < n; j++) {
            colsum[0][j] = grid[0][j];
            for (int i = 1; i < m; i++) {
                colsum[i][j] = colsum[i - 1][j] + grid[i][j];
            }
        }

        // 从大到小枚举边长 edge
        for (int edge = Math.min(m, n); edge >= 2; edge--) {
            // 枚举正方形的左上角位置 (i,j)
            for (int i = 0; i <= m - edge; i++) {
                for (int j = 0; j <= n - edge; j++) {
                    // 先计算第一行的和作为样本
                    int target = rowsum[i][j + edge - 1] - (j > 0 ? rowsum[i][j - 1] : 0);
                    boolean check = true;

                    // 枚举每一行并用前缀和直接求和
                    // 由于我们已经拿第一行作为样本了，这里可以跳过第一行
                    for (int ii = i + 1; ii < i + edge; ii++) {
                        if (rowsum[ii][j + edge - 1] - (j > 0 ? rowsum[ii][j - 1] : 0) != target) {
                            check = false;
                            break;
                        }
                    }
                    if (!check) {
                        continue;
                    }

                    // 枚举每一列并用前缀和直接求和
                    for (int jj = j; jj < j + edge; jj++) {
                        if (colsum[i + edge - 1][jj] - (i > 0 ? colsum[i - 1][jj] : 0) != target) {
                            check = false;
                            break;
                        }
                    }
                    if (!check) {
                        continue;
                    }

                    // d1 和 d2 分别表示两条对角线的和
                    int d1 = 0, d2 = 0;
                    // 两条对角线直接遍历求和
                    for (int k = 0; k < edge; k++) {
                        d1 += grid[i + k][j + k];
                        d2 += grid[i + k][j + edge -1 - k];
                    }
                    if (d1 == target && d2 == target) {
                        return edge;
                    }
                }
            }
        }
        return 1;
    }
}

Python3版：

class Solution:
    def largestMagicSquare(self, grid: List[List[int]]) -> int:
        m = len(grid)
        n = len(grid[0])
        rowsum = [[0] * n for _ in range(m)]
        colsum = [[0] * n for _ in range(m)]

        # 每一行的前缀和
        for i in range(m):
            rowsum[i][0] = grid[i][0]
            for j in range(1, n):
                rowsum[i][j] = rowsum[i][j - 1] + grid[i][j]

        # 每一列的前缀和
        for j in range(n):
            colsum[0][j] = grid[0][j]
            for i in range(1, m):
                colsum[i][j] = colsum[i - 1][j] + grid[i][j]
        
        # 从大到小枚举边长 edge
        for edge in range(min(m, n), 1, -1):
            # 枚举正方形的左上角位置 (i,j)
            for i in range(m - edge + 1):
                for j in range(n - edge + 1):
                    # 先计算第一行的和作为样本
                    target = rowsum[i][j + edge - 1] - (rowsum[i][j - 1] if j > 0 else 0)
                    check = True

                    # 枚举每一行并用前缀和直接求和
                    for ii in range(i + 1, i + edge):
                        if rowsum[ii][j + edge - 1] - (rowsum[ii][j - 1] if j > 0 else 0) != target:
                            check = False
                            break
                    if not check:
                        continue
                    
                    # 枚举每一列并用前缀和直接求和
                    for jj in range(j, j + edge):
                        if colsum[i + edge - 1][jj] - (colsum[i - 1][jj] if i > 0 else 0) != target:
                            check = False 
                            break
                    if not check:
                        continue 
                    
                    # d1 和 d2 分别表示两条对角线的和
                    d1, d2 = 0, 0
                    # 两条对角线直接遍历求和
                    for k in range(edge):
                        d1 += grid[i + k][j + k]
                        d2 += grid[i + k][j + edge - 1 - k]
                    if d1 == target and d2 == target:
                        return edge 
        return 1 
                    
                    

复杂度分析

• 时间复杂度：O(mn * min(m,n)^2)。

• 空间复杂度：O(mn)，即为存储前缀和需要的空间。