二叉树的最近公共祖先（两种思路）

原创已于 2022-03-01 16:11:23 修改 · 320 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#java #leetcode #数据结构

于 2022-02-28 21:46:43 首次发布

这篇博客介绍了两种方法在二叉搜索树中寻找两个指定结点的最近公共祖先。思路一利用递归，当找到一个结点时返回其父结点，直到找到公共祖先。思路二转化问题为链表求交点，通过记录路径并在路径中找到公共结点。这两种方法均能有效解决该问题。

题目：

思路一：

思路二：

题目：

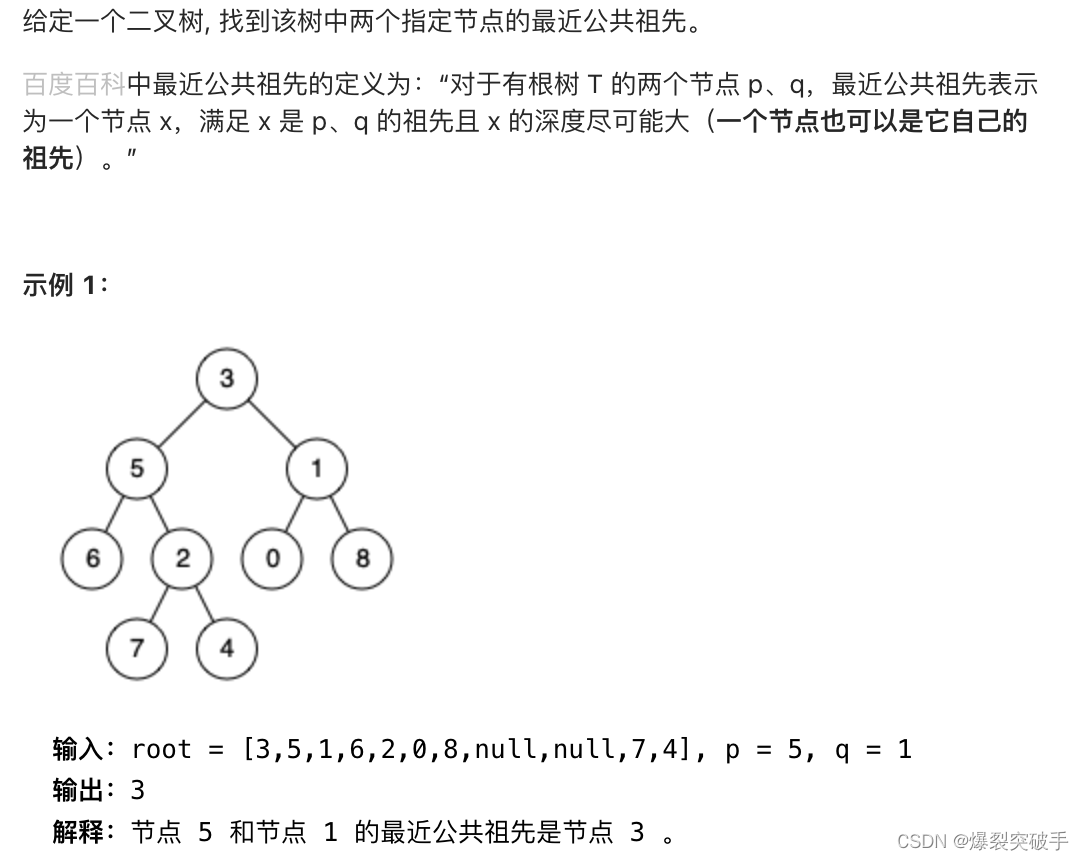
思路一：

分析：

直接通过递归在左右子树寻找目标结点。

1.通过分析二叉树搜索树可以得知：p，q两个结点在二叉树上存在的情况如下有分别存在与不同子树，存在与同一棵子树。

2.设置递归终止条件：当前root为空时结束当前进行的方法。遇到p == root 或者q == root 则直接返回当前root。

3.通过子问题思路，分别递归搜索左右子树。

代码：

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) return null;
        if (p == root || q == root) return root;
        TreeNode Left = lowestCommonAncestor(root.left,p,q);
        TreeNode Right = lowestCommonAncestor(root.right,p,q);
        if (Left != null && Right != null) return root;
        if (Left != null && Right == null) return Left;
        if (Left == null && Right != null) return Right;
        return null;
    }

思路二：

分析：

把问题转化为链表求交点的思路。

1.首先排除root为空或者node为空的情况，先将root放入栈中。

2.设置递归结束条件：root与node相等返回true。

3.递归分别在左右子树目标结点，在哪边找到返回true，这时在路径记录在栈中；若左右子树都找不到，则将其从栈中退出。

4.创建两个栈，分别存放寻找p和q的路径。比较两个栈的大小，较大的栈先出差值个元素后，在同步出栈，直到找到相同的结点。

代码：

//root代表根结点。node代表查找的目标结点。stack代表存放查找路径的栈。
public boolean getPath (TreeNode root,TreeNode node,Stack<TreeNode> stack) {
        if (root == null || node == null) return false;
        stack.push(root);
        if (root == node) return true;
        boolean flg = getPath(root.left,node,stack);
        if (flg) {
            return true;
        }
        flg = getPath(root.right,node,stack);
        if (flg) {
            return true;
        }
        //注意当前该结点root的左右子树没找到node应该将当前root退出栈
        stack.pop();
        return false;
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();

        getPath(root,p,stack1);
        getPath(root,q,stack2);

        int num1 = stack1.size();
        int num2 = stack2.size();
        int num = Math.abs(num1 - num2);
        
        if (num1 > num2) {
            while (num != 0) {
                stack1.pop();
                num--;
            }
            while (!stack1.isEmpty() && !stack2.isEmpty()) {
                if (stack1.peek() == stack2.peek()) {
                    return stack1.peek();
                }
                stack1.pop();
                stack2.pop();
            }
            return null;
        } else {
            while (num != 0) {
                stack2.pop();
                num--;
            }
            while (!stack1.isEmpty() && !stack2.isEmpty()) {
                if (stack1.peek() == stack2.peek()) {
                    return stack1.peek();
                }
                stack1.pop();
                stack2.pop();
            }
            return null;
        }
    }