本文深入探讨了进制位算法，包括二进制、八进制、十进制和十六进制之间的转换原理和方法。介绍了从低位到高位的计算规则，如二进制的逢2进1，八进制的逢8进1，十六进制的逢16进1。详细阐述了如何通过取余、除法和位权相加的方法进行进制转换，并通过多个案例展示了如何将这些理论应用于实际问题，如八进制转十进制、十进制转二进制等。
目录
进制的由来
-- 对于整数，有四重表现形式：
*** 二进制：0和1，满2进1.
*** 八进制：0-7，满8进1，用0开头表示。《八进制数，其实就是二进制位的 3个二进制位 为一个八进制位》111=7
例：
010-101-110
2 5 6 =八进制数：0256
*** 十进制：0-9，满10进1。
*** 十六进制：0-9，A-F，满16进1，用0x开头表示。《十六进制，其实就是二进制中的四个二进制位为一个十六进制位》1111=15
例：
1010-1110
10 14 =十六进制数：0xAE
byte 个字节=8个二进制位 = 8个bit
1k =1024 个字节
-- 负数二进制的转换：
*** 其实就是这个数，的正数的二进制取反，加1.
例：-6
6的二进制 0000-0110
取反 1111-1001
加1 +0000-0001
=1111-1010
-6
负数的二进制的最高位是1.
-- 在程序中找到一个数的十六进制的表示：
《要用num十六进制的表示法与1111比较《就是15》， 4个二进制位进行比较 ,num再右移4位进行比较《就是num>>>4》》
1.2.3.4.5.6.7.8.9.A .B .C .D .E .F
1.2.3.4.5.6.7.8.9.10.11.12.13.14.15
进制 机制 计算位 最大值二进制 单元 表示法
2进制 逢2进1 1 1 0，1 0b ****
4进制 逢4进1 2 11 0，1，2，3
8进制 逢8进1 3 111 0，1，2，3，4，5，6，7 0****
10进制 逢10进1 0，1，2，3，4，5，6，7，8，9
16进制 逢16进1 4 1111 0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F 0x****
32进制 逢32进1 5 11111 0,1 ~ 9,A,B ~ V(除了W,X,Y,Z)
1.1.3算法主要框架
在数字后面加上不同的字母来表示不同的进位制。B（Binary)表示二进制，O（Octal）表示八进制，D（Decimal）或不加表示十进制，H（Hexadecimal）表示十六进制。例如：(101011)B=(53)O=(43)D=(2B)H
(一) （二、八、十六进制） → （十进制）
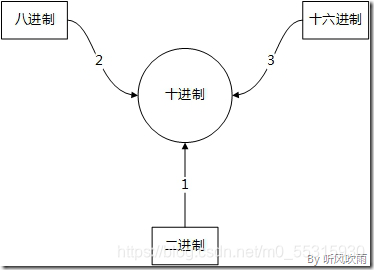
（Figure2：其他进制转换为十进制）
方法：二进制数从低位到高位（即从右往左）计算，第0位的权值是2的0次方，第1位的权值是2的1次方，第2位的权值是2的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
例：将二进制的(101011)B转换为十进制的步骤如下：
1. 第0位 1 x 2^0 = 1；
2. 第1位 1 x 2^1 = 2；
3. 第2位 0 x 2^2 = 0；
4. 第3位 1 x 2^3 = 8；
5. 第4位 0 x 2^4 = 0；
6. 第5位 1 x 2^5 = 32；
7. 读数，把结果值相加，1+2+0+8+0+32=43，即(101011)B=(43)D。
方法：八进制数从低位到高位（即从右往左）计算，第0位的权值是8的0次方，第1位的权值是8的1次方，第2位的权值是8的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
八进制就是逢8进1，八进制数采用 0～7这八数来表达一个数。
例：将八进制的(53)O转换为十进制的步骤如下：
1. 第0位 3 x 8^0 = 3；
2. 第1位 5 x 8^1 = 40；
3. 读数，把结果值相加，3+40=43，即(53)O=(43)D。
方法：十六进制数从低位到高位（即从右往左）计算，第0位的权值是16的0次方，第1位的权值是16的1次方，第2位的权值是16的2次方，依次递增下去，把最后的结果相加的值就是十进制的值了。
十六进制就是逢16进1，十六进制的16个数为0123456789ABCDEF。
例：将十六进制的(2B)H转换为十进制的步骤如下：
1. 第0位 B x 16^0 = 11；
2. 第1位 2 x 16^1 = 32；
3. 读数，把结果值相加，11+32=43，即(2B)H=(43)D。
(二) （十进制） → （二、八、十六进制）
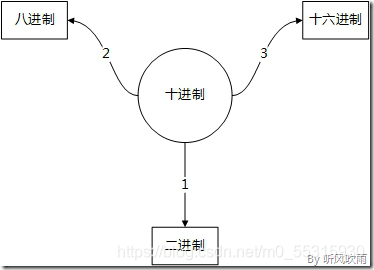
（Figure3：十进制转换为其它进制）
方法：除2取余法，即每次将整数部分除以2，余数为该位权上的数，而商继续除以2，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数读起，一直到最前面的一个余数。
例：将十进制的(43)D转换为二进制的步骤如下：
1. 将商43除以2，商21余数为1；
2. 将商21除以2，商10余数为1；
3. 将商10除以2，商5余数为0；
4. 将商5除以2，商2余数为1；
5. 将商2除以2，商1余数为0；
6. 将商1除以2，商0余数为1；
7. 读数，因为最后一位是经过多次除以2才得到的，因此它是最高位，读数字从最后的余数向前读，101011，即(43)D=(101011)B。
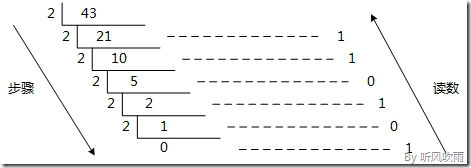
（Figure4：图解十进制 → 二进制）
方法1：除8取余法，即每次将整数部分除以8，余数为该位权上的数，而商继续除以8，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数。
例：将十进制的(796)D转换为八进制的步骤如下：
1. 将商796除以8，商99余数为4；
2. 将商99除以8，商12余数为3；
3. 将商12除以8，商1余数为4；
4. 将商1除以8，商0余数为1；
5. 读数，因为最后一位是经过多次除以8才得到的，因此它是最高位，读数字从最后的余数向前读，1434，即(796)D=(1434)O。
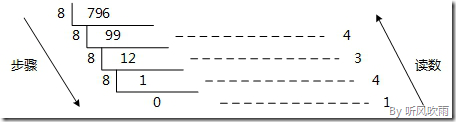
（Figure5：图解十进制 → 八进制）
方法2：使用间接法，先将十进制转换成二进制，然后将二进制又转换成八进制；
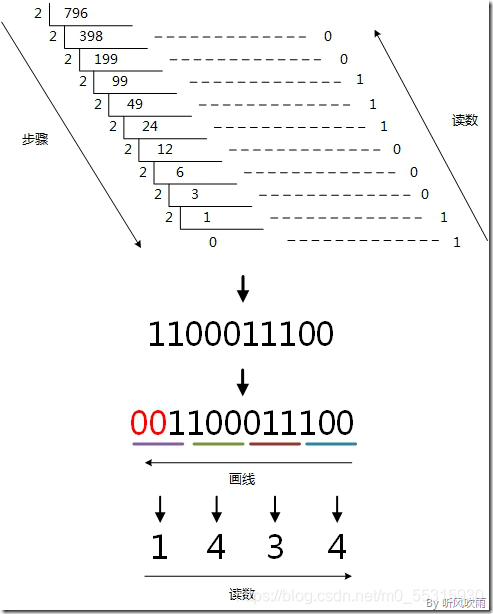
（Figure6：图解十进制 → 八进制）
方法1：除16取余法，即每次将整数部分除以16，余数为该位权上的数，而商继续除以16，余数又为上一个位权上的数，这个步骤一直持续下去，直到商为0为止，最后读数时候，从最后一个余数起，一直到最前面的一个余数。
例：将十进制的(796)D转换为十六进制的步骤如下：
1. 将商796除以16，商49余数为12，对应十六进制的C；
2. 将商49除以16，商3余数为1；
3. 将商3除以16，商0余数为3；
4. 读数，因为最后一位是经过多次除以16才得到的，因此它是最高位，读数字从最后的余数向前读，31C，即(796)D=(31C)H。
（Figure7：图解十进制 → 十六进制）
方法2：使用间接法，先将十进制转换成二进制，然后将二进制又转换成十六进制；
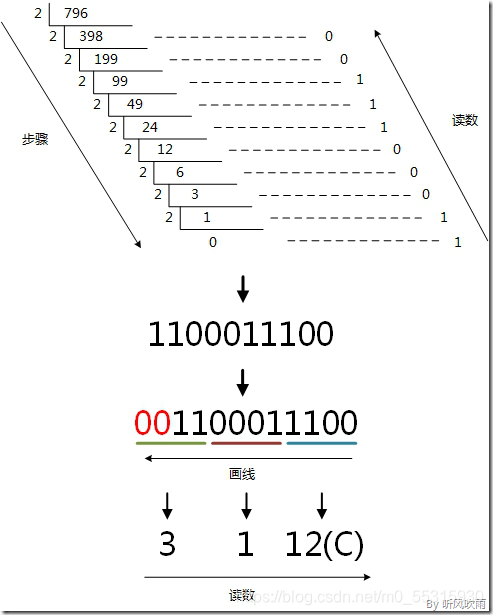
（Figure8：图解十进制 → 十六进制）
(三) （二进制） ↔ （八、十六进制）
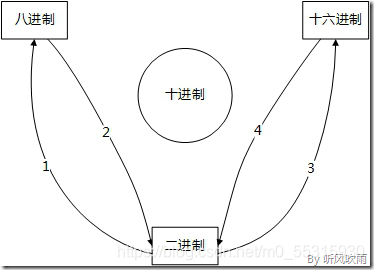
（Figure9：二进制转换为其它进制）
方法：取三合一法，即从二进制的小数点为分界点，向左（向右）每三位取成一位，接着将这三位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的八进制数。如果向左（向右）取三位后，取到最高（最低）位时候，如果无法凑足三位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足三位。
例：将二进制的(11010111.0100111)B转换为八进制的步骤如下：
1. 小数点前111 = 7；
2. 010 = 2；
3. 11补全为011，011 = 3；
4. 小数点后010 = 2；
5. 011 = 3；
6. 1补全为100，100 = 4；
7. 读数，读数从高位到低位，即(11010111.0100111)B=(327.234)O。
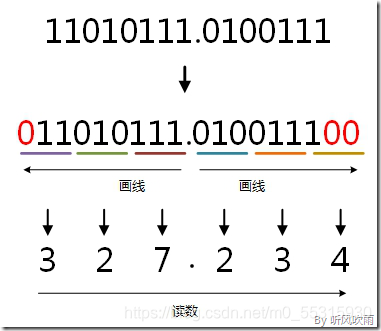
（Figure10：图解二进制 → 八进制）
二进制与八进制编码对应表：
| 二进制 | 八进制 |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
- 八进制 → 二进制
方法：取一分三法，即将一位八进制数分解成三位二进制数，用三位二进制按权相加去凑这位八进制数，小数点位置照旧。
例：将八进制的(327)O转换为二进制的步骤如下：
1. 3 = 011；
2. 2 = 010；
3. 7 = 111；
4. 读数，读数从高位到低位，011010111，即(327)O=(11010111)B。
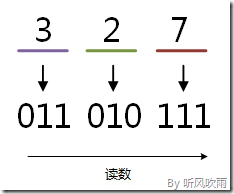
（Figure11：图解八进制 → 二进制）
方法：取四合一法，即从二进制的小数点为分界点，向左（向右）每四位取成一位，接着将这四位二进制按权相加，然后，按顺序进行排列，小数点的位置不变，得到的数字就是我们所求的十六进制数。如果向左（向右）取四位后，取到最高（最低）位时候，如果无法凑足四位，可以在小数点最左边（最右边），即整数的最高位（最低位）添0，凑足四位。
例：将二进制的(11010111)B转换为十六进制的步骤如下：
1. 0111 = 7；
2. 1101 = D；
3. 读数，读数从高位到低位，即(11010111)B=(D7)H。
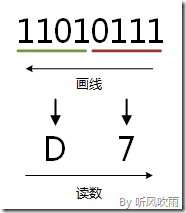
（Figure12：图解二进制 → 十六进制）
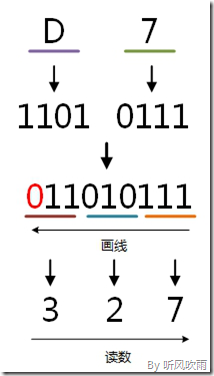
方法：取一分四法，即将一位十六进制数分解成四位二进制数，用四位二进制按权相加去凑这位十六进制数，小数点位置照旧。
例：将十六进制的(D7)H转换为二进制的步骤如下：
1. D = 1101；
2. 7 = 0111；
3. 读数，读数从高位到低位，即(D7)H=(11010111)B。
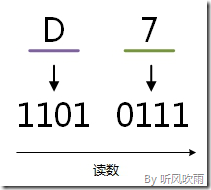
（Figure13：图解十六进制 → 二进制）
(四) （八进制） ↔ （十六进制）
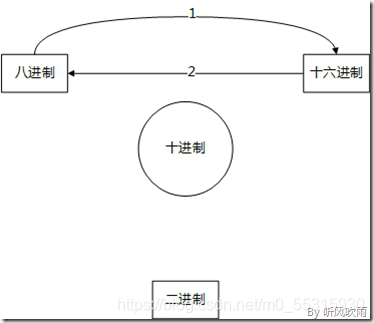
（Figure14：八进制与十六进制之间的转换）
方法：将八进制转换为二进制，然后再将二进制转换为十六进制，小数点位置不变。
例：将八进制的(327)O转换为十六进制的步骤如下：
1. 3 = 011；
2. 2 = 010；
3. 7 = 111；
4. 0111 = 7；
5. 1101 = D；
6. 读数，读数从高位到低位，D7，即(327)O=(D7)H。
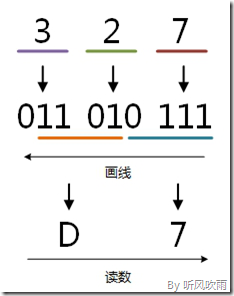
（Figure15：图解八进制 → 十六进制）
方法：将十六进制转换为二进制，然后再将二进制转换为八进制，小数点位置不变。
例：将十六进制的(D7)H转换为八进制的步骤如下：
1. 7 = 0111；
2. D = 1101；
3. 0111 = 7；
4. 010 = 2；
5. 011 = 3；
6. 读数，读数从高位到低位，327，即(D7)H=(327)O。
（Figure16：图解十六进制 → 八进制）
-
进制位算法的案例应用
1.2.1 八进制到十进制的问题
一、问题描述
问题：把一个八进制正整数转化成十进制。
输入：一行，仅含一个八进制表示的正整数a，a的十进制表示的范围是(0, 65536)。
输出：一行，a的十进制表示。
输入样例：11。
输出样例：9。
（问题来源：OpenJ_Bailian - 2735 ）
- 分析设计、解决方法及技术要点
本题属于一个十分简单的进制转化问题，由八进制转换为十进制。
该问题的主要算法应该为八进制的特点是满8进一，所以我们可以根据这一特点。将八进制数分别分离出各个位数。由低位至高位分别乘以8的逐级次幂，在将他们进行一个相加。即可达到本题目标。
Eg：
八进制数 11
转化过程：1*1+1*8=9；
十进制数 9
程序编写过程中有步计算八进制数位数的过程，利用数组和循环等来控制加减次数
三、程序和运行结果
| #include<iostream> #include<cmath> using namespace std; int main() { int j,s,k=0; int a[50]; cin>>s; while(s!=0) { j=s%10;//求s的各个位数 a[k]=j;//将s的各个位数赋值给a[] k=k+1;//计算s是一个几位数 s=s/10; } s=0; for(j=k-1;j>=0;j--) { s=pow(8,j)*a[j]+s; } cout<<s; return 0; } |
运行结果：
一、问题描述
问题：将十进制整数转换成二进制数。
输入：5个整数 n。
输出：对于每个 n，输出 n 值，然后输出 -->，再然后输出二进制数。每个整数 n 的输出，独立占一行。
输入样例： 2
0
-12
1
3
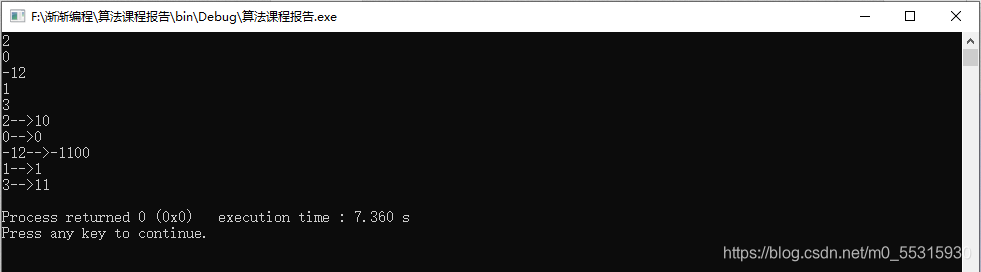
输出样例：2-->10
0-->0
-12-->-1100
1-->1
3-->11
（问题来源：计蒜客 - T1465）
二、分析设计、解决方法及技术要点
该题要求进行五次赋值并且一并输出，这不得不使得我们选择函数的思想解决这个题的问题。首先，我们应该进行一次的十进制转化为二进制的代码的编写。十进制的数转化为二进制的数，运算过程例如10%2=0；我们用数组进行一个存储，在将10/2=5；将5%2=1；在进行存储，再将5/2=2；2%2=1；则输出结果为110；以此类推；可以将此程序写成一个函数。然后在主函数中进行一个调用。在改过程结束之后我发现了0不会进行改程序的执行，所以我将它单独拿了出来，如果输入结果有0，则不进行一个函数的调用。而后，我又发现当输入结果为负数时，结果有点差强人意。所以我又在函数中进行了一个正负数的判断。终究完成了该问题。
三、程序和运行结果
| #include<iostream> using namespace std; int a[1000]; int transform( int n){ int i,j=0; if(n<0) { i=-n; while(i) { a[j]=i%2; i/=2; j++; } cout<<n<<"-->"<<"-"; for(i=j-1;i>=0;i--) cout<<a[i]; cout<<endl; } else { i=n; while(i) { a[j]=i%2; i/=2; j++; } cout<<n<<"-->"; for(i=j-1;i>=0;i--) cout<<a[i]; cout<<endl; } } int main() { int n1,n2,n3,n4,n5; cin>>n1>>n2>>n3>>n4>>n5; if(n1==0) cout<<"0-->0"<<endl; else transform(n1); if(n2==0) cout<<"0-->0"<<endl; else transform(n2); if(n3==0) cout<<"0-->0"<<endl; else transform(n3); if(n4==0) cout<<"0-->0"<<endl; else transform(n4); if(n5==0) cout<<"0-->0"<<endl; else transform(n5); return 0; } |
运行结果：
一、问题描述
问题：输入基数 b 和正整数 n（ b进制），输出 n 的十进制表示.
输入：题目有多组数据。
每组数据是两个整数 b（2≤b≤10）和 n（n<9）。
输出：每组数据输出一行，是转换为十进制之后的数。
输入样例： 2 10010
3 200
4 102
9 20
10 18
输出样例： 18
18
18
18
18
（问题来源：计蒜客 - T1452）
二、分析设计、解决方法及技术要点
此题为一个多种进制混合进行一个转化，咋眼一看很难，因为涉及到了好几个进制位的转换，但该题进行了一个简单化，就是只限定在2--10之内的进制转换，无疑不给我们减小了巨大的难度，所以我们就可以根据题意一步一步来。其中我们需要会的主要算法为
int sum=0,i=1;
while(n){
int k;
a=n%10;
n/=10;
k=i*a;
sum=sum+k;
i=i*b;
}
这是一个很简单的运算，相必刚才那么难的都会了，这么简单的就不用多说了吧。我们只需要将这段程序加个while循环，进行一个多组输入的效果，本题即可完成。
三、程序
| #include<iostream> using namespace std; int main() { int b,n,a; while(cin>>b>>n){ int sum=0,i=1; while(n){ int k; a=n%10; n/=10; k=i*a; sum=sum+k; i=i*b; } cout<<sum; } return 0; } |
运行结果：
一、问题描述
问题： 这是一个疯狂的进制转换问题，你需要把一个2到16进制之间某个进制的数字转换为一个十进制数！
输入：本题有多组测试数据，对于每组数据输入两个数m和n，m表示这个数的是几进制的，n表示这个数，输入处理到文件结束（保证这个数在32位有符号整数范围内）。
输出： 对于每组测试数据输出对应的十进制数并换行。
输入样例： 8 10
16 A
16 Ac
输出样例：8
10
172
（问题来源：HRBUST - 1896）
二、分析设计、解决方法及技术要点
我查询了一下资料后得以解决这个问题：
根据这个写的解释写出代码成果。
三、程序和运行结果
| #include<cstdio> #include<cstring> int toInt(char a) { if(a >= '0' && a <= '9') return a - '0'; else if(a >= 'a' && a <= 'f') return a - 'a' + 10; // 小写 else return a - 'A' + 10; // 大写 } char toChar(int x) { if(x >= 0 && x <= 9) return '0' + x; else return 'A' + x - 10; } int main() { int a, b=10; char s[50]; while((scanf("%d%s", &a, s) != EOF)) { // 先转换为十进制 int y = 0; // y存十进制数 int product = 1; // product在循环中会不断乘P,得到1、P、P^2 for(int i = strlen(s) - 1; i >= 0; i--) { y += toInt(s[i]) * product; product = product * a; } //再转换为b进制 char ans[100], num = 0; // num为位数 do { ans[num++] = toChar(y % b); y /= b; } while(y != 0); for(int i = num - 1; i >= 0; i--) { printf("%c", ans[i]); } printf("\n"); } } |
运行结果：
一、问题描述
问题： 进制转换是一个疯狂的问题，你需要将一个整数转化为32位的二进制形式。
输入： 本题有多组测试数据，对于每组数据输入一个正整数number，number不超过32位有符号整数的最大值，输入到文件结束。
输出： 对于每组数据输出一个对应的32位二进制字符串并换行。
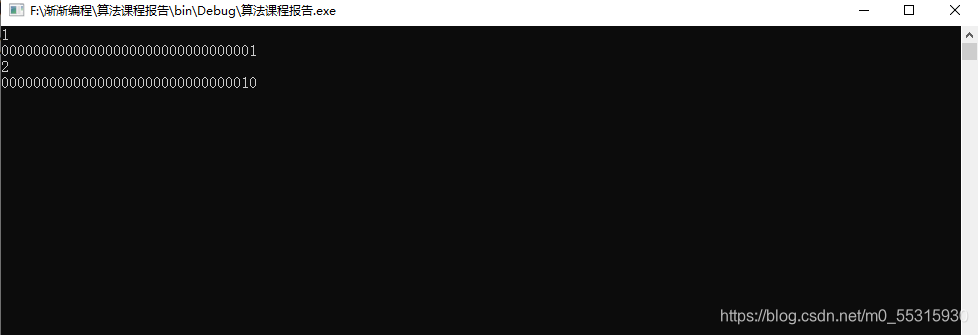
输入样例： 1
2
输出样例：00000000000000000000000000000001
00000000000000000000000000000010
（问题来源：HRBUST - 1899）
二、分析设计、解决方法及技术要点
该题为上题的进化版，看似很难很复杂，但是仔细阅读就会发现，无非就是又考了一遍十进制转化为二进制，而且比第二题更加简单，只需要将数组设置长度为32，在最后十进制转化为二进制的算法执行完毕之后，将数组定义在全局，会使数组中没有赋值的数组自动化为0，然后从后往前全部输出。此题即可解决。
三、程序和运行结果
| #include<iostream> using namespace std; int a[31]; int main() { int n; while(cin>>n){ int i,j=0; i=n; while(i) { a[j]=i%2; i/=2; j++; } for(i=31;i>=0;i--) cout<<a[i]; cout<<endl; } return 0; } |
运行结果：
答题地址网站：https://vjudge.net/contest/443220
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
