最小生成树算法（Prim和Kruskal的详细实现）

最小生成树（Minimum Spanning Tree, MST）是图论中的一个重要概念，它是指在一个加权连通图中，找到一棵包含所有顶点的生成树，使得这棵树的所有边的权重之和最小。常见的算法有普里姆算法（Prim）和克鲁斯卡尔算法（Kruskal）。举个具体的实例：各个村落会修路，每条路的成本，因此需要计划出一种方案使得成本最低。

1、Prim算法

普里姆算法是一种贪心算法，从一个顶点开始，逐步扩展生成树，每次选择权重最小的边加入生成树。

下面给出一个具体的步骤：

（1）例如下面一个有四个节点的图，visited代表是否已经加入最小生成树，min_edge表示该节点与最小生成这个连通图的最小距离，parent代表这个最小距离所连接的父节点

（2）一开始从任意节点（一般是V0节点）开始，加入最小生成树，然后与V0相连的V1和V3更新min_edge和parent

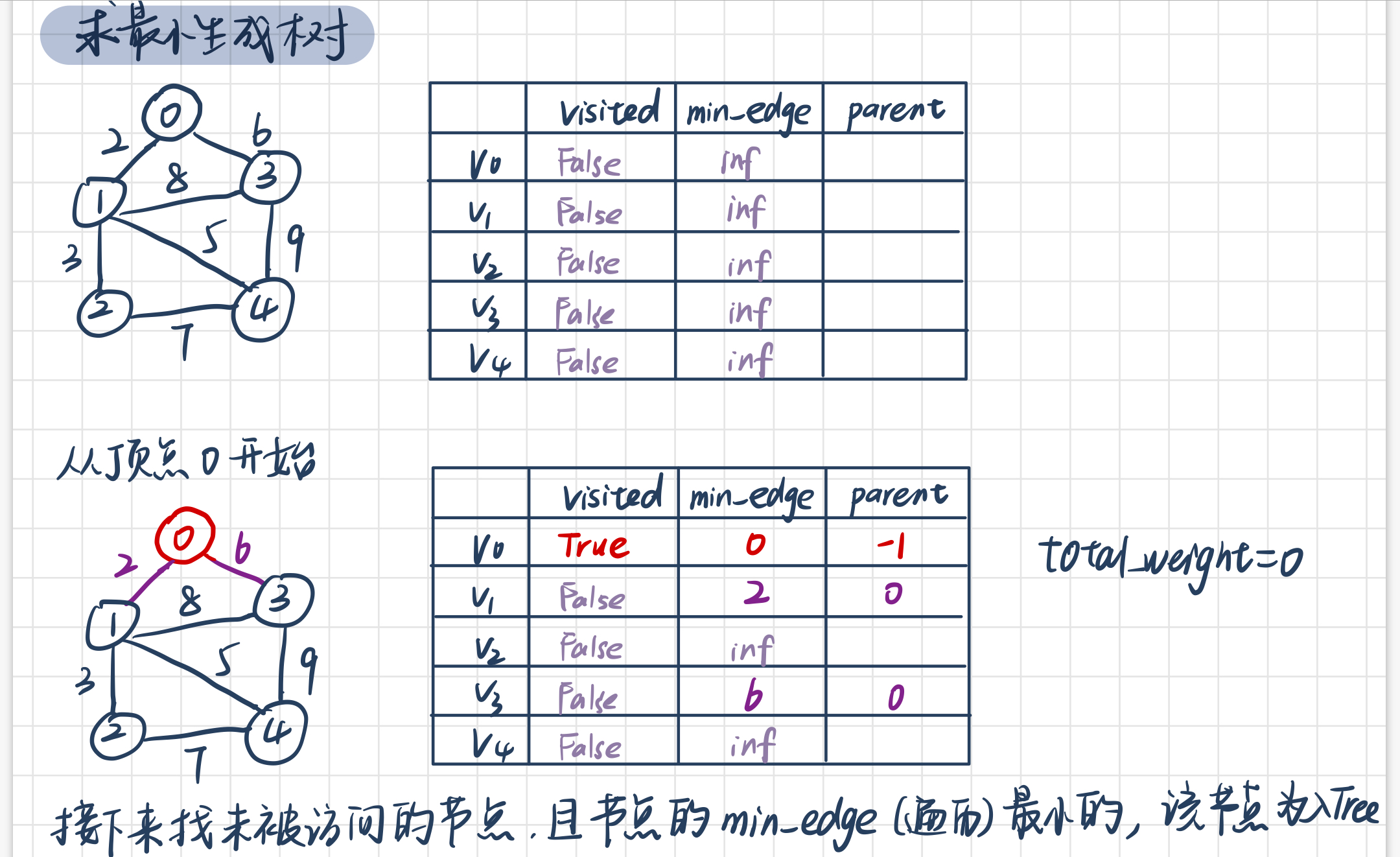
（3） 找到min_edge中的最小边，将节点加入最小生成树，这里min_edge最小为2，因此加入V1节点，然后总权重为2

（4）当加入V1后，去遍历所有节点，看是否能更新min_edge，更新完成之后更新parent为V1

（5）继续重复上述步骤

 

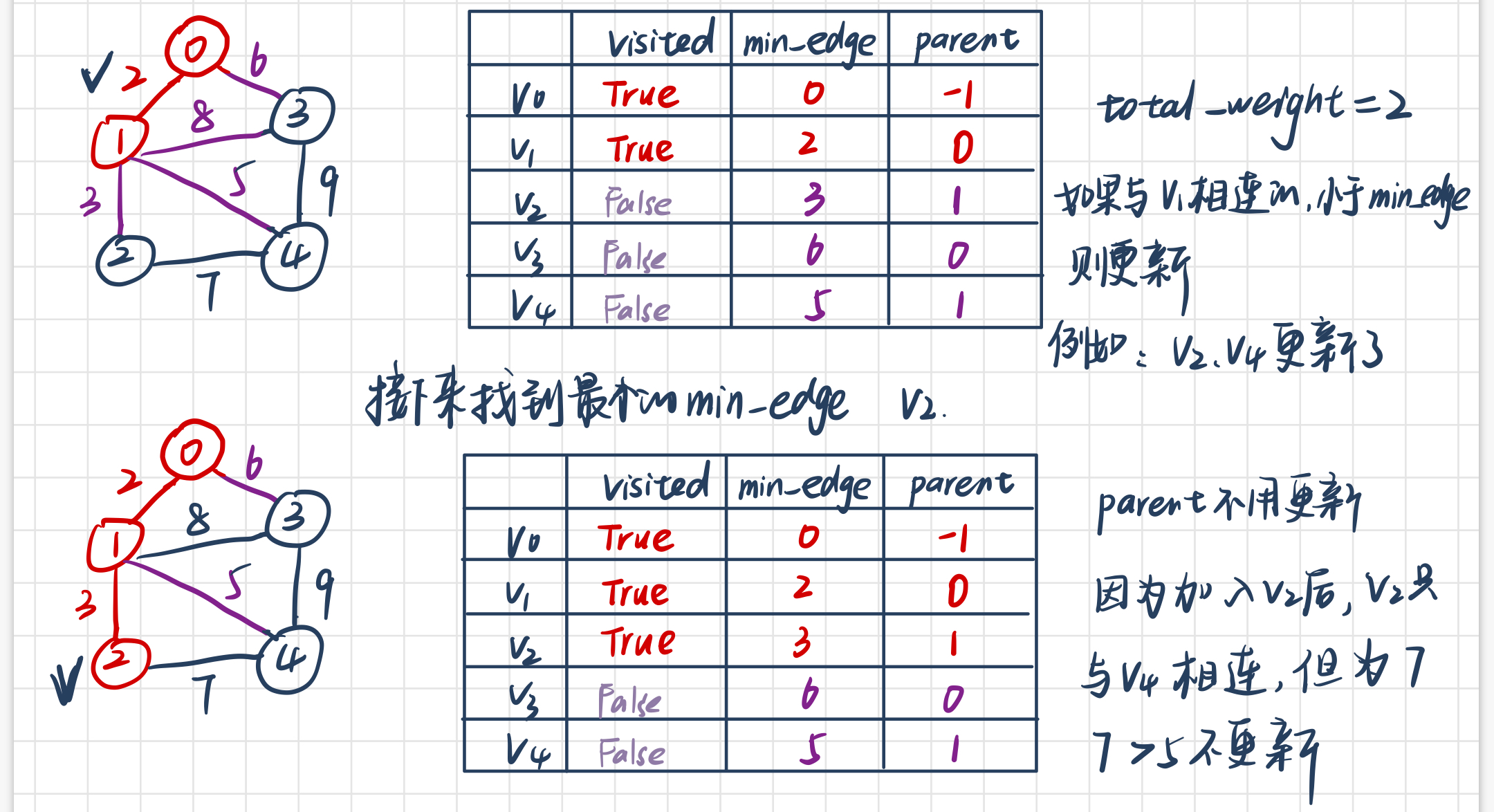
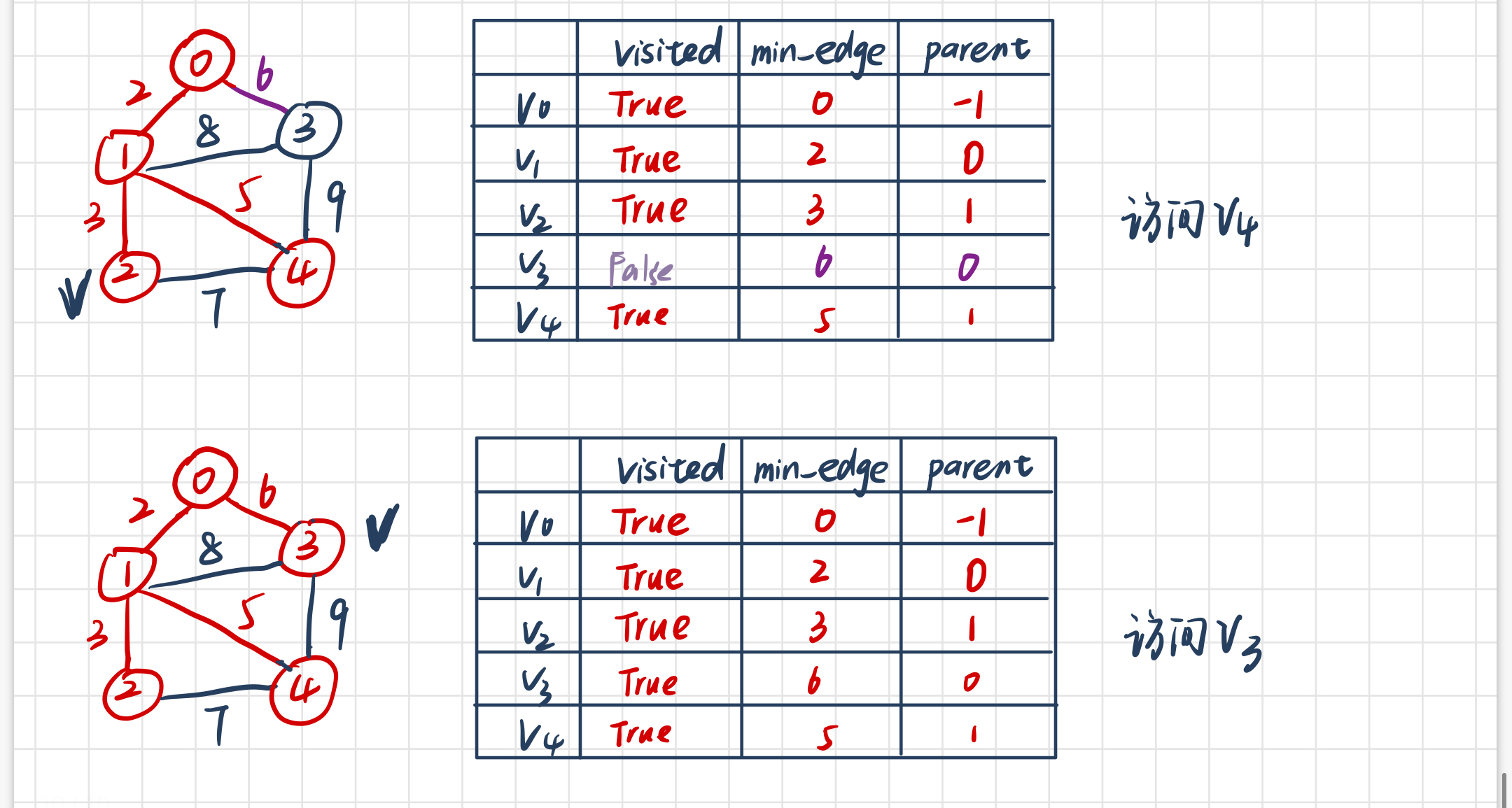
算法的python实现：

def prim(graph):
    """
    使用普里姆算法生成最小生成树，不使用 heapq
    :param graph: 图的邻接矩阵表示
    :return: 最小生成树的边和总权重
    """
    n = len(graph)  # 顶点数量
    visited = [False] * n  # 标记顶点是否访问过
    min_edge = [float("inf")] * n  # 记录每个顶点到生成树的最小边权重
    parent = [None] * n  # 记录每个顶点的父节点
    mst = []  # 存储最小生成树的边
    total_weight = 0  # 最小生成树的总权重

    # 从顶点 0 开始
    min_edge[0] = 0
    parent[0] = -1

    for _ in range(n):
        # 找到未访问的最小边权重的顶点
        u = None
        min_val = float("inf")
        for i in range(n):
            if not visited[i] and min_edge[i] < min_val:
                u = i
                min_val = min_edge[i]

        visited[u] = True  # 标记顶点 u 为已访问
        if parent[u] is not None:
            mst.append((parent[u], u, min_edge[u]))
            total_weight += min_edge[u]

        # 更新与顶点 u 相连的顶点的最小边权重
        for v in range(n):
            if not visited[v] and graph[u][v] > 0 and graph[u][v] < min_edge[v]:
                min_edge[v] = graph[u][v]
                parent[v] = u

    return mst, total_weight


# 示例：邻接矩阵表示的图
graph = [
    [0, 2, 0, 6, 0],
    [2, 0, 3, 8, 5],
    [0, 3, 0, 0, 7],
    [6, 8, 0, 0, 9],
    [0, 5, 7, 9, 0]
]

mst, total_weight = prim(graph)
print("最小生成树的边：", mst)
print("最小生成树的总权重：", total_weight)

 2、Kruskal算法

Kruskal算法也是基于贪心思想，通过选择权重最小的边逐步构建最小生成树，同时使用并查集来避免环的出现。

class UnionFind:
    def __init__(self, n):
        self.parent = list(range(n))
        self.rank = [0] * n # 每棵树的秩（高度）

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x != root_y:
            # 用于调整树
            if self.rank[root_x] > self.rank[root_y]:
                self.parent[root_y] = root_x
            elif self.rank[root_x] < self.rank[root_y]:
                self.parent[root_x] = root_y
            else:
                self.parent[root_y] = root_x
                self.rank[root_x] += 1
            return True
        return False


def kruskal(edges, n):
    """
    使用克鲁斯卡尔算法生成最小生成树，不使用 heapq
    :param edges: 图的边列表，格式为 [(权重, 顶点1, 顶点2)]
    :param n: 顶点数量
    :return: 最小生成树的边和总权重
    """
    edges.sort()  # 按权重从小到大排序
    uf = UnionFind(n)
    mst = []
    total_weight = 0

    for weight, u, v in edges:
        if uf.union(u, v):  # 如果加入这条边不会形成环
            mst.append((u, v, weight))
            total_weight += weight

    return mst, total_weight


# 示例：边列表表示的图
edges = [
    (2, 1, 2),
    (3, 2, 3),
    (5, 2, 5),
    (6, 1, 4),
    (7, 3, 5),
    (8, 2, 4),
    (9, 4, 5)
]
n = 5  # 顶点数量

mst, total_weight = kruskal(edges, n)
print("最小生成树的边：", mst)
print("最小生成树的总权重：", total_weight)

---

都看到这里了，给个小心心呗~♥