基于Open-CV的多四边形检测方案

一、设计目标

对于一个含有多个相邻四边形的图片，定位出其中每一个四边形的顶点。典型的案例如一个围棋棋盘，可以定位出所有的格子的点。

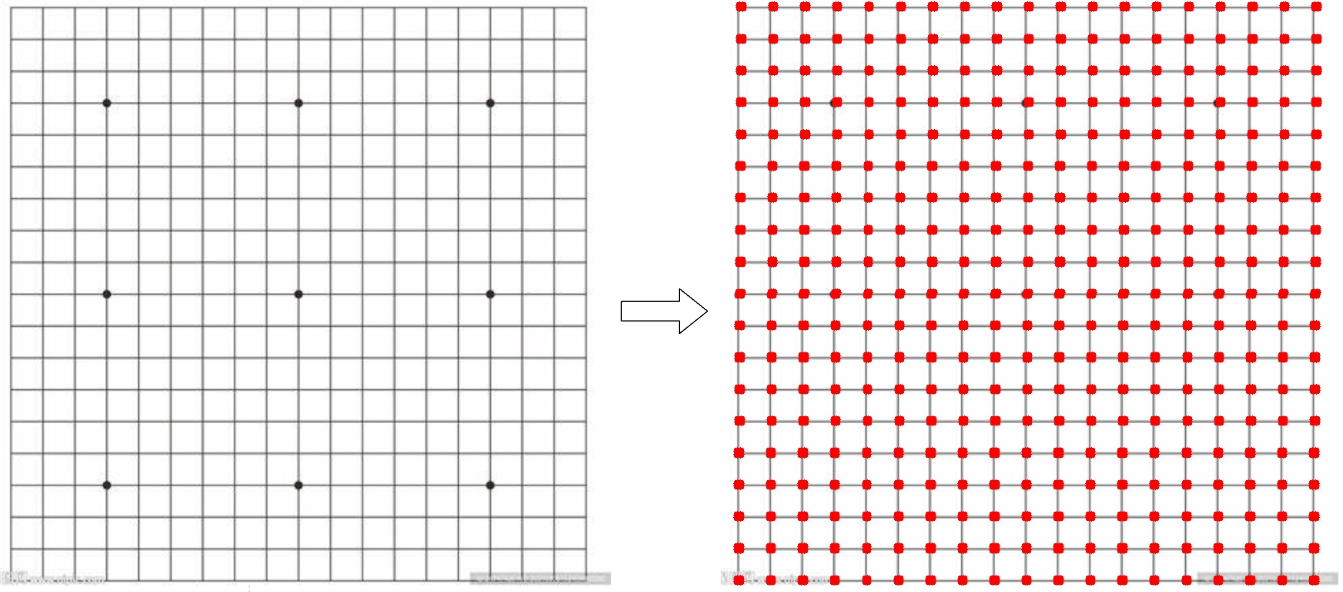
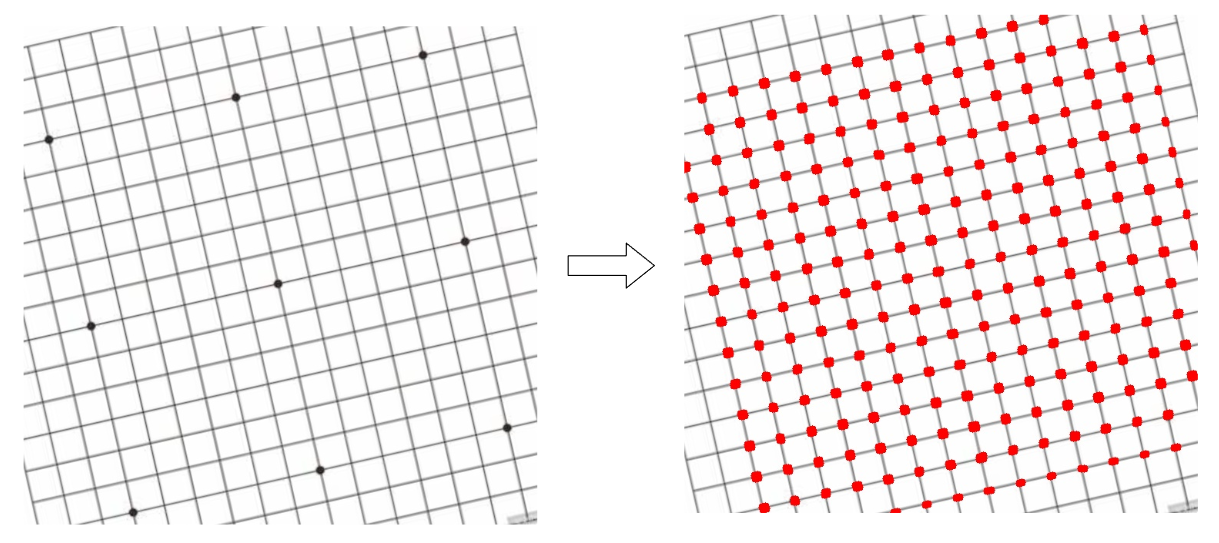
软件工具：

Python==3.9
opencv-python==4.10.0.84
numpy==1.22.4

二、工作流程

1. 将输入图像转化为灰度值，并进行高斯滤波与Canny边缘检测
2. 对图像进行霍夫变化，捕获图像中的直线
3. 过滤霍夫变换的结果定位边框，给出定位点

三、图像预处理

首先是载入图像，并进行简单的预处理，包括转化为灰度、高斯滤波、边缘检测：

import cv2
# 读取图片
orignal_img = cv2.imread(img_path)
# 简单预处理
imgGray = cv2.cvtColor(orignal_img, cv2.COLOR_RGB2GRAY)
imgBlur = cv2.GaussianBlur(imgGray, (5, 5), 1)
imgCanny = cv2.Canny(imgBlur, 60, 60)
# 显示
cv2.imshow("Original Image", orignal_img)
cv2.imshow("Gray Image", imgGray)
cv2.imshow("GaussianBlur Image", imgBlur)
cv2.imshow("Edge Image", imgCanny)
k = cv2.waitKey(0)

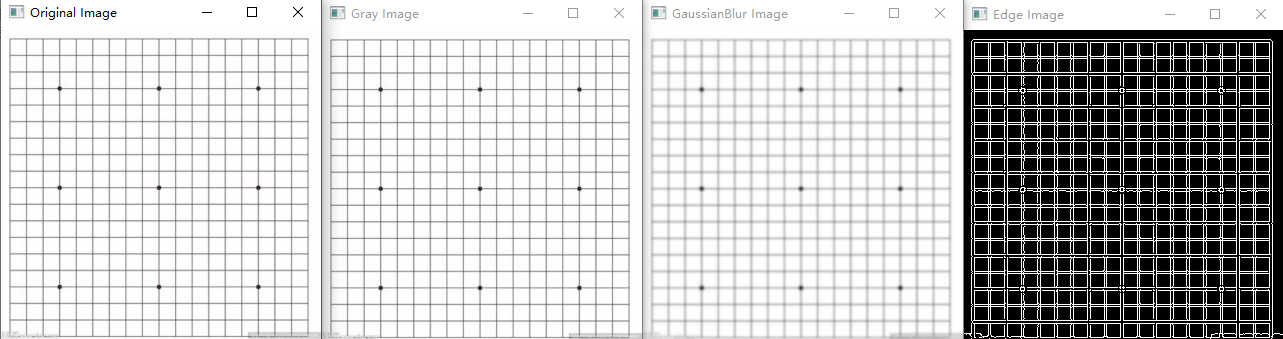
然后进行霍夫变换，霍夫变化用于检测矩形框构成的直线:

# img_org：原始图片
# img_edge：进行边缘检测后的图片
def get_hough_res(img_org, img_edge):
    imgLines = img_org.copy()
    # 霍夫变换
    lines = cv2.HoughLines(img_edge, 1, np.pi / 180, 200, 300, 5)
    # 计算坐标并绘制
    for line in lines:
        rho = line[0][0]
        theta = line[0][1]
        a = np.cos(theta)
        b = np.sin(theta)
        x0 = a * rho
        y0 = b * rho
        x1 = int(x0 + 1000 * (-b))
        y1 = int(y0 + 1000 * (a))
        x2 = int(x0 - 1000 * (-b))
        y2 = int(y0 - 1000 * (a))

        cv2.line(imgLines, (x1, y1), (x2, y2), (0, 0, 255), 2)
    return imgLines

imgHough = get_hough_res(orignal_img, imgCanny)

cv2.imshow("Orginal Image", orignal_img)
cv2.imshow("Hough Image", imgHough)
cv2.waitKey(0)

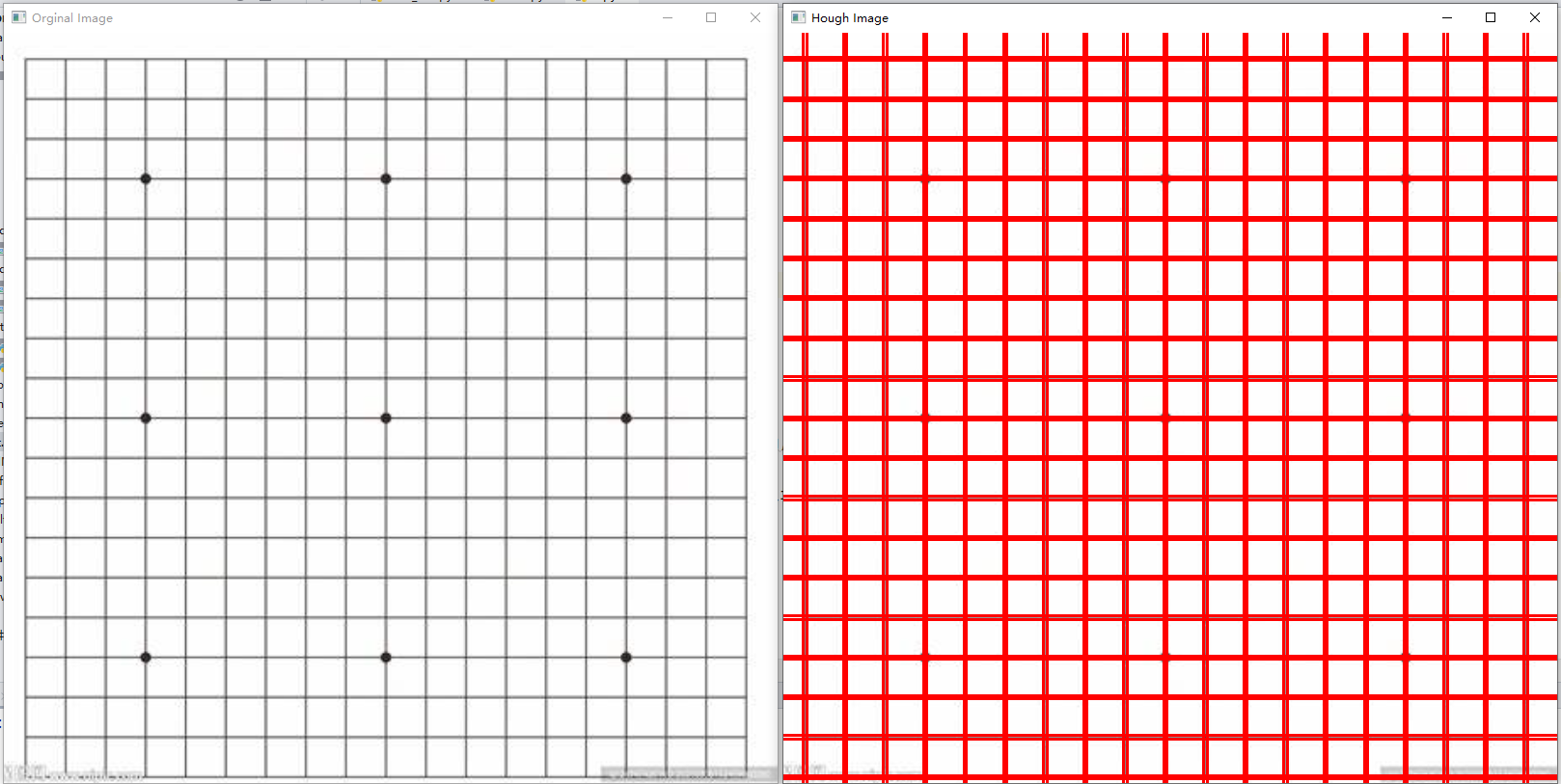
四、直线过滤

可以看出，霍夫变换的结果有很多重复划定的直线，这不利于我们进行处理划分矩形的边缘并定位四边形。因此，需要将相似位置的线去除。

对于两条直线，我们判断他们相似的依据是比较他们的斜率$k$和截距$b$。霍夫变换得到的是一条直线的两个点，因此我们首先将点换算为斜率$k$和截距$b$：

# 已知直线上两点(x1, y1)和(x2, y2)，计算直线的斜率k和截距b
def calculate_slope_and_intercept(x1, y1, x2, y2):
    k = (y2 - y1) / (x2 - x1 + 1)
    if k < -200:
        k = -200
    b = y1 - k * x1
    return k, b

但是直线的斜率依然不便于比较，当直线的角度过大的是，1°的差距可能导致极大的斜率数值变化。因此，我们使用$arctan(\cdot )$函数将直线的斜率转换回角度：

# 转换为角度
def convert_slope_to_angle(x):
    y = math.degrees(math.atan(x))
    return y

这样我们就能通过比较斜率和直线距离的方式来对直线进行过滤，过滤方法：

1. 使用一个list对象line_list存放过滤结果

2. 遍历霍夫变换得到的直线：

   • 对于第一条直线，直接选用

   • 对于后续直线，与line_list的直线进行比较：如果有相似直线则舍弃本直线，否则选用本直线

代码如下：

# 霍夫变换
lines = cv2.HoughLines(img_edge, 1, np.pi / 180, 200, 200, 5)

# 记录直线信息: (斜率，截距)
line_list = []
# 遍历霍夫变换得到的直线
for line in lines:
    rho = line[0][0]
    theta = line[0][1]
    # 计算直线中两点的坐标
    x1, y1, x2, y2 = calculate_coordinate(rho, theta)

    # 计算这条直线的斜率
    k_now, b_now = calculate_slope_and_intercept(x1, y1, x2, y2)
    # 将斜率转化回角度
    angle_of_k_now = convert_slope_to_angle(k_now)

    if len(line_list) == 0:  # 第一条直线直接加入
        line_list.append((k_now, b_now))
    else:  # 后续直线进行判断
        add_flag = 1
        # 对已经选取的直线进行遍历
        for i, (k, b) in enumerate(line_list):
            # 将斜率转化回角度
            angle_of_k = convert_slope_to_angle(k)
            # 如果有角度相近的直线，就进行距离比较
            if abs(angle_of_k_now - angle_of_k) <= threshold_k:
                # 寻找同方向的线中是否有相似位置的线
                d1 = calculate_distance_to_line(x1, y1, k, b)
                d2 = calculate_distance_to_line(x2, y2, k, b)
                if d1 < threshold or d2 < threshold:
                    add_flag = 0
        # 如果现有信息中，不存在相似的直线，则添加当前线
        if add_flag:
            line_list.append((k_now, b_now))

# 在图片中标定直线
for (k, b) in line_list:
    drawline(img_lines, k, b)

五、确定交点

过滤得到矩形边框对应的直线后，只需要进行进行直线的两两相交即可得到交点。

由于我们存储的是直线的斜率和截距信息，可以通过下面的方法计算交点。

# 已知两条直线的斜率k和截距b，求交点
def find_intersection(k1, b1, k2, b2):
    # 检查斜率是否相等，如果相等，直线可能平行或重合
    if k1 == k2:
        if b1 == b2:
            return -1, -1
        else:
            return -1, -1
    x = (b2 - b1) / (k1 - k2)
    y = int(k1 * x + b1)
    x = int(x)

    return x, y

那么，接下来就是简单轻松的两两求交点环节：

# 直线两两求交点
def find_all_intersections(img, line_list):
    height, width = img.shape[:2]
    intersections = []
    num_lines = len(line_list)
    # 直线两两求交
    for i in range(num_lines):
        for j in range(i + 1, num_lines):
            k1, b1 = line_list[i]
            k2, b2 = line_list[j]
            # 只对斜率差别很大的直线进行求交点
            if abs(convert_slope_to_angle(k1) - convert_slope_to_angle(k2)) >= 45:
                # 已知两条直线的斜率k和截距b，求交点
                x, y = find_intersection(k1, b1, k2, b2)
                # 记录在图片坐标范围内的点
                if 0 <= x <= width-1 and 0<= y <= height -1:
                    intersections.append((x, y))
    return intersections

# 在图片中标定交点
for x, y in intersections:
    cv2.circle(img_intersection, (x, y), radius=5, color=(0, 0, 255), thickness=-1)

六、工程源码

• github: Rectangle-Detection