wy的leetcode刷题记录_Day87

wy的leetcode刷题记录_Day87

声明

本文章的所有题目信息都来源于leetcode
如有侵权请联系我删掉!
时间：2024-3-14

前言

2789. 合并后数组中的最大元素

今天的每日一题是：2789. 合并后数组中的最大元素

题目介绍

给你一个下标从 0 开始、由正整数组成的数组 nums 。

你可以在数组上执行下述操作 任意 次：

• 选中一个同时满足 0 <= i < nums.length - 1 和 nums[i] <= nums[i + 1] 的整数 i 。将元素 nums[i + 1] 替换为 nums[i] + nums[i + 1] ，并从数组中删除元素 nums[i] 。

返回你可以从最终数组中获得的 最大 元素的值。

示例 1：

输入：nums = [2,3,7,9,3]
输出：21
解释：我们可以在数组上执行下述操作：

• 选中 i = 0 ，得到数组 nums = [5,7,9,3] 。
• 选中 i = 1 ，得到数组 nums = [5,16,3] 。
• 选中 i = 0 ，得到数组 nums = [21,3] 。 最终数组中的最大元素是 21 。可以证明我们无法获得更大的元素。

示例 2：

输入：nums = [5,3,3]
输出：11
解释：我们可以在数组上执行下述操作：

• 选中 i = 1 ，得到数组 nums = [5,6] 。
• 选中 i = 0 ，得到数组 nums = [11] 。 最终数组中只有一个元素，即 11 。

思路

很明显这道题应该从后往前遍历，如果从前往后遍历的话假设有2，3，4这个序列那么经过一次遍历将会变成5，4最大值为5，发现5（前两个元素的和）和4不能合并，而实际上题目并没有给出合并的顺序，于是为了获得最大元素的值，我们用贪心的想法，如果有一个升序序列a,b,c我们从后往前遍历，因为c>b>a，所以c+b>a也是一定成立的，最后这个序列将合并成a+b+c得到最优解。这里有几个小细节：一开始我是按照题目来将nums[i]=nums[i]+nums[i+1]这样有可能超过int表示的范围，于是我只用一个long long的变量来维护合并序列之和。

代码

class Solution {
public:
    long long maxArrayValue(vector<int>& nums) {
        //从后向前合并
        int n=nums.size();
        long long maxn=nums[0];
        long long sum=nums[n-1];
        for(int i=n-2;i>=0;i--)
        {
            if(nums[i]<=sum)
            {
                sum+=nums[i];               
            }
            else
            {
                sum=nums[i];
            }
             maxn=max(maxn,sum);
        }
        return maxn;
    
    }
};

收获

算是我做的较快的题了，这几天刷题手感上来了。

54. 螺旋矩阵

54. 螺旋矩阵

题目介绍

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

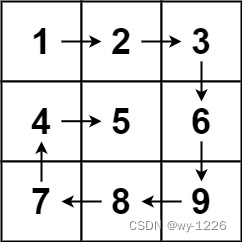
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

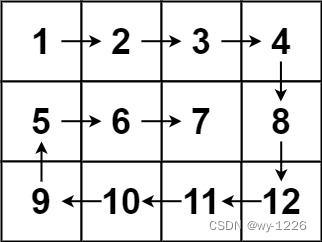
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

思路

模拟：分别从左向右、从上向下、从右向左和从下向上进行遍历，这里我们初始化四个边界left、right、top、bottom当边界相交时表示已全部顺时针串成。

代码

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int n=matrix.size();//行
        int m=matrix[0].size();//列
        vector<int> ans;
        int left=0,right=m-1;
        int top=0, bottom=n-1;
        while(1)
        {
            for(int i=left;i<=right;i++)
            {
                ans.emplace_back(matrix[top][i]);
            }
            if(++top>bottom)    break;
            for(int i=top;i<=bottom;i++)
            {
                ans.emplace_back(matrix[i][right]);
            }
            if(--right<left)   break;
            for(int i=right;i>=left;i--)
            {
                ans.emplace_back(matrix[bottom][i]);
            }
            if(--bottom<top)    break;
            for(int i=bottom;i>=top;i--)
            {
                ans.emplace_back(matrix[i][left]);
            }
            if(++left>right)   break;
        }
        return ans;

        return ans;
    }
};

收获

看到这道题就有点眼熟，大一的时候数据结构老师曾经给我们出过这道题，当时也是想着用循环模拟但是思路非常粗造，代码手法也很拉，以至于没写出来去抄题解。虽然但是现在也是看了题解的手法才写的比较容易看懂哈哈哈。

48. 旋转图像

48. 旋转图像

题目介绍

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

思路

真烦真烦真烦，看了题解恍然大悟，各位可以先自己在草稿纸上举个例子（实际上是我懒得画图），先将矩阵进行转置然后再逐行逆置即可。
然后再说正常人解法：观察矩阵（请自行在草稿纸上进行推导），选取矩阵中任意一个点，发现其四次旋转后回到原点，对于题目中不让用额外的矩阵空间所以我们没法解决matrix[row][col]=matrix[col][n-row-1]被覆盖的问题，又因为矩阵上某四个点为一循环，所以我们只需要一个变量来记录其中被覆盖的值完成这个循环即可。

代码

class Solution {
public:

    void reverse(vector<int>& a)
    {
        int n=a.size();
        for(int i=0;i<n/2;i++)
        {
            swap(a[i],a[n-i-1]);
        }
    }
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        for(int i=0;i<n;i++)
        {
            for(int j=i;j<n;j++)
            {
                swap(matrix[i][j],matrix[j][i]);
            }
        }
        for(int i=0;i<n;i++)
        {
            reverse(matrix[i]);
        }
    }
};

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n=matrix.size();
        for(int i=0;i<n/2;i++)
        {
            for(int j=0;j<(n+1)/2;j++)
            {
                int temp=matrix[i][j];
                matrix[i][j] = matrix[n - j - 1][i];
                matrix[n - j - 1][i] = matrix[n - i - 1][n - j - 1];
                matrix[n - i - 1][n - j - 1] = matrix[j][n - i - 1];
                matrix[j][n - i - 1] = temp;

            }
        }
    }
};

收获

收获了什么？收获了如何快速看题解！！

240. 搜索二维矩阵 II

240. 搜索二维矩阵 II

题目介绍

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]],target = 20
输出：false

思路

这道题仔细观察矩阵你会发现从矩阵右上角往左下看其实是一个搜索二叉树，以此便可查询…

代码

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int n=matrix.size();
        int m=matrix[0].size();
        int mid=0;
        int row=0;int col=m-1;
        while(1)
        {
            if(row>=n||col<0)   break;
            mid=matrix[row][col];
            if(target>mid)
            {
                row++;
            }
            else if(target<mid)
            {
                col--;
            }
            else{
                return true;
            }
        }
        return false;
    }
};

收获

226. 翻转二叉树

226. 翻转二叉树

题目介绍

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

思路

递归，将右节点接到左指针同理左节点接到右指针上。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(!root)   return nullptr;
        TreeNode *newTree=new TreeNode(root->val);
        newTree->left=invertTree(root->right);
        newTree->right=invertTree(root->left);

        return newTree;
    }
};

收获

无

101. 对称二叉树

101. 对称二叉树

题目介绍

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

思路

递归的判断左子树是否与右子树对称，对称就是值，左子树的左节点与右子树的右节点相同切左子树的右节点与右子树的左节点相同，但凡有一个不同就不行。

代码

递归解法：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool dfs(TreeNode* left,TreeNode* right)
    {
        if(left==nullptr&&right==nullptr)
            return true;
        if(left==nullptr||right==nullptr)
            return false;
        if(left->val!=right->val)
            return false;
        return dfs(left->right,right->left)&&dfs(left->left,right->right);
    }
    bool isSymmetric(TreeNode* root) {
        if(!root)
            return true;
        return dfs(root->left,root->right);
    }
};

递推解法（BFS）：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        queue<TreeNode*> q;
        if(root==nullptr)
            return true;
        if(root->left==nullptr&&root->right==nullptr)
            return true;

        q.push(root->left);
        q.push(root->right);
        while(!q.empty())
        {
            TreeNode* lleft=q.front();
            q.pop();
            TreeNode* rright=q.front();
            q.pop();
            if(lleft==nullptr&&rright==nullptr)
                continue;
            if(lleft==nullptr||rright==nullptr)
                return false;
            
            if(lleft->val!=rright->val)
                return false;
            // if(lleft->)
            q.push(lleft->left);
            q.push(rright->right);
            q.push(lleft->right);
            q.push(rright->left);
        }
        return true;
    }
};

收获

递归是真的很难写，一看就会一写就废，看到评论区的大佬试图教会我如何写递归看的心累…（找递归点和递归条件）

98. 验证二叉搜索树

98. 验证二叉搜索树

题目介绍

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

输入：root = [2,1,3]
输出：true

示例 2：

输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

思路

已知二叉搜索树的中序遍历序列是升序序列，于是用中序遍历获得其序列最后检验是否呈升序即可。

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> a;
    void dfs(TreeNode* node)
    {
        if(node==nullptr)
            return ;
        dfs(node->left);
        a.emplace_back(node->val);
        dfs(node->right);
    }
    bool isValidBST(TreeNode* root) {
        dfs(root);
        int n=a.size();
        for(int i=1;i<n;i++)
        {
            if(a[i]<=a[i-1])
                return false;
        }
        return true;
    }
};

收获

无