二叉树高度计算方法

最新推荐文章于 2025-03-23 15:29:59 发布
最新推荐文章于 2025-03-23 15:29:59 发布
阅读量1.3k 收藏 2
点赞数 1
分类专栏： 数据结构 文章标签： 算法 c++ 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/m0_53387935/article/details/130869383
版权
文章介绍了计算二叉树高度的三种方法：递归法、叶子反根法（递归和非递归）以及最大栈法（数组和链表栈）。每种方法都通过示例代码详细解释了其工作原理，如递归法通过比较左右子树的高度，叶子反根法从叶子节点向上找到根节点计数，最大栈法通过维护栈内元素个数来确定树的最大深度。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

二叉树高度计算方法

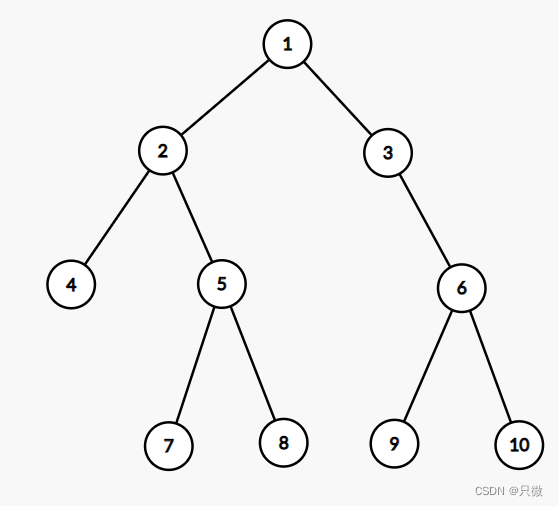
在这里插入图片描述

二叉树的高度-递归法

#include <iostream>
#include <cstdio>

using namespace std;

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空 
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));


    return 0;
}

叶子反根法递归代码

  • 非递归思路：叶子节点的特点是左右节点都是NULL，找到叶子节点，通过叶子节点的pFaher指针向上找
#include <iostream>
#include <cstdio>
#include <malloc.h>

using namespace std;

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

// 链表结构的栈 尾添加尾删除 双向带空头链表
// 栈节点
struct stack {
    struct treeNode *node; // 指向树的节点
    struct stack *pre; // 指向前一个节点
    struct stack *next; // 指向下一个节点
};
struct stack head; // 空头
struct stack *stacktop = &head; // 栈顶指针

// 入栈 链表尾添加
void push(struct treeNode *node) {
    // 申请节点 并且成员赋值
    struct stack *temp = (struct stack *)malloc(sizeof(struct stack));
    if (NULL == temp) {
        return ;
    }
    // 赋初值
    temp->pre = NULL;
    temp->next = NULL;
    temp->node = node;
    // 尾巴连接
    stacktop->next = temp;
    temp->pre = stacktop;
    // 栈顶指针后移
    stacktop = stacktop->next;
}

// 出栈 双向链表尾删除
struct treeNode *pop(void) {
    if (stacktop == &head) {
        // 栈空
        return NULL;
    }
    struct treeNode *temp = stacktop->node; // 得到栈顶的树节点

    stacktop = stacktop->pre; // 节点前移
    free(stacktop->next); // 释放节点
    stacktop->next = NULL; // 新尾指针指向空
    return temp;
}

/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

// 思路类似于前序遍历的 非递归
int Look(struct treeNode *root) {
    struct treeNode *t = root;
    int max = 0; // 记录最大层
    while (1) {
        // 左子树入栈并输出
        while (t != NULL) {
            push(t); // 入栈
            t = t->pLeft;
        }
        if (stacktop == &head) // 栈里面什么都没有
            break;
        t = pop(); // 出栈
        if (NULL == t->pLeft && NULL == t->pLeft) {
            // 判断是否是叶子节点
            int ce = 0;
            struct treeNode *reaf = t;
            while (reaf) {
                // 向上遍历找到root
                ce++;
                reaf = reaf->pFather;
            }
            if (ce > max) {
                max = ce;
            }
        }
        t = t->pRight;
    }
    return max;
}
int max_ce = 0;

void Look2(struct treeNode *root) {
    if (NULL == root) {
        return;
    }
    Look2(root->pLeft); // 左子树入栈
    if (NULL  == root->pLeft && NULL == root->pRight) {
        int cen = 0;
        struct treeNode *reaf = root;
        while(reaf != NULL) {
            cen++;
            reaf = reaf->pFather;
        }
        if (cen > max_ce) {
            max_ce = cen;
        }
    }
    Look2(root->pRight); // 右子树入栈
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));
    Look2(&t1);
    printf("叶子反根递归:%d\n", max_ce);
    printf("叶子反根非递归:%d\n", Look(&t1));


    return 0;
}

叶子反根法非递归代码

#include <iostream>
#include <cstdio>
#include <malloc.h>

using namespace std;

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

// 链表结构的栈 尾添加尾删除 双向带空头链表
// 栈节点
struct stack {
    struct treeNode *node; // 指向树的节点
    struct stack *pre; // 指向前一个节点
    struct stack *next; // 指向下一个节点
};
struct stack head; // 空头
struct stack *stacktop = &head; // 栈顶指针

// 入栈 链表尾添加
void push(struct treeNode *node) {
    // 申请节点 并且成员赋值
    struct stack *temp = (struct stack *)malloc(sizeof(struct stack));
    if (NULL == temp) {
        return ;
    }
    // 赋初值
    temp->pre = NULL;
    temp->next = NULL;
    temp->node = node;
    // 尾巴连接
    stacktop->next = temp;
    temp->pre = stacktop;
    // 栈顶指针后移
    stacktop = stacktop->next;
}

// 出栈 双向链表尾删除
struct treeNode *pop(void) {
    if (stacktop == &head) {
        // 栈空
        return NULL;
    }
    struct treeNode *temp = stacktop->node; // 得到栈顶的树节点

    stacktop = stacktop->pre; // 节点前移
    free(stacktop->next); // 释放节点
    stacktop->next = NULL; // 新尾指针指向空
    return temp;
}

/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

// 思路类似于前序遍历的 非递归
int Look(struct treeNode *root) {
    struct treeNode *t = root;
    int max = 0; // 记录最大层
    while (1) {
        // 左子树入栈并输出
        while (t != NULL) {
            push(t); // 入栈
            t = t->pLeft;
        }
        if (stacktop == &head) // 栈里面什么都没有
            break;
        t = pop(); // 出栈
        if (NULL == t->pLeft && NULL == t->pLeft) {
            // 判断是否是叶子节点
            int ce = 0;
            struct treeNode *reaf = t;
            while (reaf) {
                // 向上遍历找到root
                ce++;
                reaf = reaf->pFather;
            }
            if (ce > max) {
                max = ce;
            }
        }
        t = t->pRight;
    }
    return max;
}
int max_ce = 0;

void Look2(struct treeNode *root) {
    if (NULL == root) {
        return;
    }
    Look2(root->pLeft); // 左子树入栈
    if (NULL  == root->pLeft && NULL == root->pRight) {
        int cen = 0;
        struct treeNode *reaf = root;
        while(reaf != NULL) {
            cen++;
            reaf = reaf->pFather;
        }
        if (cen > max_ce) {
            max_ce = cen;
        }
    }
    Look2(root->pRight); // 右子树入栈
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));
    Look2(&t1);
    printf("叶子反根递归:%d\n", max_ce);
    printf("叶子反根非递归:%d\n", Look(&t1));


    return 0;
}

最大栈法-数组

  • 可以根据之前的前中后序遍历的过程，发现栈内的元素根层数是有关系的，后序遍历是最大的栈内元素
//
// Created by Cauchyshy on 2023/5/25.
//
#include <iostream>
#include <cstdio>
#include <malloc.h>

using namespace std;
#define TREE_DEEP 15

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

// 数组栈
// 由于不需要前后指针 直接用树叶指针类型即可 装树几点地址即可
struct treeNode *stack[TREE_DEEP] = {0};

// 用下标最栈顶指示符即可 栈顶
int stacktop = -1; // -1表示空栈 因为下标从0开始 0元素就是一个栈内元素了

// 入栈
void push(struct treeNode *node) {
    if (NULL == node)
        return ;
    stacktop++; // 栈顶标记先自加1
    stack[stacktop] = node; // 然后对栈顶赋值
}

//出栈
struct treeNode * pop(void) {
    if (stacktop == -1)
        return NULL;
    int pre = stacktop;
    stacktop--;
    return stack[pre];
}

/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

int maxCe;
void Look2(struct treeNode *root) {
    if (NULL == root) {
        return ;
    }
    struct treeNode *pre = NULL;
    while (1) {
        // 左子树入栈
        while (root != NULL) {
            push(root);
            root = root->pLeft;
        }
		// 这里判断栈内元素最大个数
        if (maxCe < stacktop) {
            maxCe = stacktop;
        }

        if (-1 == stacktop)
            break;
        if (NULL == stack[stacktop]->pRight || stack[stacktop]->pRight == pre) {
            pre = pop();
            // printf("%d")
        } else {
            root = stack[stacktop]->pRight;
        }
    }
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));
    Look2(&t1);
    printf("最大栈法-数组:%d\n", maxCe + 1);



    return 0;
}

最大栈法-链表栈

//
// Created by Cauchyshy on 2023/5/25.
//
#include <iostream>
#include <cstdio>
#include <malloc.h>

using namespace std;

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

// 链表结构的栈 尾添加尾删除 双向带空头链表
// 栈节点
struct stack {
    struct treeNode *node; // 指向树的节点
    struct stack *pre; // 指向前一个节点
    struct stack *next; // 指向下一个节点
};
struct stack head; // 空头
struct stack *stacktop = &head; // 栈顶指针

// 入栈 链表尾添加
void push(struct treeNode *node) {
    // 申请节点 并且成员赋值
    struct stack *temp = (struct stack *)malloc(sizeof(struct stack));
    if (NULL == temp) {
        return ;
    }
    // 赋初值
    temp->pre = NULL;
    temp->next = NULL;
    temp->node = node;
    // 尾巴连接
    stacktop->next = temp;
    temp->pre = stacktop;
    // 栈顶指针后移
    stacktop = stacktop->next;
}

// 出栈 双向链表尾删除
struct treeNode *pop(void) {
    if (stacktop == &head) {
        // 栈空
        return NULL;
    }
    struct treeNode *temp = stacktop->node; // 得到栈顶的树节点

    stacktop = stacktop->pre; // 节点前移
    free(stacktop->next); // 释放节点
    stacktop->next = NULL; // 新尾指针指向空
    return temp;
}



/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

int getMaxNode() {
    int ans = 0;
    // 因为是空头 下一个就是数据了 如果没有就是0
    if (head.next == NULL)
        return 0;
    struct stack *tp = head.next;
    while(tp != NULL) {
        ans++;
        tp = tp->next;
    }
    return ans;
};

int maxCe;
void Look2(struct treeNode *root) {
    if (NULL == root) {
        return ;
    }
    struct treeNode *pre = NULL;
    while (1) {
        // 左子树入栈
        while (root != NULL) {
            push(root);
            root = root->pLeft;
        }

//        if (maxCe < stacktop) {
//            maxCe = stacktop;
//        }

        if (&head == stacktop)
            break;

        // 统计栈内元素个数
        if (maxCe < getMaxNode()) {
            maxCe = getMaxNode();
        }

        if (NULL == stacktop->node->pRight || stacktop->node->pRight == pre) {
            pre = pop();
            // printf("%d")
        } else {
            root = stacktop->node->pRight;
        }
    }
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));
    Look2(&t1);
    printf("最大栈法-链表栈:%d\n", maxCe); // 这个不用加一 刚才数组记录的下标 所以要+1
    return 0;
}

进出栈统计法

  • 直接在后序遍历里加减
//
// Created by Cauchyshy on 2023/5/25.
//
#include <iostream>
#include <cstdio>
#include <malloc.h>

using namespace std;
int cnt = 0;

struct treeNode {
    int a; // 数据成员
    struct treeNode *pFather; // 父节点
    struct treeNode *pLeft; // 左孩子
    struct treeNode *pRight; // 右孩子
};

// 链表结构的栈 尾添加尾删除 双向带空头链表
// 栈节点
struct stack {
    struct treeNode *node; // 指向树的节点
    struct stack *pre; // 指向前一个节点
    struct stack *next; // 指向下一个节点
};
struct stack head; // 空头
struct stack *stacktop = &head; // 栈顶指针

// 入栈 链表尾添加
void push(struct treeNode *node) {
    // 申请节点 并且成员赋值
    struct stack *temp = (struct stack *)malloc(sizeof(struct stack));
    if (NULL == temp) {
        return ;
    }
    cnt++;
    // 赋初值
    temp->pre = NULL;
    temp->next = NULL;
    temp->node = node;
    // 尾巴连接
    stacktop->next = temp;
    temp->pre = stacktop;
    // 栈顶指针后移
    stacktop = stacktop->next;
}

// 出栈 双向链表尾删除
struct treeNode *pop(void) {
    if (stacktop == &head) {
        // 栈空
        return NULL;
    }
    cnt--;
    struct treeNode *temp = stacktop->node; // 得到栈顶的树节点

    stacktop = stacktop->pre; // 节点前移
    free(stacktop->next); // 释放节点
    stacktop->next = NULL; // 新尾指针指向空
    return temp;
}



/**
 * 得到一棵树有多少层
 * 二叉树的高度
 *递归思想 每一个分支都走到叶子节点 看看此时左右子树谁的层更深
 * */

int count(struct treeNode *root) {
    if (NULL == root) {
        return 0; // 树为空
    }
    int left = count(root->pLeft);
    int right = count(root->pRight);
    if (left > right) return left + 1;
    else return right + 1;
}

int getMaxNode() {
    int ans = 0;
    // 因为是空头 下一个就是数据了 如果没有就是0
    if (head.next == NULL)
        return 0;
    struct stack *tp = head.next;
    while(tp != NULL) {
        ans++;
        tp = tp->next;
    }
    return ans;
};

// 直接在后序遍历里面加减
int maxCe = 0;
void Look2(struct treeNode *root) {
    if (NULL == root) {
        return ;
    }
    struct treeNode *pre = NULL;
    while (1) {
        // 左子树入栈
        while (root != NULL) {
            push(root);
            root = root->pLeft;
        }

//        if (maxCe < stacktop) {
//            maxCe = stacktop;
//        }

        if (&head == stacktop)
            break;

        // 统计栈内元素个数
        if (maxCe < cnt) {
            maxCe = cnt;
        }

        if (NULL == stacktop->node->pRight || stacktop->node->pRight == pre) {
            pre = pop();
            // printf("%d")
        } else {
            root = stacktop->node->pRight;
        }
    }
}

int main() {
    struct treeNode t1 = { 1 };
    struct treeNode t2 = { 2 };
    struct treeNode t3 = { 3 };
    struct treeNode t4 = { 4 };
    struct treeNode t5 = { 5 };
    struct treeNode t6 = { 6 };
    struct treeNode t7 = { 7 };
    struct treeNode t8 = { 8 };
    struct treeNode t9 = { 9 };
    struct treeNode t10 = { 10 };

    // 链接
    t1.pLeft = &t2;
    t1.pRight = &t3;
    t1.pFather = NULL;

    t2.pLeft = &t4;
    t2.pRight = &t5;
    t2.pFather = &t1;

    t3.pRight = &t6;
    t3.pLeft = NULL;
    t3.pFather = &t1;

    t4.pLeft = NULL;
    t4.pRight = NULL;
    t4.pFather = &t2;

    t5.pLeft = &t7;
    t5.pRight = &t8;
    t5.pFather = &t2;

    t6.pLeft = &t9;
    t6.pRight = &t10;
    t6.pFather = &t3;

    t7.pLeft = NULL;
    t7.pRight = NULL;
    t7.pFather = &t5;

    t8.pLeft = NULL;
    t8.pRight = NULL;
    t8.pFather = &t5;

    t9.pLeft = NULL;
    t9.pRight = NULL;
    t9.pFather = &t6;

    t10.pLeft = NULL;
    t10.pRight = NULL;
    t10.pFather = &t6;
    printf("%d\n", count(&t1));
    Look2(&t1);
    printf("进出栈统计法:%d\n", maxCe); // 这个不用加一 刚才数组记录的下标 所以要+1



    return 0;
}
求二叉树高度
12-14
二叉树高度 二叉树高度 二叉树高度 二叉树高度 二叉树高度
C++ 实现：计算二叉树深度的递归方法
12-26
通过这一示例，读者可以深入理解递归算法的应用，掌握二叉树深度的计算方法，并为其他树形结构的相关编程打下基础。这不仅提升了编程能力，也为学习更复杂的数据结构奠定了良好的基础。希望该示例能激励更多的编程...
求二叉树的高度
L_Aster的专栏
05-27 589
一、递归实现int Max(int a,int b)//a,b中的最大值 { return a>b?a:b; } int GetHeight(struct BTree *T) { if(!T) return 0;//递归出口 return Max(GetHeight(T->left),GetHeight(T->right))+1;//递归求出左子树和右子树的高度 }
二叉树之树的高以及遍历
最新发布
weixin_73012949的博客
03-23 95
从根节点到叶节点的最长路径中的边数就是二叉树的高。
二叉树求高度
swineherd的博客
08-24 329
#include&lt;bits/stdc++.h&gt; using namespace std; typedef char ElementType; typedef struct TNode *Position; typedef Position BinTree; struct TNode{     ElementType Data;     BinTree Left;     BinTre...
Java实现二叉树的建立、计算高度与递归输出操作示例
08-26
Java实现二叉树的建立、计算高度与递归输出操作示例 本文将详细介绍Java实现二叉树的建立、计算高度与递归输出操作，涵盖了Java二叉树的创建、遍历、计算等相关算法实现技巧。 一、Java实现二叉树的建立 在Java中...
二叉树高度计算
05-31
计算二叉树的高度可以使用递归的方法。先判断二叉树是否为空，为空则高度为0。如果不为空，则递归计算左子树和右子树的高度，然后取左右子树高度的最大值并加1（加1是因为要算上根节点），即为整个二叉树的高度。 ...
二叉树高度计算与树型结构解析
"二叉树高度计算、树的定义与基本术语、二叉树的定义、性质和存储结构、哈夫曼树" 在计算机科学中，树是一种非线性数据结构，它由n（n>=0）个有限数据元素构成，这些元素之间存在一种特定的关系，使得它们形成层次...
二叉树高度计算：BTNodeDepth(*b)解析
"二叉树的高度计算方法以及树的基本概念" 在计算机科学中，树是一种非线性数据结构，常用于模拟具有层次关系的问题。在本摘要中，我们将重点讨论二叉树的高度计算以及树的一些基本概念。 首先，让我们深入理解标题...
二叉链表作存储结构，设计求二叉树高度的算法
02-17
以二叉链表作存储结构，设计求二叉树高度的算法。
数据结构——求二叉树高度
NCC__dapeng的博客
11-07 8204
这个题。。。有点迷。。。 首先注意题干，人家让你写的是Getheight函数，那个构建树那个函数 是被忽略掉不需要去写的，一开始还在为怎么去构建这个树想了半天。。。。 裁判测试程序样例： #include &lt;stdio.h&gt; #include &lt;stdlib.h&gt; typedef char ElementType; typedef struct TNode *Po...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

只微

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值