【深度学习原理与Pytorch实战笔记-第三章 单车预测器——你的第一个神经网络】

系列文章目录

提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
第1章 深度学习简介
第2章　PyTorch简介
第3章　单车预测器——你的第一个神经网络

---

第三章做的笔记和思考，学pytorch前需要把Python的三大库好好掌握一下

---

3.1 共享单车的烦恼

如何解决共享单车分布不均匀的问题呢？目前的方式是，共享单车公司会雇一些工人来搬运单车，把它们运送到需要单车的区域。但问题是应该运多少单车？什么时候运？运到什么地方呢？这就需要准确地知道共享单车在整个城市不同地点的数量分布情况，而且需要提前做出安排，因为工人运送单车还有一定的延迟性。这对于共享单车公司来说是一个非常严峻的挑战。

为了更加科学有效地解决这个问题，我们需要构造一个共享单车预测器，用来预测某一时间、某一停放区域的单车数量，供共享单车公司参考，以实现对单车的合理投放。

要构建这样的预测器，就需要一定的共享单车数据。为了避免商业纠纷，也为了让本书的开发和讲解更方便，本例将会使用国外的一个共享单车公开数据集(Capital Bikeshare)来完成任务，数据集可从该网址 该网站下载。

下载数据集之后，点击hour.csv打开如下图所示：

该数据是从2011年1月1日到2012年12月31日之间某地的单车使用情况，每一行都代表一条数据记录，共17379条。一条数据记录了一个小时内某地的星期几、是否是假期、天气和风速等情况，以及该地区的单车使用量（用cnt变量表示），它是我们最关心的量。

我们可以截取一段时间的数据，将cnt随时间的变化关系绘制成图。图3.2是2011年1月1日到2011年1月10日的数据，横坐标是时间，纵坐标是单车的数量。单车数量随时间波动，并且呈现出一定的规律性。不难看出，工作日的单车数量高峰远高于周末的。

我们要解决的问题就是，能否根据历史数据预测接下来一段时间该地区单车数量的走势呢？在本章中，我们将学习如何设计神经网络模型来预测单车数量。对于这一问题，我们并不是一下子提供一套完美的解决方案，而是通过循序渐进的方式，尝试不同的解决方案。结合这一问题，我们将主要讲解什么是人工神经元、什么是神经网络、如何根据需要搭建一个神经网络，以及什么是过拟合、如何解决过拟合问题，等等。除此之外，我们还将学习如何对一个神经网络进行剖析，从而理解其工作原理以及与数据的对应。

3.2 单车预测器1.0

本节将构建一个单车预测器，它是一个单一隐含单元的神经网络。我们将训练它拟合共享单车的波动曲线。不过，在设计单车预测器之前，我们有必要了解一下人工神经网络的概念和工作原理。

3.2.1 人工神经网络简介

人工神经网络是一种受人脑的生物神经网络启发而设计的计算模型，非常擅长从输入的数据和标签中学习映射关系，从而完成预测或者分类问题。人工神经网络也称通用拟合器，因为它可以拟合任意的函数或映射。

前馈神经网络是最常用的一种网络，它一般包括3层人工神经元 ，即输入层、隐含层和输出层， 如图3.3所示。其中，隐含层可以包含多层，这就构成了所谓的深度神经网络。

图3.3中的每一个圆圈代表一个人工神经元，连线代表人工突触，它将两个神经元联系了起来。每条连边上都包含一个数值，叫作权重，通常用w来表示。

神经网络的运行通常包含前馈的预测过程（或称为决策过程）和反馈的学习过程。

在前馈的预测过程中，信号从输入单元输入，并沿着网络连边传输，每个信号会与连边上的权重进行乘积，从而得到隐含单元的输入；接下来，隐含单元对所有连边输入的信号进行汇总（求和），然后经过一定的处理（具体处理过程将在下一节讲述）后输出；这些输出的信号再乘以从隐含层到输出的那组连线上的权重，从而得到输入给输出单元的信号；最后，输出单元对每一条输入连边的信号进行汇总，加工处理后输出。最后的输出就是整个神经网络的输出。神经网络在训练阶段将会调节每条连边上的权重w的数值。

在反馈的学习过程中，每个输出神经元会首先计算出它的预测误差，然后将这个误差沿着网络的所有连边进行反向传播，得到每个隐含层节点的误差，最后根据每条连边所连通的两个节点的误差计算连边上的权重更新量，从而完成网络的学习与调整。

下面，我们就从人工神经元开始详细讲述神经网络的工作过程。

3.2.2 人工神经元

人工神经网络类似于生物神经网络，由人工神经元（简称神经元）构成。神经元用简单的数学模型来模拟生物神经细胞的信号传递与激活。为了理解人工神经网络的运作原理，我们先来看一个最简单的情形：单神经元模型。如图3.4所示，它只有一个输入单元、一个隐含单元和一个输出单元。

x表示输入的数据，y表示输出的数据，它们都是实数。从输入单元到隐含层的权重w、隐含单元偏置b、隐含层到输出层的权重w`都是可以任意取值的实数。

由此可见，当w>0的时候，它的大小控制着函数的弯曲程度，w越大，它在0点附近就越弯曲，因此从x=0的突变也就越剧烈；当w<0的时候，曲线发生了左右翻转，它会从1突变到0。

再来看看参数b对曲线的影响。保持w=w`=1不变，如图3.7所示。

可以清晰地看到，b控制着sigmoid函数曲线的水平位置。b>0，函数图像往左平移；反之往右平移。最后，我们看看w`如何影响该曲线，如图3.8所示。

不难看出，当w`>0的时候， w `控制着曲线的高矮；当 w `<0的时候，曲线的方向发生上下颠倒。

可见，通过控制w、w`和b这3个参数，我们可以任意调节从输入x到输出y的函数形状。但是，无论如何调节，这条曲线永远都是S形（包括倒S形）的。要想得到更加复杂的函数图像，我们需要引入更多的神经元。

3.2.3 两个隐含神经元

下面我们把模型做得更复杂一些，看看两个隐含神经元会对曲线有什么影响，如图3.9所示。

输入信号进入网络之后会兵分两路，一路从左侧进入第一个神经元，另一路从右侧进入第二个神经元。这两个神经元分别完成计算后，通过w1`和w2`进行加权求和得到y。所以，输出y]实际上就是两个神经元的叠加。这个网络仍然是一个将x映射到y的函数，函数方程为：
$$y={\omega }_1^{\prime }\sigma ({\omega }_{1}x+b_1)+{\omega }_2^{\prime }\sigma ({\omega }_{2}x+b_2)$$

由此可见，合成的函数图像变为了一条具有两个阶梯的曲线。

由此可见，我们合成了一条具有单一波峰的曲线，有点儿类似于正态分布的钟形曲线。一般地，只要变换参数组合，我们就可以用两个隐含神经元拟合出任意具有单峰的曲线。

那么，如果有4个或者6个甚至更多的隐含神经元，不难想象，就可以得到具有双峰、三峰和任意多个峰的曲线，我们可以粗略地认为两个神经元可以用来逼近一个波峰（波谷）。事实上，对于更一般的情形，科学家早已从理论上证明，用有限多的隐含神经元可以逼近任意的有限区间内的曲线，这叫作通用逼近定理(universal approximation theorem)。

3.2.4 训练与运行

在前面的讨论中，我们看到，只要能够调节神经网络中各个参数的组合，就能得到想要的任何曲线。可问题是，我们应该如何选取这些参数呢？答案就在于训练。

在前面的讨论中，我们看到，只要能够调节神经网络中各个参数的组合，就能得到想要的任何曲线。可问题是，我们应该如何选取这些参数呢？答案就在于训练。要想完成神经网络的训练，首先要给这个神经网络定义一个损失函数，用来衡量网络在现有的参数组合下输出的表现。这就类似于第2章中利用线性回归预测房价中的总误差函数（即拟合直线与所有点距离的平方和）L。同样，在单车预测的例子中，我们也可以将损失函数定义为对于所有的数据样本，神经网络预测的单车数量与实际数据中单车数量之差的平方和的均值，即：
$$L=\frac{1}{N}\sum _{i=1}^N({\stackrel{‘}{y}}_i-y_i{)}^2$$
`

这里，N为样本总量，yi`为神经网络计算得来的预测单车数量，yi为实际数据中该时刻该地区的单车数量。

有了这个损失函数L，我们就有了调整神经网络参数的方向——尽可能地让L最小化。因此，神经网络要学习的就是神经元之间连边上的权重及偏置，学习的目的是得到一组能够使总误差最小的参数值组合。

这是一个求极值的优化问题，高等数学告诉我们，只需要令导数为零就可以求得。然而，由于神经网络一般非常复杂，包含大量非线性运算，直接用数学求导数的方法行不通，**所以，我们一般使用数值的方式来进行求解，也就是梯度下降算法。**每次迭代都向梯度的负方向前进，使得误差值逐步减小。参数的更新要用到反向传播算法，将损失函数[L沿着网络一层一层地反向传播，来修正每一层的参数。我们在这里不会详细介绍反向传播算法，因为PyTorch已经自动将这个复杂的算法变成了一个简单的命令：backward。只要调用该命令，PyTorch就会自动执行反向传播算法，计算出每一个参数的梯度，我们只需要根据这些梯度更新参数，就可以完成学习。

神经网络的学习和运行通常是交替进行的。也就是说，**在每一个周期，神经网络都会进行前馈运算，从输入端运算到输出端；然后，根据输出端的损失值来执行反向传播算法，从而调整神经网络上的各个参数。**不停地重复这两个步骤，就可以令神经网络学习得越来越好。

3.2.5 失败的神经预测器

在弄清楚了神经网络的工作原理之后，下面我们来看看如何用神经网络预测共享单车使用量。我们希望仿照预测房价的做法，利用人工神经网络来拟合一个时间段内的单车曲线，并给出在未来时间点单车使用量的曲线。

为了让演示更加简单清晰，我们仅选择了数据中的前50条记录，绘制成如图3.12所示的曲线。在这条曲线中，横坐标是数据记录的编号，纵坐标是对应的单车数量。

接下来，我们就要设计一个神经网络，它的输入x就是数据编号，输出则是对应的单车数量。通过观察这条曲线，我们发现它至少有3个峰，采用10个隐含单元就足以拟合这条曲线了。因此，我们的人工神经网络架构如图3.13所示。

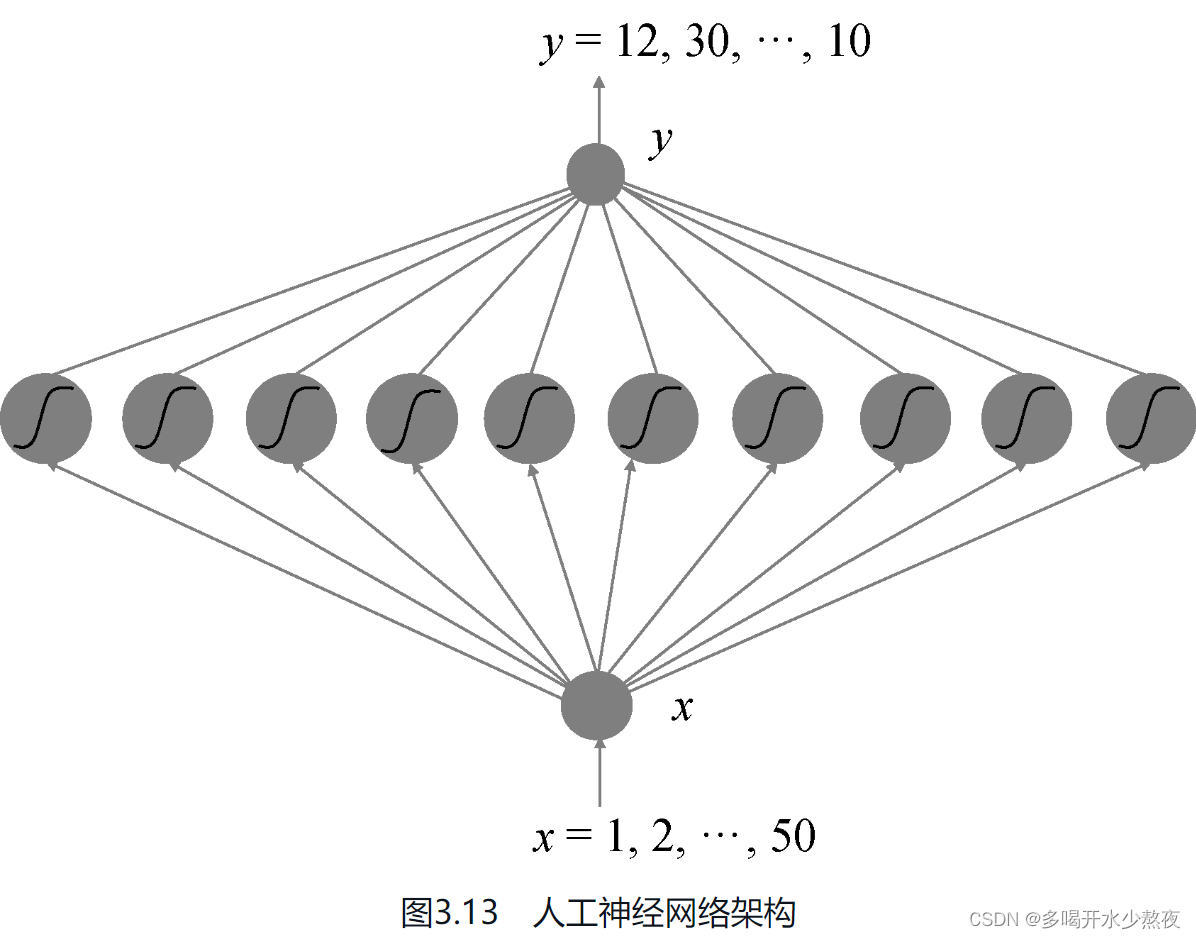
接下来，我们动手编写程序实现这个网络。首先导入该程序所使用的所有依赖库。这里我们使用pandas库来读取和操作数据。读者需要先安装这个程序包，在Anaconda环境下运行conda install pandas即可：

所有代码如下：

import numpy as np
import pandas as pd
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
#导入数据
data_path='D:\deepLearning\hour.csv'
#rides为一个dataframe对象
rides=pd.read_csv(data_path)
rides.head()#输出部分数据
counts = rides['cnt'][:50]#截取前50数据
x = np.arange(len(counts))
y=np.array(counts)#单车数量
plt.figure(figsize=(10,7))
plt.plot(x,y,'o-')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
#在这里，我们使用了pandas库，从CSV文件中快速导入数据到rides里面。
# rides可以按照二维表的形式存储数据，并可以像访问数组一样对其进行访问和操作。
# rides.head()的作用是打印输出部分数据记录
#之后，我们从rides的所有记录中选出前50条，并只筛选出cnt字段放入counts数组中。
# 这个数组就存储了前50条单车使用数量记录。接着，我们绘制前50条记录的图，如图3.13所示。
#准备好了数据，我们就可以用PyTorch来搭建人工神经网络了。
# 与第2章的线性回归例子类似，我们首先需要定义一系列的变量，包括所有连边的权重和偏置，并通过这些变量的运算让PyTorch自动生成计算图：

#输入变量，1，2，3...这样的一维数组
x=torch.FloatTensor(np.arange(len(counts),dtype=float))
#输出变量，他是从数据counts中读取的每一时刻的单车数，共50个数据点的一维数组，作为标准答案
y=torch.FloatTensor(np.array(counts,dtype=float))
sz=10#设置隐含神经元的数量
#初始化输入层到隐含层的权重矩阵，它的尺寸是（1，10）
weights = torch.randn((1,sz),requires_grad=True)
#初始化隐含层节点的偏置向量，它是尺寸为10的一维向量
biases = torch.randn((sz),requires_grad=True)
#初始化从隐含层到输出层的权重矩阵，它的尺寸是（10，1）
weights2 = torch.randn((sz,1),requires_grad=True)
#设置好变量和神经网络的初始参数，接下来迭代地训练这个神经网络：
learning_rate=0.001#设置学习率
losses=[]#记录每一次迭代的损失函数值，以方便以后绘图
x=x.view(50,-1)
y=y.view(50,-1)
for i in range(100000):
    #从输入层到隐含层的计算
    hidden = x * weights + biases
    #此时 hidden变量的尺寸是（50，10）即50个数据点，10个隐含神经元
    #将sigmoid函数应用在隐含层的每一个神经元上
    hidden = torch.sigmoid(hidden)
    #隐含层输出到输出层，计算得到最终预测值
    predictions = hidden.mm(weights2)
    #此时，predictions的尺寸为（50，1），即50个数据点的预测值
    #通过与数据中的标准答案y进行比较，计算均方误差
    loss = torch.mean((predictions-y) ** 2)
    #此时，loss为一个标量，即一个数
    losses.append(loss.data.numpy())

    if i % 10000 == 0:#每隔10000个周期打印一次损失函数数值
        print('loss',loss)

    # 接下来执行梯度下降算法，将误差反向传播
    loss.backward()#对损失函数进行梯度反转
    #利用上一步计算中得到的weights、biases等梯度信息更新weights和biases的数值
    weights.data.add_(-learning_rate * weights.grad.data)
    biases.data.add_(-learning_rate * biases.grad.data)
    weights2.data.add_(-learning_rate * weights2.grad.data)

    #清空所有变量的梯度值
    weights.grad.data.zero_()
    biases.grad.data.zero_()
    weights2.grad.data.zero_()

#在上面这段代码中，我们进行了100000步训练迭代。
# 在每一次迭代中，我们都将50个数据点的x作为数组全部输入神经网络，
# 并让神经网络按照从输入层到隐含层、再从隐含层到输出层的步骤，一步步完成计算，最终输出对50个数据点的预测数组prediction。
#之后，计算prediction和标准答案y之间的误差，并计算出50个数据点的平均误差loss，
# 这就是我们前面提到的损失函数L。接着，调用loss.backward()完成误差沿着神经网络的反向传播过程，
# 从而计算出计算图上每一个叶节点的梯度更新数值，并记录在每个变量的.grad属性中。最后，我们用这个梯度数值来更新每个参数的数值，从而完成了一步迭代。
#仔细对比这段代码和第2章中的线性回归代码就会发现，除了中间的运算过程和损失函数有所不同外，其他的操作全部相同。
# 事实上，在本书中，几乎所有的机器学习案例都采用了这样的步骤，即前馈运算、反向传播计算梯度、根据梯度更新参数值。

#我们可以打印出Loss随着一步步迭代下降的曲线，这可以帮助我们直观地看到神经网络训练的过程，如图3.14所示。

plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.show()

书上得到的结果图：

我得到的结果图在一些位置有密集的波动，不知道是哪里有问题：

由该曲线可以看出，随着时间的推移，神经网络预测的误差的确在一步步减小。而且，大约到20000步后，误差基本就不会出现明显的下降了。

调试了一下，如果神经元数比较少则会在后面出现抖动下降，神经元设置成20的结果和10个的结果基本相同

后面的图又变了：

接下来，我们可以把训练好的网络对这50个数据点的预测曲线绘制出来，并与标准答案y进行对比，代码如下：

x_data = x.data.numpy() #获得x包裹的数据
plt.figure(figsize=(10,7))
xplot, = plt.plot(x_data,y.data.numpy(),'o')
yplot, = plt.plot(x_data,predictions.data.numpy())
plt.xlabel('X')
plt.ylabel('Y')
plt.legend([xplot,yplot],['Data','Prediction under 1000000 epochs '])
plt.show()

最后的可视化图像如图3.15所示。

               图3.15　模型拟合训练数据的可视化

可以看到，我们的预测曲线在第一个波峰比较好地拟合了数据，但是在此后，它却与真实数据相差甚远。这是为什么呢？

我们知道，x的取值范围是1~50，而所有权重和偏置的初始值都是设定在(-1, 1)的正态分布随机数，那么输入层到隐含层节点的数值范围就成了的-50~50，要想将sigmoid函数的多个峰值调节到我们期望的位置，需要耗费很多计算时间。事实上，如果让训练时间更长些，我们可以将曲线后面的部分拟合得很好。

这个问题的解决方法是将输入数据的范围做归一化处理，也就是让x的输入数值范围为0~1。因为数据中x的范围是1~ 50，所以，我们只需要将每一个数值都除以50就可以了：

x=torch.FloatTensor(np.arange(len(counts),dtype=float))/len(counts)

该操作会使[插图]的取值范围变为0.02, 0.04, …, 1。做了这些改进后再来运行程序，可以看到这次训练速度明显加快，拟合效果也更好了，如图3.16所示。

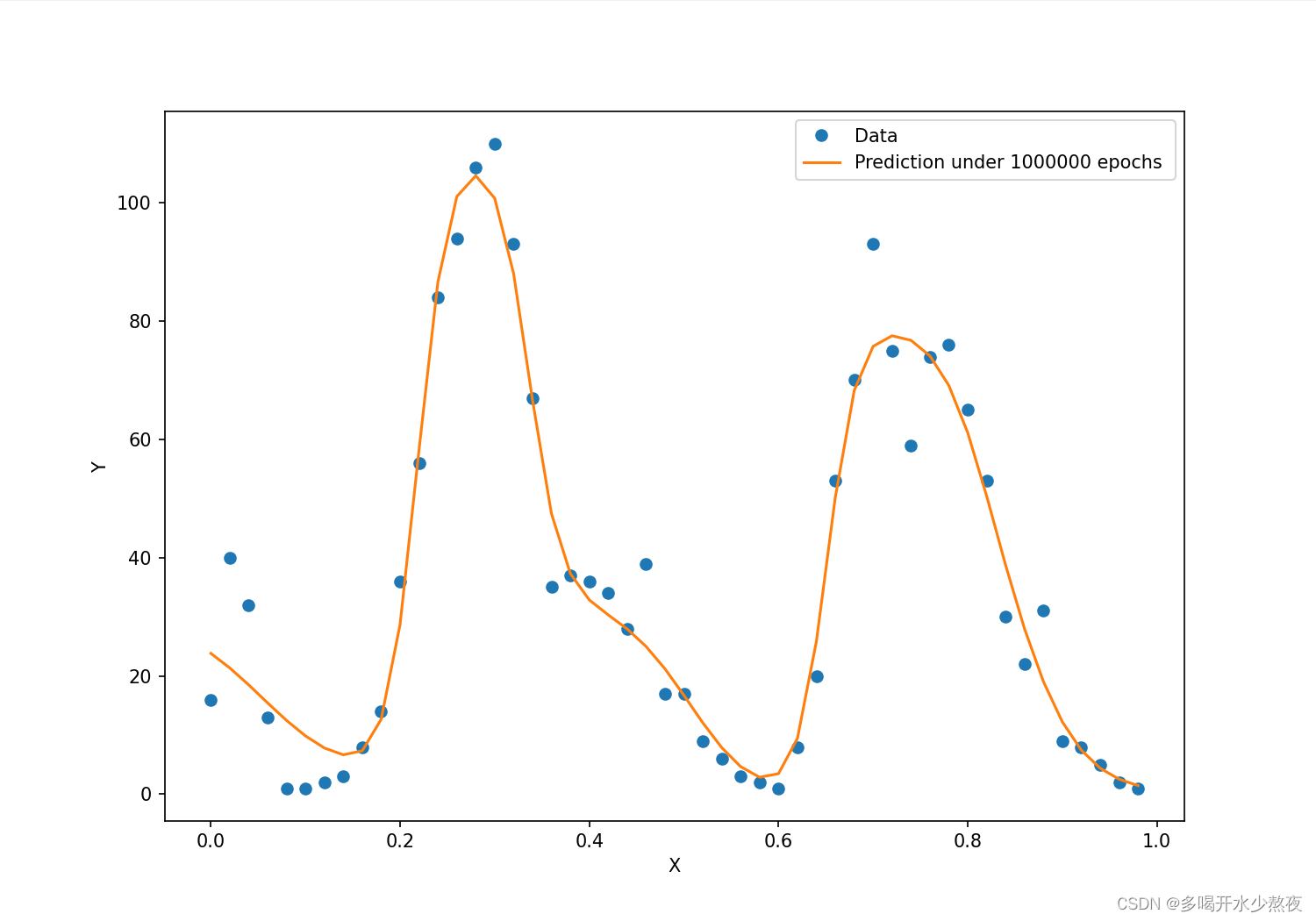
               图3.16　改进的模型拟合训练数据的可视化

我们看到，改进后的模型出现了两个波峰，也非常好地拟合了这些数据点，形成一条优美的曲线。

接下来，我们就需要用训练好的模型来做预测了。我们的预测任务是后面50条数据的单车数量。此时x取值是51, 52, …, 100，同样也要除以50：

counts_predict = rides['cnt'][50:100] #读取待预测的后面50个数据点
x = torch.FloatTensor((np.arange(len(counts_predict),dtype=float)+len(counts))/len(counts))
#读取后面50个点的y数值，不需要做归一化
y = torch.FloatTensor(np.array(counts_predict,dtype=float))
#用x预测y
hidden = x.expand(sz,len(x)).t() *weights.expand(len(x),sz)#从输入层到隐含层的计算
hidden = torch.sigmoid(hidden)#将sigmoid函数应用在隐含层的每一个神经元上
predictions = hidden.mm(weights2)#从隐含层到输出层，计算得到最终预测值
loss = torch.mean((predictions-y) ** 2)#计算预测数据上的损失函数
print(loss)

#将预测曲线绘制出来
x_data = x.data.numpy()
plt.figure(figsize=(10,7))
xplot, = plt.plot(x_data,y.data.numpy(),'o')
yplot, = plt.plot(x_data,predictions.data.numpy())
plt.xlabel('X')
plt.ylabel('Y')
plt.legend([xplot,yplot],['Data','Prediction'])
plt.show()

最终，我们得到了如图3.17所示的曲线，直线是我们的模型给出的预测曲线，圆点是实际数据所对应的曲线。模型预测与实际数据竟然完全对不上！

            图3.17　模型在测试数据上预测失败的曲线

为什么我们的神经网络可以非常好地拟合已知的50个数据点，却完全不能预测出更多的数据点呢？原因就在于——过拟合。

3.2.6 过拟合

所谓过拟合(overfitting)现象，是指模型可以在训练数据上进行非常好的预测，但在全新的测试数据上表现不佳。在这个例子中，训练数据就是前50个数据点，测试数据就是后面50个数据点。我们的模型可以通过调节参数顺利地拟合训练数据的曲线，但是这种刻意适合完全没有推广价值，导致这条拟合曲线与测试数据的标准答案相差甚远。我们的模型并没有学习到数据中的模式。

这是为什么呢？原因就在于我们选择了错误的特征变量：我们尝试用数据的下标(1,2, 3, …)或者它的归一化(0.1, 0.2, …)来对[插图]进行预测。然而曲线的波动模式（也就是单车的使用数量）显然并不依赖于下标，而是依赖于诸如天气、风速、星期几和是否是节假日等因素。然而，我们不管三七二十一，硬要用强大的人工神经网络来拟合整条曲线，这自然就导致了过拟合的现象，而且是非常严重的过拟合。

由这个例子可以看出，一味地追求人工智能技术，而不考虑实际问题的背景，很容易让我们走弯路。当我们面对大数据时，数据背后的意义往往可以指导我们更加快速地找到分析大数据的捷径。

在这一节中，我们虽然费了半天劲也没有真正地解决问题，但是仍然学到了不少知识，包括神经网络的工作原理、如何根据问题的复杂度选择隐含层的数量，以及如何调整数据以加速训练。更重要的是，我们从教训中领教了什么叫作过拟合。

C知道（优快云的gpt回答）
选择隐含层的数量是一个非常重要的问题，因为它会直接影响到神经网络的性能。但是，没有一个通用的规则可以适用于所有的问题。以下是一些可能有用的经验法则和技巧：

经验法则：在输入层和输出层之间，为了计算隐藏层大小我们使用一个一般法则：（输入大小+输出大小）*2/3。这个公式是一个经验法则，可以作为一个起点来选择隐藏层的大小。

基于任务需求：隐藏层的大小应该根据任务的需求来选择。如果任务需要高精度的结果，那么隐藏层的大小应该足够大，以便网络可以学习到更多的特征。如果任务需要快速的结果，那么隐藏层的大小应该足够小，以便网络可以更快地学习。

基于数据集：隐藏层的大小应该根据数据集的大小来选择。如果数据集很小，那么隐藏层的大小应该足够小，以避免过拟合。如果数据集很大，那么隐藏层的大小应该足够大，以便网络可以学习到更多的特征。

基于交叉验证：交叉验证可以帮助我们选择最佳的隐藏层大小。我们可以尝试不同的隐藏层大小，并使用交叉验证来评估每个模型的性能。最终，我们可以选择性能最好的模型。

基于正则化：正则化可以帮助我们选择最佳的隐藏层大小。我们可以尝试不同的正则化参数，并使用交叉验证来评估每个模型的性能。最终，我们可以选择性能最好的模型。

3.3 单车预测器2.0

接下来，就让我们踏上正确解决问题的康庄大道。既然我们猜测利用天气、风速、星期几、是否是节假日等信息可以更好地预测单车使用数量，而且原始数据中包含了这些信息，那么不妨重新设计一个神经网络，把这些相关信息都输入进去，从而预测单车的数量。

3.3.1 数据的预处理过程

然而，在我们动手设计神经网络之前，最好还是再认真了解一下数据，因为增强对数据的了解会起到更重要的作用。

深入观察图3.2中的数据，我们发现，所有的变量可以分成两种：一种是类型变量，另一种是数值变量。

所谓的类型变量，是指这个变量可以在不同的类别中取值，例如星期(week)这个变量就有1, 2, 3, …, 0这几种类型，分别代表星期一、星期二、星期三……星期日这几天。而天气状况(weathersit)这个变量可以从1~4中取值，其中1表示晴天，2表示多云，3表示小雨/雪，4表示大雨/雪。

另一种类型是数值类型，这种变量会从一个数值区间中连续取值。例如，湿度(humidity)就是一个从[0, 1]区间中连续取值的变量。温度、风速也是这种类型的变量。

我们不能将不同类型的变量不加任何处理地输入神经网络，因为不同的数值代表完全不同的含义。在类型变量中，数字的大小实际上没有任何意义。比如数字5比数字1大，但这并不代表周五会比周一更特殊。除此之外，不同的数值类型变量的变化范围也不一样。如果直接把它们混合在一起，势必会造成不必要的麻烦。综合以上考虑，我们需要对两种变量分别进行预处理。

类型变量的独热编码

类型变量的大小没有任何含义，只是为了区分不同的类型而已。比如季节这个变量可以等于1、2、3、4，即四季，数字仅仅是对它们的区分。我们不能将season变量直接输入神经网络，因为season数值并不表示相应的信号强度。我们的解决方案是将类型变量转化为“独热编码”，如表3.1所示。

采用这种编码后，不同的数值就转变为了不同的向量，这些向量的长度都是4，而只有一个位置为1，其他位置都是0。1代表激活，于是独热编码的向量就对应了不同的激活模式。这样的数据更容易被神经网络处理。更一般地，如果一个类型变量有n个不同的取值，那么我们的独热编码所对应的向量长度就为n。

接下来，我们只需要在数据中将某一列类型变量转化为多个列的独热编码向量，就可以完成这种变量的预处理了，如图3.18所示。

因此，原来的weekday这个属性就转变为7个不同的属性，数据库一下就增加了6列。pandas可以很容易实现上面的操作，代码如下：

dummy_fields = ['season','weathersit','mnth','hr','weekday'] #所有类型编码变量的名称
for each in dummy_fields:
    #取出所有类型变量，并将它们转变为独热编码
    dummies = pd.get_dummies(rides[each],prefix=each,drop_first=False)
    #将新的独热编码变量与原有的所有变量合并到一起
    rides = pd.concat([rides,dummies],axis=1)

#将原来的类型变量从数据表中删除
fields_to_drop = ['instant','dteday','season','weathersit','weekday','atemp','mnth','workingday','hr']
data = rides.drop(fields_to_drop,axis=1)#将它们从数据库的变量中删除

报错：libpng warning: iCCP: cHRM chunk does not match sRGB
解决方法：Ctrl+Shift切换掉QQ输入法

数值类型变量的处理

数值类型变量的问题在于每个变量的变化范围都不一样，单位也不一样，因此不同的变量不能进行比较。**我们采取的解决方法是对这种变量进行标准化处理，也就是用变量的均值和标准差来对该变量做标准化，从而把特征数值的平均值变为0，标准差变为1。**比如，对于温度temp这个变量来说，它在整个数据库中取值的平均值为mean(temp)，标准差为std(temp)，那么，归一化的温度计算为：
$$tem{p}^{\prime }=\frac{temp-mean(temp)}{std(temp)}$$
temp`是一个位于[-1, 1]区间的数。这样做的好处是可以将不同取值范围的变量设置为处于平等的地位。

我们可以用以下代码来对这些变量进行标准化处理：

quant_features = ['cnt','temp','hum','windspeed']
scaled_features = {}#将每一个变量的均值和方差都存储到scaled_features变量中
for each in quant_features:
    #计算这些变量的均值和方差
    mean, std = data[each].mean(),data[each].std()
    scaled_features[each] = [mean, std]
    #对每一个变量进行标准化
    data.loc[:,each] = (data[each] - mean)/ std
    

数据集的划分

预处理做完以后，我们的数据集包含了17379条记录、59个变量。接下来，我们将对这个数据集进行划分。

首先，我们将变量集合分为特征和目标两个集合。其中，特征变量集合包括：年份(yr)、是否是节假日(holiday)、温度(temp)、湿度(hum)、风速(windspeed)、季节1_{4(season)、天气1}4（weathersit，不同天气状况）、月份1_{12(mnth)、小时0}23(hr)和星期0~6(weekday)，它们是输入给神经网络的变量。目标变量包括：用户数(cnt)、临时用户数(casual)，以及注册用户数(registered)。其中我们仅仅将cnt作为目标变量，另外两个暂时不做任何处理。我们将利用56个特征变量作为神经网络的输入，来预测1个变量作为神经网络的输出。

接下来，我们将17379条记录划分为两个集合：前16875条记录作为训练集，用来训练我们的神经网络；后21天的数据（504条记录）作为测试集，用来检验模型的预测效果，这部分数据是不参与神经网络训练的，如图3.20所示。

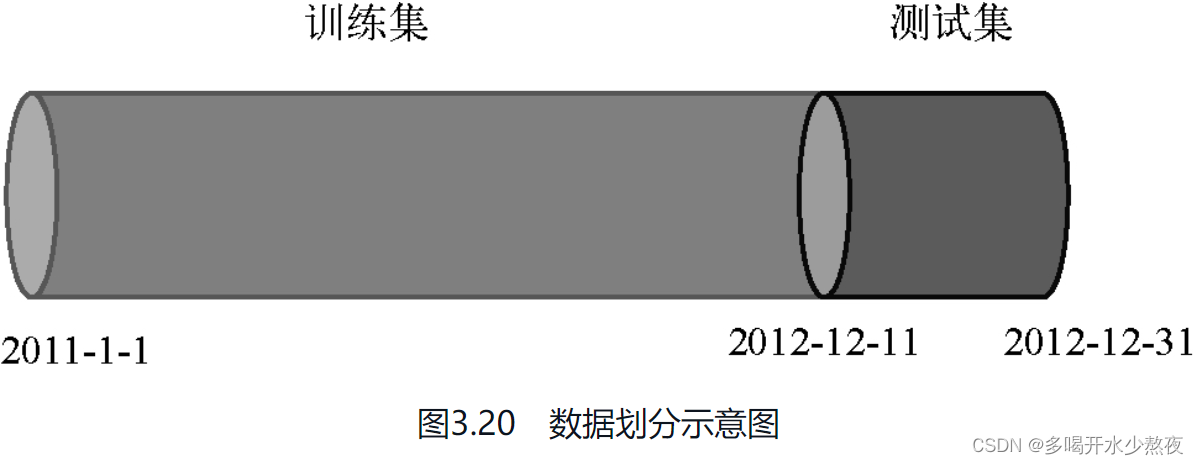
数据处理代码如下：

test_data = data[-21*24:]#选出训练集
train_data = data[:-21*24]#选出测试集
#目标列包含的字段
target_fields = ['cnt','casual','registered']
#将训练集划分成特征变量列和目标特征列
features, targets = train_data.drop(target_fields,axis=1),train_data[target_fields]
#将测试集划分成特征变量列和目标变量列
test_features, test_targets = test_data.drop(target_fields,axis=1),test_data[target_fields]
#将数据类型转换为Numpy数组
X = features.values #将数据从pandas dataframe 转化为Numpy
Y = targets['cnt'].values
Y = Y.astype(float)

Y = np.reshape(Y,[len(Y),1])
losses = []

3.3.2 构建神经网络

在数据处理完毕后，我们将构建新的人工神经网络。这个网络有3层：输入层、隐含层和输出层。每个层的尺寸（神经元个数）分别是56、10和1（如图3.21所示）。其中，输入层和输出层的神经元个数分别由数据决定，隐含神经元个数则根据我们对数据复杂度的预估决定。通常，数据越复杂，数据量越大，需要的神经元就越多。但是神经元过多容易造成过拟合。

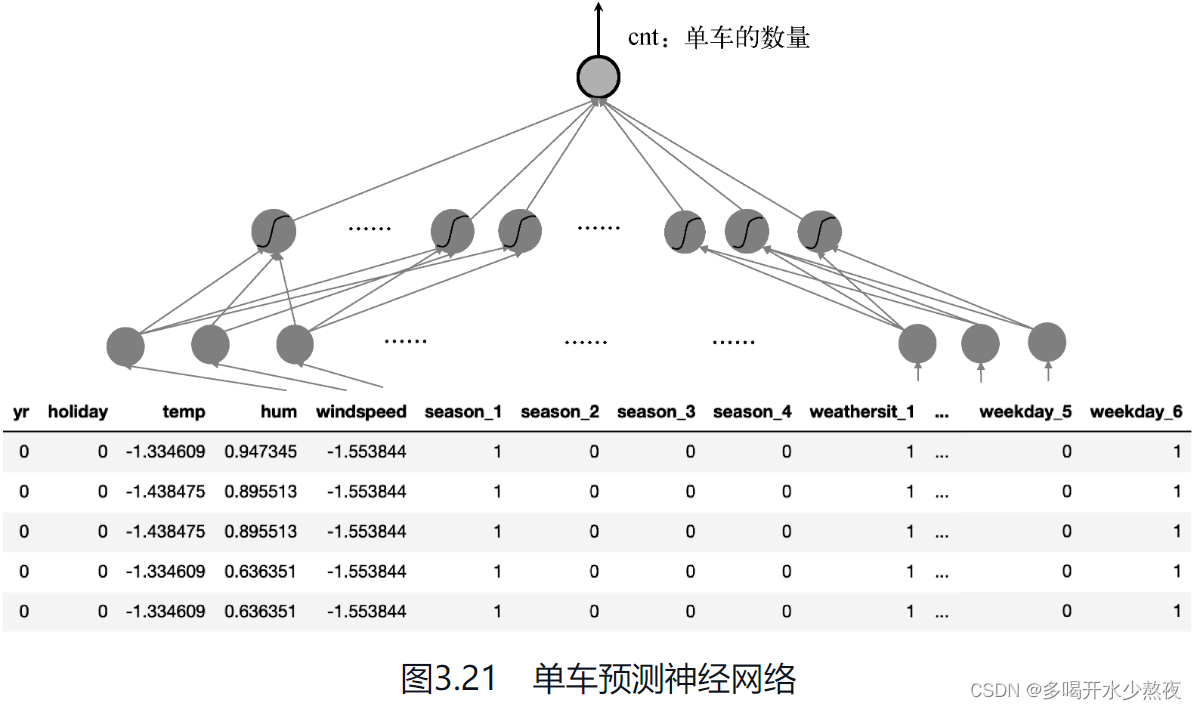
除了前面讲的用手工实现神经网络的张量计算完成神经网络搭建以外，PyTorch还实现了自动调用现成的函数来完成同样的操作，这样的代码更加简洁，如下所示：

#定义神经网络架构，features.shape[1] 个输入单元，10个隐含单元，1个输出单元
input_size = features.shape[1]
hidden_size = 10
output_size = 1
batch_size = 128
neu = torch.nn.Sequential(
    torch.nn.Linear(input_size,hidden_size),
    torch.nn.Sigmoid(),
    torch.nn.Linear(hidden_size,output_size),
)

在这段代码里，我们可以调用torch.nn.Sequential()来构造神经网络，并存放到neu变量中。torch.nn.Sequential()这个函数的作用是将一系列的运算模块按顺序搭建成一个多层的神经网络。在本例中，这些模块包括从输入层到隐含层的线性映射Linear(input_size, hidden_size)、隐含层的非线性sigmoid函数torch.nn.Sigmoid()，以及从隐含层到输出层的线性映射torch.nn.Linear(hidden_size, output_size)。值得注意的是，Sequential里面的层次并不与神经网络的层次严格对应，而是指多步的运算，它与动态计算图的层次相对应。

我们也可以使用PyTorch自带的损失函数：

cost = torch.nn.MSELoss()

这是PyTorch自带的一个封装好的计算均方误差的损失函数，它是一个函数指针，赋予了变量cost。在计算的时候，我们只需要调用cost(x,y)就可以计算预测向量x和目标向量y之间的均方误差。

除此之外，PyTorch还自带了优化器来自动实现优化算法：

optimizer = torch.optim.SGD(neu.parameters(),lr = 0.01)

torch.optim.SGD()调用了PyTorch自带的随机梯度下降算法(stochastic gradient descent，SGD)作为优化器。在初始化optimizer的时候，我们需要待优化的所有参数（在本例中，传入的参数包括神经网络neu包含的所有权重和偏置，即neu.parameters()），以及执行梯度下降算法的学习率lr=0.01。在一切都准备好之后，我们便可以实施训练了。

数据的批处理

然而，在进行训练循环的时候，我们还会遇到一个问题。在前面的例子中，在每一个训练周期，我们都将所有的数据一股脑儿地输入神经网络。这在数据量不大的情况下没有什么问题。但是，现在的数据量是16875条，在这么大的数据量下，如果在每个训练周期都处理所有数据，则会出现运算速度过慢、迭代可能不收敛等问题。

解决方法通常是采取**批处理(batch processing)的模式，也就是将所有的数据记录划分成一个批次大小(batch size)的小数据集，然后在每个训练周期给神经网络输入一批数据，**如图3.22所示。批次的大小依问题的复杂度和数据量的大小而定，在本例中，我们设定batch_size=128。

采用批处理后的训练代码如下：

#神经网络训练循环
losses = []
for i in range(1000):
    #每128个样本点划分为一批，在循环的时候一批一批地读取
    batch_loss = []
    # start 和 end 分别是提取一批数据的起始下标和终止下标
    for start in range(0,len(X),batch_size):
        end = start + batch_size if start + batch_size < len(X) else len(X)
        xx = torch.FloatTensor(X[start:end])
        yy = torch.FloatTensor(Y[start:end])
        predict = neu(xx)
        loss = cost(predict,yy)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        batch_loss.append(loss.data.numpy())

    #每隔100步输出损失值
    if i % 100 ==0:
        losses.append(np.mean(batch_loss))
        print(i,np.mean(batch_loss))

#打印输出损失值
plt.plot(np.arange(len(losses))*100,losses)
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.show()

运行这段程序，我们便可以训练这个神经网络了。图3.23展示的是随着训练周期的增加，损失函数的下降情况。其中，横坐标表示训练周期，纵坐标表示平均误差。可以看到，平均误差随训练周期的增加快速下降。

                  图3.23　单车预测器的训练曲线

3.3.3 测试神经网络

接下来，我们便可以用训练好的神经网络在测试集上进行预测，并且将后21天的预测数据与真实数据画在一起进行比较：

targets = test_targets['cnt'] #毒区测试集的cnt数值
targets = targets.values.reshape([len(targets),1])#将数据转换成合适的张量形式
targets = targets.astype(float) #保证数据为实数

x = torch.FloatTensor(test_features.values)
y = torch.FloatTensor(targets)

#用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()
#将此元组解压缩到变量fig和ax.有fig,如果你想改变人物级别的属性或保存数字作为以后的图像文件是非常有用的(例如用fig.savefig(‘yourfilename.png’) 
#plt.subplots()实际上返回了一个包含两个元素的元组.第一个必须是一个图形对象,另一个应该是一组子图对象.
fig, ax =plt.subplots(figsize=(10,7))

mean, std =scaled_features['cnt']
ax.plot(predict * std + mean, label='Prediction')
ax.plot(targets * std + mean, label='Data')
ax.legend()
ax.set_xlabel('Date-time')
ax.set_ylabel('Counts')
dates = pd.to_datetime(rides.loc[test_data.index]['dteday'])
#apply()的返回值就是func()的返回值，apply()的元素参数是有序的，元素的顺序必须和func()形式参数的顺序一致
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24],rotation=45)
plt.show()#不加上这句会错
#网上查的：
# 用训练好的神经网络在测试集上进行预测
targets = test_targets['cnt'] #读取测试集的cnt数值
targets = targets.values.reshape([len(targets),1]) #将数据转换成合适的tensor形式
targets = targets.astype(float) #保证数据为实数

x = torch.tensor(test_features.values, dtype = torch.float, requires_grad = True)
y = torch.tensor(targets, dtype = torch.float, requires_grad = True)

print(x[:10])
# 用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()

print((predict * std + mean)[:10])
# 将后21天的预测数据与真实数据画在一起并比较
# 横坐标轴是不同的日期，纵坐标轴是预测或者真实数据的值
fig, ax = plt.subplots(figsize = (10, 7))

mean, std = scaled_features['cnt']
ax.plot(predict * std + mean, label='Prediction', linestyle = '--')
ax.plot(targets * std + mean, label='Data', linestyle = '-')
ax.legend()
ax.set_xlabel('Date-time')
ax.set_ylabel('Counts')
# 对横坐标轴进行标注
dates = pd.to_datetime(rides.loc[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24], rotation=45)

plt.show()

备注：torch.FloatTensor(test_features.values) 等价于torch.tensor(test_features.values, dtype = torch.float, requires_grad = True)

实际曲线与预测曲线的对比如图3.24所示。其中，横坐标是不同的日期，纵坐标是预测或真实数据的值，虚线为预测曲线，实线为实际数据。

               图3.24　实际曲线与预测曲线的对比

可以看到，两条曲线基本是吻合的，但是在12月25日前后几天的实际值和预测值偏差较大。为什么这段时间的表现这么差呢？

仔细观察数据，我们发现12月25日正好是圣诞节。对于欧美国家来说，圣诞节就相当于我们的春节，在圣诞节假期前后，人们的出行习惯会与往日有很大的不同。但是，在我们的训练样本中，因为整个数据仅有两年的长度，所以包含圣诞节前后的样本仅有一次，这就导致我们没办法对这一假期的模式进行很好的预测。

3.4 剖析神经网络Neu（代码运行结果和书上图差别有些大，花了几个小时也没查到原因，直接对着书上的图看解释吧）

按理说，目前我们的工作已经全部完成了。但是，我们还希望对人工神经网络的工作原理有更加透彻的了解。因此，我们将对这个训练好的神经网络Neu进行剖析，看看它究竟为什么在一些数据上表现优异，而在另一些数据上表现欠佳。

对于我们来说，神经网络在训练的时候发生了什么完全是黑箱，但是，神经网络连边的权重实际上就在计算机的存储中，我们可以把感兴趣的数据提取出来进行分析。

我们定义了一个函数feature()，用于提取神经网络中存储在连边和节点中的所有参数，代码如下：

def feature(X,net):
    #定义一个函数，用于提取网络的权重信息
    #所有网络参数信息全部存储在Neu的named_parameters集合中
    X = torch.from_numpy(X).type(torch.FloatTensor)
    dic = dict(net.named_parameters())#从这个集合中提取数据
    weights = dic['0.weight' ]# 可以按照“层数.名称”来索引集合中的相应参数值
    biases = dic['0.bias']
    h = torch.sigmoid(X.mm(weights.t()) + biases.expand([len(X), len(biases)]))
    #隐含层计算过程
    return h#输出层的计算

在这段代码中，我们用net.named_parameters()命令提取出神经网络的所有参数，其中包括了每一层的权重和偏置，并且把它们放到Python字典中。接下来就可以通过如上代码来提取数据，例如可以通过dic[‘0.weight’]和dic[‘0.bias’]的方式得到第一层的所有权重和偏置。此外，我们还可以通过遍历参数字典dic获取所有可提取的参数名称。

由于数据量较大，因此我们选取了一部分数据输入神经网络，并提取网络的激活模式。我们知道，预测不准的日期有12月22日、12月23日、12月24日这3天。所以，就将这3天的数据聚集到一起，存入subset和subtargets变量中：

#将3个布尔型数组求与
bools = [any(tup) for tup in zip(bool1,bool2,bool3)]
#将相应的变量取出
subset = test_features.loc[rides[bools].index]
subtargets = test_targets.loc[rides[bools].index]
subtargets = subtargets['cnt']
subtargets = subtargets.values.reshape([len(subtargets),1])

将这3天的数据输入神经网络中，用前面定义的feature()函数读出隐含神经元的激活数值，存入results中。为了方便阅读，可以将归一化输出的预测值还原为原始数据的数值范围。

#将数据输入到神经网络中，读取隐含神经元的激活数值，存入results中
results = feature(subset.values, neu).data.numpy()
#这些数据对应的预测值（输出层）
predict = neu(torch.FloatTensor(subset.values)).data.numpy()
#将预测值还原为原始数据的数值范围
mean, std = scaled_features['cnt']
predict = predict * std + mean
subtargets = subtargets * std + mean

接下来，我们将隐含神经元的激活情况全部画出来。同时，为了比较，我们将这些曲线与模型预测的数值画在一起，可视化的结果如图3.25所示。

#将所有的神经元激活水平画在同一张图上
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(results[:,:],'.',alpha=0.1)
ax.plot((predict-min(predict))/(max(predict)-min(predict)),'bo-',label = 'Prediction')
ax.plot((subtargets-min(predict))/(max(predict)-min(predict)),'bo-',label = 'Real')
ax.plot(results[:,5],'.:',alpha=1, label='Neuro 6')

ax.set_xlim(right=len(predict))
ax.legend()
plt.ylabel('Normalized Values')

dates = pd.to_datetime(rides.loc[subset.index]['dteday'])
dates = dates.apply(lambda  d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24],rotation=45)

plt.show()

书上的图是这样的，Neuro 6比较契合Real，但是我按代码实际跑出来的每次不是在上面就是在下面完全不契合Real，也没查出来哪里有问题

上面这个应该是运行这么多词以来最好的效果了，但还是和书中差了很多

图3.25中方块曲线是模型的预测值，圆点曲线是实际值，不同颜色和线型的虚线是每个神经元的输出值。可以发现，Neuro 6的输出曲线与真实输出曲线比较接近。因此，我们可以认为该神经元对提高预测准确性有更大的贡献。

同时，我们还想知道Neuro 6为什么表现较好以及它的激活是由谁决定的。进一步分析它的影响因素，发现影响大小是通过输入层指向它的权重来判断的，如图3.26所示。

我们可以通过下列代码将这些权重可视化：

#找到与峰值对应的神经元，将其到输入层的权重输出
dic = dict(neu.named_parameters())
weights = dic['0.weight']
plt.plot(weights.data.numpy()[6,:],'o-')
plt.xlabel('Input Neurons')
plt.ylabel('Weight')

结果如图3.27所示。横轴代表不同的权重，也就是输入神经元的编号；纵轴代表神经网络训练后的连边权重。例如，横轴的第10个数对应输入层的第10个神经元，对应到输入数据中，是检测天气类别的类型变量。第32个数是小时数，也是类型变量，检测的是早6点这种模式。我们可以将其理解为，**纵轴的值为正就是促进，值为负就是抑制。**所以，图3.27中的波峰就是将该神经元激活，波谷就是神经元未激活。

我们看到，这条曲线在hr_12和weekday_0,6方面有较高的权重，这表示Neuro 6正在检测现在是不是中午12点，同时也在检测今天是不是周六或者周日。如果满足这些条件，则神经元就会被激活。与此相对的是，神经元在weathersit_3和hr_6这两个输入上的权重值为负值，并且刚好是低谷，这意味着该神经元会在下雨或下雪，以及早上6点的时候被抑制。**通过翻看日历可知，2012年的12月22日和23日刚好是周六和周日，因此Neuro 6被激活了，它们对正确预测这两天的正午高峰做了贡献。**但是，由于圣诞节即将到来，人们可能早早回去为圣诞做准备，因此这个周末比较特殊，并未出现往常周末的大量骑行需求，于是Neuro 6给出的激活值导致了正午单车预测值过高。

与此类似，我们可以找到导致12月24日早晚高峰预测值过高的原因。我们发现Neuro 4起到了主要作用，因为它的波动刚好跟预测曲线在24日的早晚高峰负相关，如图3.28所示。

同理，这个神经元对应的权重及其检测的模式如图3.29所示。

这个神经元检测的模式和Neuro 6相似却相反，它在早晚高峰的时候受到抑制，在节假日和周末激活。进一步考察从隐含层到输出层的连接，我们发现Neuro 4的权重为负数，但是这个负值又没有那么小。所以，这就导致了Neuro 4在12月24日早晚高峰的时候被抑制，但是这个信号抑制的效果并不显著，无法导致预测尖峰出现。

所以，我们分析出神经预测器Neu在这3天预测不准的原因是圣诞假期的反常模式。12月24日是圣诞夜，该网络对节假日早晚高峰抑制单元的抑制程度不够，所以导致了预测不准。如果有更多的训练数据，我们可以将Neuro 4的权重调节得更低，这样就有可能提高预测的准确率。

---

3.5 小结

本章我们以预测某地共享单车数量的问题作为切入点，介绍了人工神经网络的工作原理。通过调整神经网络中的参数，我们可以得到任意形状的曲线。接着，我们尝试用具有单输入、单输出的神经网络拟合共享单车数据并进行预测。

但是，预测的效果非常差。经过分析，我们发现，由于采用的特征变量为数据的编号，而这与单车的数量没有任何关系，因此完美拟合的假象只不过是一种过拟合的结果。所以，我们尝试了新的预测方式，利用每一条数据中的特征变量，包括天气、风速、星期几、是否是假期、时间点等特征来预测单车使用数量，并取得了成功。

在第二次尝试中，我们还学会了如何对数据进行划分，以及如何用PyTorch自带的封装函数来实现人工神经网络、损失函数以及优化器。同时，我们引入了批处理的概念，即将数据切分成批，在每一个训练周期中，都用一小批数据来训练神经网络并调整参数。这种批处理的方法既可以加速程序的运行，又能够让神经网络稳步地调节参数。

最后，我们对训练好的神经网络进行了剖析。了解了人工神经元是如何通过监测数据中的固有模式而在不同条件下激活的。我们也清楚地看到，神经网络之所以在一些数据上工作不好，是因为在数据中很难遇到假期这种特殊条件。

3.6 Q&A

Q：神经元是不是越多越好？

A：当然不是。神经网络模型的预测能力不只和神经元的个数有关，还与神经网络的结构和输入数据有关。

Q：在预测共享单车使用量的实验中，为什么要清空梯度？

A：如果不清空梯度，backward()函数是会累加梯度的。我们在进行一次训练后，就立即进行梯度反传，所以不需要系统累加梯度。不清空梯度有可能导致模型无法收敛。

Q：对于神经网络来说，也可以逼近非收敛函数吗？

A：在一定的闭区间里是可以的。因为在闭区间里，一个函数不可能无穷发散，总会有一个界限，那么就可以使用神经网络模型进行逼近。对于一个无穷的区间来说，神经网络模型就不行了，因为它用于拟合的神经元数量是有限的。

Q：在预测共享单车的例子中，模型对圣诞节期间的单车使用量预测得不够准确。是不是可以通过增加训练数据的方法提高神经网络预测的准确性？

A：这种做法是可行的。如果使用更多的包含圣诞节期间单车使用情况的训练数据训练模型，那么模型对圣诞节期间单车使用情况的预测会更加准确。

Q：既然预测共享单车使用量的模型可以被解析和剖析，那么是不是每个神经网络都可以这样剖析？

A：这个不一定。因为预测共享单车使用量的模型结构比较简单，隐藏神经元只有10个。**当网络模型中神经元的个数较多或者有多层神经元的时候，神经网络模型的某个“决策”会难以归因到单个神经元里。**这时就难以用“剖析”的方式来分析神经网络模型了。

Q：在训练神经网络模型的时候，讲到了“训练集/测试集=k”，那么比例[插图]是多少才合理，k对预测的收敛速度和误差有影响吗？

A：在数据量比较少的情况下，我们一般按照10∶1的比例来选择测试集；而在数据量比较大的情况下，比如数据有十万条以上，就不一定必须按照比例来划分训练集和测试集了。

---

本章总代码

import numpy as np
import pandas as pd
import torch
import torch.optim as optim
import matplotlib.pyplot as plt
#导入数据
data_path='D:\deepLearning\hour.csv'
#rides为一个dataframe对象
rides=pd.read_csv(data_path)
rides.head()#输出部分数据
counts = rides['cnt'][:50]#截取前50数据
# x = np.arange(len(counts))
# y=np.array(counts)#单车数量
# plt.figure(figsize=(10,7))
# plt.plot(x,y,'o-')
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.show()
#在这里，我们使用了pandas库，从CSV文件中快速导入数据到rides里面。
# rides可以按照二维表的形式存储数据，并可以像访问数组一样对其进行访问和操作。
# rides.head()的作用是打印输出部分数据记录
#之后，我们从rides的所有记录中选出前50条，并只筛选出cnt字段放入counts数组中。
# 这个数组就存储了前50条单车使用数量记录。接着，我们绘制前50条记录的图，如图3.13所示。
#准备好了数据，我们就可以用PyTorch来搭建人工神经网络了。
# 与第2章的线性回归例子类似，我们首先需要定义一系列的变量，包括所有连边的权重和偏置，并通过这些变量的运算让PyTorch自动生成计算图：

#输入变量，1，2，3...这样的一维数组
# x=torch.FloatTensor(np.arange(len(counts),dtype=float))/len(counts)
# #输出变量，他是从数据counts中读取的每一时刻的单车数，共50个数据点的一维数组，作为标准答案
# y=torch.FloatTensor(np.array(counts,dtype=float))
# sz=10#设置隐含神经元的数量
# #初始化输入层到隐含层的权重矩阵，它的尺寸是（1，10）
# weights = torch.randn((1,sz),requires_grad=True)
# #初始化隐含层节点的偏置向量，它是尺寸为10的一维向量
# biases = torch.randn((sz),requires_grad=True)
# #初始化从隐含层到输出层的权重矩阵，它的尺寸是（10，1）
# weights2 = torch.randn((sz,1),requires_grad=True)
# #设置好变量和神经网络的初始参数，接下来迭代地训练这个神经网络：
# learning_rate=0.001#设置学习率
# losses=[]#记录每一次迭代的损失函数值，以方便以后绘图
# x=x.view(50,-1)
# y=y.view(50,-1)
# predictions = 0
# for i in range(100000):
#     #从输入层到隐含层的计算
#     hidden = x * weights + biases
#     #此时 hidden变量的尺寸是（50，10）即50个数据点，10个隐含神经元
#     #将sigmoid函数应用在隐含层的每一个神经元上
#     hidden = torch.sigmoid(hidden)
#     #隐含层输出到输出层，计算得到最终预测值
#     predictions = hidden.mm(weights2)
#     #此时，predictions的尺寸为（50，1），即50个数据点的预测值
#     #通过与数据中的标准答案y进行比较，计算均方误差
#     y = y.view(50,1)
#     loss = torch.mean((predictions-y) ** 2)
#     #此时，loss为一个标量，即一个数
#     losses.append(loss.data.numpy())
#
#     if i % 10000 == 0:#每隔10000个周期打印一次损失函数数值
#         print('loss',loss)
#
#     # 接下来执行梯度下降算法，将误差反向传播
#     loss.backward()#对损失函数进行梯度反转
#     #利用上一步计算中得到的weights、biases等梯度信息更新weights和biases的数值
#     weights.data.add_(-learning_rate * weights.grad.data)
#     biases.data.add_(-learning_rate * biases.grad.data)
#     weights2.data.add_(-learning_rate * weights2.grad.data)
#
#     #清空所有变量的梯度值
#     weights.grad.data.zero_()
#     biases.grad.data.zero_()
#     weights2.grad.data.zero_()
#
# #在上面这段代码中，我们进行了100000步训练迭代。
# # 在每一次迭代中，我们都将50个数据点的x作为数组全部输入神经网络，
# # 并让神经网络按照从输入层到隐含层、再从隐含层到输出层的步骤，一步步完成计算，最终输出对50个数据点的预测数组prediction。
# #之后，计算prediction和标准答案y之间的误差，并计算出50个数据点的平均误差loss，
# # 这就是我们前面提到的损失函数L。接着，调用loss.backward()完成误差沿着神经网络的反向传播过程，
# # 从而计算出计算图上每一个叶节点的梯度更新数值，并记录在每个变量的.grad属性中。最后，我们用这个梯度数值来更新每个参数的数值，从而完成了一步迭代。
# #仔细对比这段代码和第2章中的线性回归代码就会发现，除了中间的运算过程和损失函数有所不同外，其他的操作全部相同。
# # 事实上，在本书中，几乎所有的机器学习案例都采用了这样的步骤，即前馈运算、反向传播计算梯度、根据梯度更新参数值。
#
# #我们可以打印出Loss随着一步步迭代下降的曲线，这可以帮助我们直观地看到神经网络训练的过程，如图3.14所示。
#
# plt.plot(losses)
# plt.xlabel('Epoch')
# plt.ylabel('Loss')
# plt.show()
# x_data = x.data.numpy() #获得x包裹的数据
# plt.figure(figsize=(10,7))
# xplot, = plt.plot(x_data,y.data.numpy(),'o')
# yplot, = plt.plot(x_data,predictions.data.numpy())
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.legend([xplot,yplot],['Data','Prediction under 1000000 epochs '])
# plt.show()
#
# counts_predict = rides['cnt'][50:100] #读取待预测的后面50个数据点
# x = torch.FloatTensor((np.arange(len(counts_predict),dtype=float)+len(counts))/len(counts))
# #读取后面50个点的y数值，不需要做归一化
# y = torch.FloatTensor(np.array(counts_predict,dtype=float))
# #用x预测y
# hidden = x.expand(sz,len(x)).t() *weights.expand(len(x),sz)#从输入层到隐含层的计算
# hidden = torch.sigmoid(hidden)#将sigmoid函数应用在隐含层的每一个神经元上
# predictions = hidden.mm(weights2)#从隐含层到输出层，计算得到最终预测值
# loss = torch.mean((predictions-y) ** 2)#计算预测数据上的损失函数
# print(loss)
#
# #将预测曲线绘制出来
# x_data = x.data.numpy()
# plt.figure(figsize=(10,7))
# xplot, = plt.plot(x_data,y.data.numpy(),'o')
# yplot, = plt.plot(x_data,predictions.data.numpy())
# plt.xlabel('X')
# plt.ylabel('Y')
# plt.legend([xplot,yplot],['Data','Prediction'])
# plt.show()

dummy_fields = ['season','weathersit','mnth','hr','weekday'] #所有类型编码变量的名称
for each in dummy_fields:
    #取出所有类型变量，并将它们转变为独热编码
    dummies = pd.get_dummies(rides[each],prefix=each,drop_first=False)
    #将新的独热编码变量与原有的所有变量合并到一起
    rides = pd.concat([rides,dummies],axis=1)

#将原来的类型变量从数据表中删除
fields_to_drop = ['instant','dteday','season','weathersit','weekday','atemp','mnth','workingday','hr']
data = rides.drop(fields_to_drop,axis=1)#将它们从数据库的变量中删除
# print(data)
quant_features = ['cnt','temp','hum','windspeed']
scaled_features = {}#将每一个变量的均值和方差都存储到scaled_features变量中
for each in quant_features:
    #计算这些变量的均值和方差
    mean, std = data[each].mean(),data[each].std()
    scaled_features[each] = [mean, std]
    #对每一个变量进行标准化
    data.loc[:,each] = (data[each] - mean)/ std

test_data = data[-21*24:]#选出训练集
train_data = data[:-21*24]#选出测试集
#目标列包含的字段
target_fields = ['cnt','casual','registered']
#将训练集划分成特征变量列和目标特征列
features, targets = train_data.drop(target_fields,axis=1),train_data[target_fields]
#将测试集划分成特征变量列和目标变量列
test_features, test_targets = test_data.drop(target_fields,axis=1),test_data[target_fields]
#将数据类型转换为Numpy数组
X = features.values #将数据从pandas dataframe 转化为Numpy
Y = targets['cnt'].values
Y = Y.astype(float)

Y = np.reshape(Y,[len(Y),1])
losses = []

#定义神经网络架构，features.shape[1] 个输入单元，10个隐含单元，1个输出单元
input_size = features.shape[1]
hidden_size = 10
output_size = 1
batch_size = 128
neu = torch.nn.Sequential(
    torch.nn.Linear(input_size,hidden_size),
    torch.nn.Sigmoid(),
    torch.nn.Linear(hidden_size,output_size),
)
cost = torch.nn.MSELoss()
optimizer = torch.optim.SGD(neu.parameters(),lr = 0.01)

#神经网络训练循环
losses = []
for i in range(1000):
    #每128个样本点划分为一批，在循环的时候一批一批地读取
    batch_loss = []
    # start 和 end 分别是提取一批数据的起始下标和终止下标
    for start in range(0,len(X),batch_size):
        end = start + batch_size if start + batch_size < len(X) else len(X)
        xx = torch.tensor(X[start:end], dtype=torch.float, requires_grad=True)
        yy = torch.tensor(Y[start:end], dtype=torch.float, requires_grad=True)
        predict = neu(xx)
        loss = cost(predict,yy)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        batch_loss.append(loss.data.numpy())

    #每隔100步输出损失值
    if i % 100 ==0:
        losses.append(np.mean(batch_loss))
        print(i,np.mean(batch_loss))

#打印输出损失值
plt.plot(np.arange(len(losses))*100,losses)
plt.xlabel('epoch')
plt.ylabel('MSE')
plt.show()

targets = test_targets['cnt'] #毒区测试集的cnt数值
targets = targets.values.reshape([len(targets),1])#将数据转换成合适的张量形式
targets = targets.astype(float) #保证数据为实数

x = torch.FloatTensor(test_features.values.astype(float))
y = torch.FloatTensor(targets)

#用神经网络进行预测
predict = neu(x)
predict = predict.data.numpy()

fig, ax =plt.subplots(figsize=(10,7))

mean, std =scaled_features['cnt']
ax.plot(predict * std + mean, label='Prediction',linestyle = '--')
ax.plot(targets * std + mean, label='Data',linestyle = '-')
ax.legend()
ax.set_xlabel('Date-time')
ax.set_ylabel('Counts')
dates = pd.to_datetime(rides.loc[test_data.index]['dteday'])
dates = dates.apply(lambda d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24],rotation=45)#rotation横坐标字体旋转45°

plt.show()

def feature(X,net):
    #定义一个函数，用于提取网络的权重信息
    #所有网络参数信息全部存储在Neu的named_parameters集合中
    X = torch.from_numpy(X).type(torch.FloatTensor)
    dic = dict(net.named_parameters())#从这个集合中提取数据
    weights = dic['0.weight' ]# 可以按照“层数.名称”来索引集合中的相应参数值
    biases = dic['0.bias']
    h = torch.sigmoid(X.mm(weights.t()) + biases.expand([len(X), len(biases)]))
    #隐含层计算过程
    return h#输出层的计算

bool1 = rides['dteday'] == '2012-12-22'
bool2 = rides['dteday'] == '2012-12-23'
bool3 = rides['dteday'] == '2012-12-24'

#将3个布尔型数组求与
bools = [any(tup) for tup in zip(bool1,bool2,bool3)]
#将相应的变量取出
subset = test_features.loc[rides[bools].index]
subtargets = test_targets.loc[rides[bools].index]
subtargets = subtargets['cnt']
subtargets = subtargets.values.reshape([len(subtargets),1])

#将数据输入到神经网络中，读取隐含神经元的激活数值，存入results中
results = feature(subset.values, neu).data.numpy()
#这些数据对应的预测值（输出层）
predict = neu(torch.FloatTensor(subset.values)).data.numpy()
#将预测值还原为原始数据的数值范围
mean, std = scaled_features['cnt']
predict = predict * std + mean
subtargets = subtargets * std + mean

#将所有的神经元激活水平画在同一张图上
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(results[:,:],'.',alpha=0.2)
ax.plot((predict-min(predict))/(max(predict)-min(predict)),'bo-',label = 'Prediction')
ax.plot((subtargets-min(predict))/(max(predict)-min(predict)),'ro-',label = 'Real')
ax.plot(results[:,3],'.:',alpha=1, label='Neuro 4')

ax.set_xlim(right=len(predict))
ax.legend()
plt.ylabel('Normalized Values')

dates = pd.to_datetime(rides.loc[subset.index]['dteday'])
dates = dates.apply(lambda  d: d.strftime('%b %d'))
ax.set_xticks(np.arange(len(dates))[12::24])
_ = ax.set_xticklabels(dates[12::24],rotation=45)

plt.show()

#找到与峰值对应的神经元，将其到输入层的权重输出
dic = dict(neu.named_parameters())
weights = dic['0.weight']
plt.plot(weights.data.numpy()[6,:],'o-')
plt.xlabel('Input Neurons')
plt.ylabel('Weight')
plt.show()