JLU数据结构荣誉课第七次实验课

目录

7-1 序列调度 (100 分)

7-2 最大最小差 (100 分)

7-3 二叉树最短路径长度 (100 分)

7-4 方案计数 (100 分)

---

7-1 序列调度 (100 分)

有一个N个数的序列A：1，2，……，N。有一个后进先出容器D，容器的容量为C。如果给出一个由1到N组成的序列，那么可否由A使用容器D的插入和删除操作得到。

输入格式:

第1行，2个整数T和C，空格分隔，分别表示询问的组数和容器的容量，1≤T≤10，1≤C≤N。

第2到T+1行，每行的第1个整数N，表示序列的元素数，1≤N≤10000。接下来N个整数，表示询问的序列。

输出格式:

T行。若第i组的序列能得到，第i行输出Yes；否则，第i行输出No,1≤i≤T。

输入样例：

2 2
5 1 2 5 4 3
4 1 3 2 4

 输出样例:

 No
Yes

思路：

这道题就是模拟一个栈（有容量限制），过程就是，循环将序列1-N入栈，当遇到栈顶元素与遍历到的所给序列元素相等时，就出栈，继续向后遍历所给序列，直至遍历结束。 详细思路与考虑情况请看代码：

#include<iostream>
#include<string.h>
using namespace std;
const int maxsize=20005;
int A[maxsize];
int B[maxsize];

int check(int C){
	int N;
	int top=0;
    scanf("%d",&N);
    for(int i=1;i<=N;i++)scanf("%d",&B[i]);
	int ent=1/*N个数，挨着来压入*/,ant=1;
	while(ent<=N){
    	A[++top]=ent++;
   // 	printf("*%d*",A[top]);
	   	if(top>C)return 0;
	    if(A[top]==B[ant]){
	   		while(top)
	   		{
	   			if(A[top--]!=B[ant++]){
	   				break;
				}
			}
		}
	}
	while(top){
	//	printf("%d****",top);
        if(A[top--]!=B[ant++]){
            return 0;
        }
    }
	return 1;
}
int main(){
	int T;
	int C;
	scanf("%d %d",&T,&C);
	for(int k=1;k<=T;k++)
	{
		memset(A,0,sizeof(A));
		memset(B,0,sizeof(B));
		int judge=check(C);
		if(judge==0)printf("No\n");
		else{
			printf("Yes\n");
		}
	}
	return 0;
} 

 

7-2 最大最小差 (100 分)

对n 个正整数，进行如下操作：每一次删去其中两个数 a 和 b，然后加入一个新数：a*b+1，如此下去直到 只剩下一个数。所有按这种操作方式最后得到的数中，最大的为max，最小的为min，计算max-min。

输入格式:

第1行：n，数列元素的个数，1<=n<=16。

第2行：n 个用空格隔开的数x，x<=10。

输出格式:

1行，所求max-min。

输入样例:

3
2 4 3

输出样例:

2 

思路：

这道题是比较简单的，我们不难得出，不断取序列中的两个最小值相乘+1，最后得到的是max，不断取序列中两个最大值相乘+1，得到的是min。这样就好办啦，我用了两个优先队列，大根堆，小根堆，分别保持递增递减序列 ，不断出队、入队就可以了。

代码如下：

#include<bits/stdc++.h>
using namespace std;
priority_queue <long long,vector<long long>,greater<long long> > Q1;
priority_queue <long long,vector<long long>,less<long long> > Q2;
int main(){
	long long n;
	scanf("%lld",&n);
	for(long long i=1;i<=n;i++){
		long long m;
		scanf("%lld",&m);
		Q1.push(m);
		Q2.push(m);
	}
	while(Q1.size()!=1){
		long long a=Q1.top();
		Q1.pop();
		long long b=Q1.top();
		Q1.pop();
		Q1.push(a*b+1);
	}
	while(Q2.size()!=1){
		long long a=Q2.top();
		Q2.pop();
		long long b=Q2.top();
		Q2.pop();
		Q2.push(a*b+1);
	}
	long long maxn=Q1.top();
	long long min=Q2.top();
	printf("%lld",maxn-min);
	return 0;
}

 

7-3 二叉树最短路径长度 (100 分)

给定一棵二叉树T，每个结点赋一个权值。计算从根结点到所有结点的最短路径长度。路径长度定义为：路径上的每个顶点的权值和。

输入格式:

第1行，1个整数n，表示二叉树T的结点数，结点编号1..n，1≤n≤20000。

第2行，n个整数，空格分隔，表示T的先根序列，序列中结点用编号表示。

第3行，n个整数，空格分隔，表示T的中根序列，序列中结点用编号表示。

第4行，n个整数Wi，空格分隔，表示T中结点的权值，-10000≤Wi≤10000，1≤i≤n。

输出格式:

1行，n个整数，表示根结点到其它所有结点的最短路径长度。

输入样例:

4
1 2 4 3
4 2 1 3
1 -1 2 3

输出样例:

1 0 3 3

思路：

这道题的难点就是根据二叉树的先根序和中根序唯一确定建立一个二叉树。关键要抓住先根序的第一个结点就是这棵树的根，中根序是可以将左右子树分开，这两个结合起来，就可以构建二叉树了，递归构建左右子树。 

建树代码：

int pLeft=1,iLeft=1;
int pRight=n,iRight=n;


tree root;
Build_Tree(pLeft,pRight,iLeft,iRight,root);

void Build_Tree(int pLeft, int pRight, int iLeft, int iRight,tree &root)
{
	if (pLeft>pRight||iLeft>iRight)  root=NULL;
	else
	{
		root = new TreeNode;
		root->lchild=NULL;
		root->rchild=NULL;
		int remark = -1;
		for (int i = iLeft; i <= iRight; i++)
		{
			if (inorder[i] == preorder[pLeft])
			{
				remark = i;
				break;
			}
		}
		root->Veradj = inorder[remark];
		Build_Tree(pLeft + 1, pLeft + remark - iLeft, iLeft, remark - 1,root->lchild);
		Build_Tree(pRight + remark - iRight + 1, pRight, remark + 1, iRight,root->rchild);
	}
}

之后求根节点到每个结点的最短路径长度，就是深度优先遍历，然后将根结点到某个节点v0经过的所有结点权值加起来，就是根结点到v0的最短路径长度（唯一的，因为这是一棵树，根结点到其他结点都是只有一条路径。）

代码如下：

#include<iostream>
using namespace std;
const int maxsize=20005;
typedef struct TreeNode
{
    int Veradj;
    TreeNode* lchild;
    TreeNode* rchild;
}*tree;
int preorder[maxsize];
int inorder[maxsize];
int cost[maxsize];


void Build_Tree(int pLeft, int pRight, int iLeft, int iRight,tree &root)
{
	if (pLeft>pRight||iLeft>iRight)  root=NULL;
	else
	{
		root = new TreeNode;
		root->lchild=NULL;
		root->rchild=NULL;
		int remark = -1;
		for (int i = iLeft; i <= iRight; i++)
		{
			if (inorder[i] == preorder[pLeft])
			{
				remark = i;
				break;
			}
		}
		root->Veradj = inorder[remark];
		Build_Tree(pLeft + 1, pLeft + remark - iLeft, iLeft, remark - 1,root->lchild);
		Build_Tree(pRight + remark - iRight + 1, pRight, remark + 1, iRight,root->rchild);
	}
}

void shortestroad(tree root){
	if(root->lchild!=NULL){ 
	    cost[root->lchild->Veradj]=cost[root->Veradj]+cost[root->lchild->Veradj];
  //    printf("*%d*",cost[1]);
		shortestroad(root->lchild);
	} 
	if(root->rchild!=NULL){
	    cost[root->rchild->Veradj]=cost[root->Veradj]+cost[root->rchild->Veradj]; 
		shortestroad(root->rchild);
	} 
}
int main(){
     int n;
	 scanf("%d",&n);
	 for(int i=1;i<=n;i++){
	 	scanf("%d",&preorder[i]);
	 }
	 for(int i=1;i<=n;i++){
	 	scanf("%d",&inorder[i]);
	 }
	 int pLeft=1,iLeft=1;
	 int pRight=n,iRight=n;
	 for(int i=1;i<=n;i++){
	 	scanf("%d",&cost[i]);
	 }
	 tree root;
	 Build_Tree(pLeft,pRight,iLeft,iRight,root);
//	 printf("%d",root->Veradj);
	 shortestroad(root);
	 for(int i=1;i<=n;i++){
	 	printf("%d%c",cost[i],i==n?'\n':' ');
	 }
	 return 0;
} 

 

7-4 方案计数 (100 分)

组装一个产品需要 n 个零件。生产每个零件都需花费一定的时间。零件的生产可以并行进行。有些零件的生产有先后关系，只有一个零件的之前的所有零件都生产完毕，才能开始生产这个零件。如何合理安排工序，才能在最少的时间内完成所有零件的生产。在保证最少时间情况下，关键方案有多少种，关键方案是指从生产开始时间到结束时间的一个零件生产序列，序列中相邻两个零件的关系属于事先给出的零件间先后关系的集合，序列中的每一个零件的生产都不能延期。

输入格式:

第1行，2个整数n和m，用空格分隔，分别表示零件数和关系数，零件编号1..n，1≤n≤10000, 0≤m≤100000 。

第2行，n个整数Ti，用空格分隔，表示零件i的生产时间，1≤i≤n，1≤Ti≤100 。

第3到m+2行，每行两个整数i和j，用空格分隔，表示零件i要在零件j之前生产。

输出格式:

第1行，1个整数，完成生产的最少时间。

第2行，1个整数，关键方案数，最多100位。

如果生产不能完成，只输出1行，包含1个整数0.

输入样例:

4 4
1 2 2 1
1 2
1 3
2 4
3 4
 

输出样例:

4
2

 思路：

这道题，可谓是多磨多难呀。

其实读题之后，大概想法就有了，先拓扑排序判断能否完成此次生产。在求关键路径，但是，题目中所描述的图是点权图，所以要考虑到把他转化成边权图求（是我个人观点，也有其他同学不转就可以求出来的）。所以，转化的话，就需要引入虚源，和虚汇，把每个关键方案的开始连到虚源点，每个关键方案的结束连到虚汇点，这样，就算所给的零件生产顺序组成的图是不连通的，也能当作连通图处理了。

拿样例来举个例子：

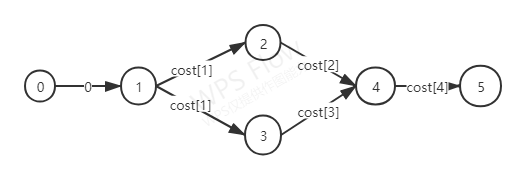
结点0就是虚源点，结点5就是虚汇点，这个图中的边，其实是题目中已知的点转化来的，我把边的起始顶点的权赋值给了边。

处理完这个，然后去求关键路径。之后用计数原理求关键方案数即可。注意到的一点是，关键方案数最多有一百位，这里要用到高精度乘法！！！！ 

代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long int ll;
const int maxsize=10005;
int count1[maxsize];//记录所顶点的入度 
int count2[maxsize];//记录所有点的入度 
int cost[maxsize];
ll Branch[maxsize];
vector<int>mp[maxsize];
vector<pair<int,int> >Trans[maxsize];
int TopoOrder(int n);// 拓扑排序算法：AOV网 
void CriticalPath(int n);//关键路径：AOE网 
void Transform(int);//转换点权图为边权图 
void mutiply(int x);

int sum[105];
int TopoOrder(int n){// 拓扑排序算法：AOV网 
	int i,j,k;
	for(i=1;i<=n;i++){
		vector<int>::iterator ik;
		for(ik=mp[i].begin();ik!=mp[i].end();ik++)
		    count1[(*ik)]++;
	}
	for(int i=1;i<=n;i++){
		if(count1[i]==0){//手动加虚源点
			Trans[0].push_back(make_pair(i,0));
		}
	}
	stack<int> S;
	for(i=1;i<=n;i++){
		if(count1[i]==0) 
		   S.push(i);  
	}
	for(i=1;i<=n;i++){
		if(S.empty()) return -1;
		j=S.top();S.pop();
		vector<int>::iterator ik;
		for(ik=mp[j].begin();ik!=mp[j].end();ik++){
			k=(*ik);
			count1[k]--;
			if(count1[k]==0){
			    S.push(k);
			}
		}
	}
	return 1;
}
int lenth=1;
void mutiply(int x){
	int ant=0,ent; //刚开始进位为0；
	for(int j=1;j<=lenth;j++){ 
	    ent=x*sum[j]+ant;
		if(ent>9){
			//printf("和：*%d*\n",ent);
			ant=ent/10;
			sum[j]=ent%10;
			//printf("个位：*%d*\n",x[j]);
		    //printf("进位:*%d\n*",ant);
		}
		else{
			sum[j]=ent;
			ant=0;
		}
	}
	if(ant!=0){
		while(ant>0){
			lenth++;
			sum[lenth]=ant%10;
			ant=ant/10;
		}
	}
}
void CriticalPath(int n){//关键路径：AOE网 
	int i,j,k;
	int ve[maxsize],vl[maxsize];//ve[]是最早发生时间，vl[]是最迟发生时间 
	//计算事件的最早发生时间
	for(i=0;i<=n+1;i++) ve[i]=0;
	for(i=1;i<=n;i++){ 
	    vector<pair<int,int> >::iterator it; 
		for(it=Trans[i].begin();it!=Trans[i].end();it++){
			k=(*it).first;
			if(ve[i]+(*it).second>ve[k])
			    ve[k]=ve[i]+(*it).second;
		}
	}
	//计算事件最迟发生时间 
	for(i=1;i<=n+1;i++) vl[i]=ve[n+1];  
	for(i=n+1;i>=0;i--){
		vector<pair<int,int> >::iterator it; 
		for(it=Trans[i].begin();it!=Trans[i].end();it++){
			k=(*it).first;
			if(vl[k]-(*it).second<vl[i])
			    vl[i]=vl[k]-(*it).second;
		}
	}
	printf("%d\n",vl[n+1]);
	for(i=0;i<=n;i++){
		vector<pair<int,int> >::iterator it; 
		for(it=Trans[i].begin();it!=Trans[i].end();it++){
			k=(*it).first;
			int e=ve[i];
			int l=vl[k]-(*it).second;
			if(l==e){
				Branch[i]++;
			}
		}
	}
	sum[1]=1;
	for(int i=0;i<=n;i++){
		if(Branch[i]!=0){
		//	printf("*%d*",Branch[i]);
			mutiply(Branch[i]);
		}
	}
	for(int i=lenth;i>=1;i--){
		printf("%d",sum[i]);
	}
	printf("\n");
}
void Transform(int n){
	for(int i=1;i<=n;i++){
	    vector<int>::iterator it;
    	for(it=mp[i].begin();it!=mp[i].end();it++){
	    	Trans[i].push_back(make_pair((*it),cost[i]));
    	}	
	}
	for(int i=1;i<=n;i++){//手动加虚汇点
		if(count2[i]==0){
			Trans[i].push_back(make_pair(n+1,cost[i]));
		}
	}
} 

int main(){
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d",&cost[i]);
	}
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		mp[u].push_back(v);
		count2[u]++;
	}
	int p=TopoOrder(n);
	if(p==-1){
		printf("0");
	}
	else{
		Transform(n); 
		CriticalPath(n);
	}
	return 0;
}