无监督学习算法

一、聚类算法

聚类作用：

• 知识发现事物之间的潜在关系
• 异常值检测
• 特征提取 数据压缩的例子

有监督与无监督学习：

• 有监督:

1.  给定训练集 X 和 标签Y 选择模型
2.  学习(目标函数的最优化)
3. 生成模型(本质上是一组参数、方程)
4. 根据生成的一组参数进行预测分类等任务

• 无监督:

1. 拿到的数据只有X ，没有标签，只能根据X的相似程度做一些事情。
2. Clustering 聚类

         对于大量未标注的数据集，按照内在相似性来分为多个类别(簇) 目标:类别内相似度大，类别间相似小。

        也可以用来改变数据的维度，可以将聚类结果作为一个维度添加到训练数据中。

    3.降维算法，数据特征变少

聚类算法

二、Kmeans

2.1 聚类原理

• 将N个样本映射到K个簇中
• 每个簇至少有一个样本

2.2 基本思路

• 先给定K个划分，迭代样本与簇的隶属关系，每次都比前一次好一些
• 迭代若干次就能得到比较好的结果

2.3 算法步骤

1. 选择K个初始的簇中心-----》怎么选?
2. 逐个计算每个样本到簇中心的距离，将样本归属到距离最小的那个簇中心的簇中
3. 每个簇内部计算平均值，更新簇中心
4. 开始迭代

聚类过程如下:

聚类执行过程：

2.4 KMeans优缺点

优点:

1. 简单，效果不错

缺点：

1. 对异常值敏感
2. 对初始值敏感
3. 对某些分布聚类效果不好

2.5 Kmeans损失函数

2.6 Kmeans使用

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd

# 需要将亚洲国家队，分成三个类别
# 只有历年的统计数据，没有目标值(类别，等级)

data = pd.read_csv('./AsiaFootball.txt')

data

# 执行多次，分类结果会有所不同
kmeans = KMeans(n_clusters=3)
# 无监督，只需要给数据X就可以
kmeans.fit(data.iloc[:,1:])

y_ = kmeans.predict(data.iloc[:,1:])

# 聚类算法预测、划分的类别

c = data['国家'].values
for i in range(3):

        cond = y_ == i#索引条件

        print('类别是%d的国家有:'%(i),c[cond])

plt.rcParams['font.family'] = 'STKaiti'
fig = plt.figure(figsize=(12,9))
ax = plt.axes(projection = '3d')
ax.scatter(data.iloc[:,1],data.iloc[:,2],data.iloc[:,3],c = y_,s = 100)

ax.set_xlabel('2006年世界杯',fontsize = 18)

ax.set_ylabel('2010年世界杯',fontsize = 18)

ax.set_zlabel('2007亚洲杯',fontsize = 18)

# 调整视图角度
ax.view_init(elev = 20,azim = -60)

2.7 Kmeans聚类算法K值选择

import numpy as np
from sklearn import datasets
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# 聚类:轮廓系数，对聚类的评价指标，对应数学公式

from sklearn.metrics import silhouette_score

# 创建数据
# 假数据，数据X划分成3类
X,y = datasets.make_blobs(centers=3)

plt.scatter(X[:,0],X[:,1],c = y)

# 指定不同的k，寻找最佳聚类类别数目
# 可以画图，一目了然，数据简单，属性只有两个，所以可以画图

# 属性多，无法可视化，评价指标
# 轮廓系数
plt.rcParams['font.sans-serif'] = 'KaiTi'

plt.rcParams['font.size'] = 18

plt.rcParams['axes.unicode_minus'] = False

score = []
for i in range(2,7):

        kmeans = KMeans(n_clusters=i)

        kmeans.fit(X)
        y_ = kmeans.predict(X) # 预测类别 == 标签

        score.append(silhouette_score(X,y_))

plt.plot(range(2,7),score)
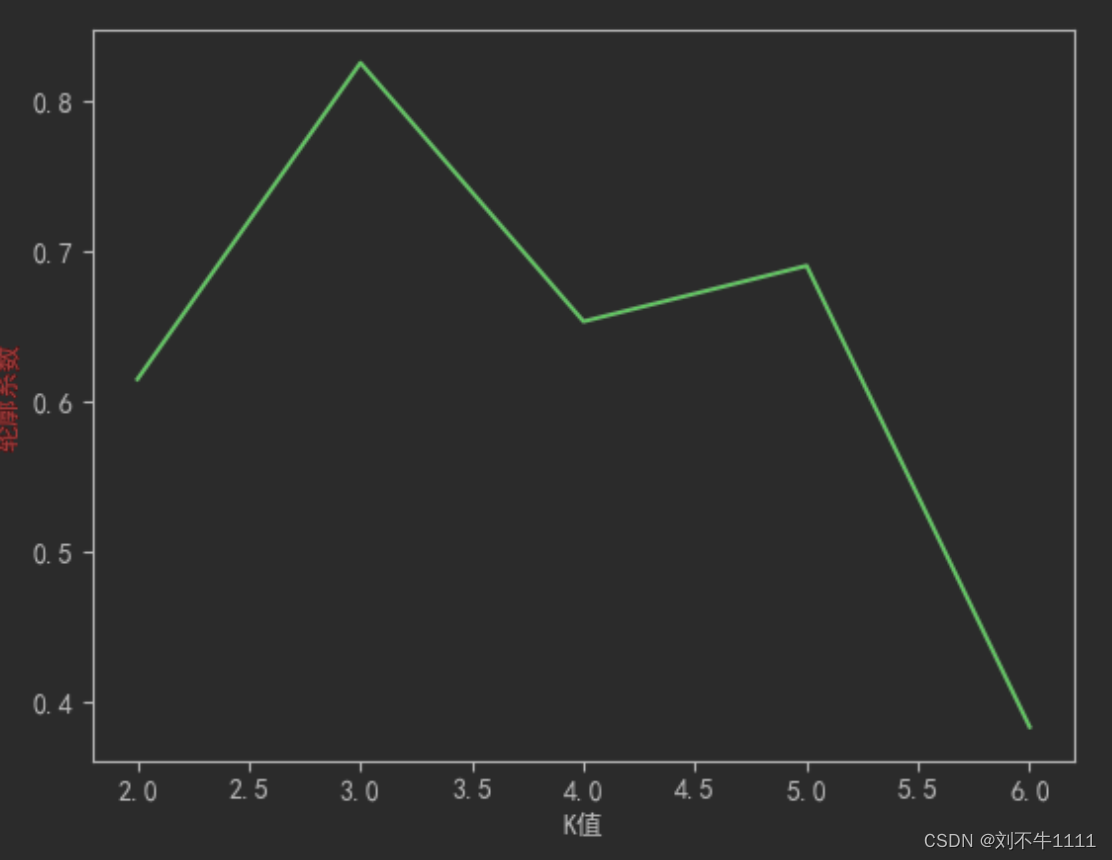
plt.xlabel('K值')
plt.ylabel('轮廓系数',c = 'red')

# 结论:，当k值是3的时候，轮廓系数最大，这个时候，说明划分效果最好!

效果图如下:(注意数据随机生成，数据展示的图片效果不是固定的~)

from sklearn.metrics import adjusted_rand_score# 调整兰德系数

score = []
for i in range(2,7):

        kmeans = KMeans(n_clusters=i)

        kmeans.fit(X)
        y_ = kmeans.predict(X)# 预测类别 == 标签

        score.append(adjusted_rand_score(y,y_))

plt.plot(range(2,7),score)
plt.xlabel('K值')
plt.ylabel('调整兰德系数',c = 'red')

# 结论:，当k值是3的时候，轮廓系数最大，这个时候，说明划分效果最好!

Kmeans图像压缩

import matplotlib.pyplot as plt # plt 用于显示图片

from sklearn.cluster import KMeans
import numpy as np

plt.figure(figsize=(8,4))

# 加载图片显示原图
pixel = plt.imread('11-bird.png')

plt.subplot(1,2,1)

plt.imshow(pixel)

# 聚类运算，压缩图片
pixel = pixel.reshape((128*128 , 3))

kmeans = KMeans(n_clusters=8).fit(pixel)

# 聚类结果合成新图片
newPixel = kmeans.cluster_centers_[kmeans.labels_].reshape(128,128,3)

plt.subplot(1,2,2)
plt.imshow(newPixel)

        

三、DBSCAN

3.1  DBSCAN概念

3.2 DBSCAN算法原理

网站动画解析：https://www.naftaliharris.com/blog/visualizing-dbscan-clustering/

3.3 DBSCAN参数解析

3.4 DBSCAN使用示例

import numpy as np
from sklearn import datasets
from sklearn.cluster import KMeans,DBSCAN
import matplotlib.pyplot as plt

X,y = datasets.make_circles(n_samples=1000,noise=0.05,factor = 0.5)

# centers = [(1.5,1.5)] 元组，代表着，中心点的坐标值
# y1一类:0 + 2

X1,y1 = datasets.make_blobs(n_samples=500,n_features=2,centers=[(1.5,1.5)],cluster_std=0.2)

# 将circle和散点进行了数据合并
X = np.concatenate([X,X1])
y = np.concatenate([y,y1 + 2]) plt.scatter(X[:,0],X[:,1],c = y)

# 根据距离，划分‘势力范围’
kmeans = KMeans(3)
kmeans.fit(X)
y_ = kmeans.labels_ plt.scatter(X[:,0],X[:,1],c = y_)

dbscan = DBSCAN(eps = 0.2,min_samples=3)
dbscan.fit(X)
y_ = dbscan.labels_
plt.scatter(X[:,0],X[:,1],c = y_)

四、分层聚类

4.1 算法介绍

4.2 算法原理

4.3 参数介绍

4.4 分层算法使用

import numpy as np
import matplotlib.pyplot as plt
import mpl_toolkits.mplot3d.axes3d as p3
from sklearn.cluster import AgglomerativeClustering
from sklearn.datasets import make_swiss_roll

X,y = datasets.make_swiss_roll(n_samples=1500,noise = 0.05)
fig = plt.figure(figsize=(12,9))
a3 = fig.add_subplot(projection = '3d')
a3.scatter(X[:,0],X[:,1],X[:,2],c = y)
a3.view_init(10,-80)

# Kmeans只负责分类，随机性，类别是数字几，不固定

clf = KMeans(n_clusters=6)
clf.fit(X)
y_ = clf.labels_ # y_ = clf.predict(x)

fig = plt.figure(figsize=(12,9))

a3 = plt.subplot(projection = '3d')

a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)

a3.view_init(10,-80)

# 分层聚类

agg = AgglomerativeClustering(n_clusters=6,linkage='ward')# 最近的距离，作为标准， agg.fit(X)
y_ = agg.labels_
fig = plt.figure(figsize=(12,9))

a3 = plt.subplot(projection = '3d')

a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)

a3.view_init(10,-80)

对于这种非欧几何的数据下，可见如果没有设置连接性约束，将会忽视其数据本身的结构，强制在欧式
空间下聚类，于是很容易形成了上图这种跨越流形的不同褶皱。

分层聚类改进(连接性约束，对局部结构进行约束)

from sklearn.neighbors import kneighbors_graph# graph图形的意思
# 邻居数量变少，认为，条件宽松
conn = kneighbors_graph(X,n_neighbors=10) #采用邻居，进行约束
agg = AgglomerativeClustering(n_clusters=6,connectivity=conn,linkage='ward')# 最 近的距离，作为标准，

agg.fit(X)

y_ = agg.labels_

fig = plt.figure(figsize=(12,9))

a3 = fig.add_subplot(projection = '3d')

a3.scatter(X[:,0],X[:,1],X[:,2],c = y_)

a3.view_init(10,-80)

五、数据降维

5.1 概念介绍

5.2 降维方法介绍

六、PCA（主成分分析）降维算法

6.1 概念介绍

6.2 PCA降维原理

协方差和散度矩阵：

A = np.random.randint(0,10,size = (3,3)) # 协方差
cov = np.cov(A,rowvar=True)
# 散度矩阵

B = (A - A.mean(axis = 1).reshape(-1,1))

scatter = B.dot(B.T)

display(A,cov,scatter)

特征值分解矩阵原理：

SVD分解矩阵原理

6.3 PCA算法实现方式

6.3.1 基于特征值分解协方差矩阵实现PCA算法

from sklearn.decomposition import PCA
from sklearn import datasets

# 物理意义的特征
x,y = datasets.load_iris(return_X_y=True)
display(x[:5])

# 1、去中心化
B = X - X.mean(axis = 0)

B[:5]

# 2、协方差
# 方差是协方差特殊形式
# 协方差矩阵
V = np.cov(B,rowvar=False,bias = True)

# 3、协方差矩阵的特征值和特征向量

# 特征值和特征向量矩阵的概念

eigen,ev = np.linalg.eig(V)

display(eigen,ev)

# 4、降维标准，2个特征，选取两个最大的特征值所对应的特征的特征向量

# 百分比，计算各特征值，占权重，累加可以
cond = (eigen/eigen.sum()).cumsum() >= 0.98
index = cond.argmax()

ev = ev[:,:index + 1]

# 5、进行矩阵运算

pca_result = B.dot(ev)

# 6、标准化
pca_result = (pca_result -pca_result.mean(axis = 0))/pca_result.std(axis = 0)
pca_result[:5]

6.3.2 基于SVD分解协方差矩阵实现PCA算法

from scipy import linalg
n_components_ = 3
X,y = datasets.load_iris(return_X_y = True)

# 1、去中心化
mean_ = np.mean(X, axis=0)

X -= mean_

# 2、奇异值分解
U, S, Vt = linalg.svd(X, full_matrices=False)

# 3、符号翻转(如果为负数，那么变成正直)
max_abs_cols = np.argmax(np.abs(U), axis=0)
signs = np.sign(U[max_abs_cols, range(U.shape[1])])

U *= signs

# 4、降维特征筛选
U = U[:, :n_components_]

# 5、归一化
# U = (U - U.mean(axis = 0))/U.std(axis = 0)

U *= np.sqrt(X.shape[0] - 1)
U[:5]

七、LDA（线性判别）降维算法

7.1 概念介绍

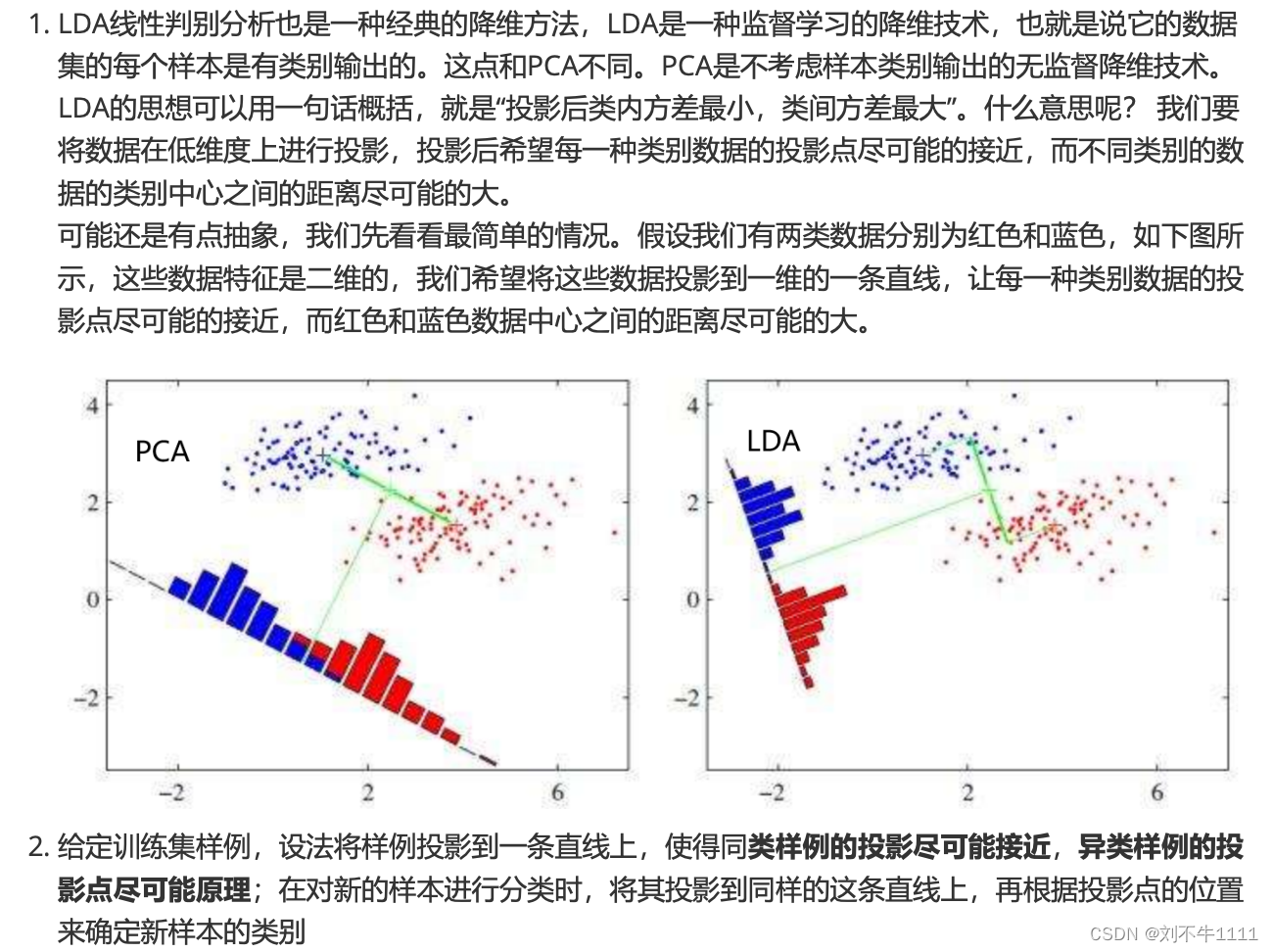
7.2 LDA算法实现方式

import numpy as np
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from sklearn import datasets
# scipy这个模块下的线性代数子模块
from scipy import linalg

# 加载数据
X,y = datasets.load_iris(return_X_y=True)

X[:5]

# 1、总的散度矩阵
# 协方差
St = np.cov(X.T,bias = 1)

St

# 2、类内的散度矩阵
# Scatter散点图，within(内)
Sw = np.full(shape = (4,4),fill_value=0,dtype=np.float64)

for i in range(3):

        Sw += np.cov(X[y == i],rowvar = False,bias = 1)

Sw/=3

Sw

# 3、计算类间的散度矩阵

# Scatter between

Sb = St - Sw
Sb

# 4、特征值，和特征向量
eigen,ev = linalg.eigh(Sb,Sw)
ev = ev[:, np.argsort(eigen)[::-1]][:,:2]

ev

# 5、删选特征向量，进行矩阵运算

X.dot(ev)[:5]