计算机组成原理-4-数据信息的校验

1、码距

• 任意两个合法编码间不同的二进制位数，比如10101和00110从高位到低位对应的第1位，第4位，第5位不同，因此码距为3。
• 码距越大，抗干扰能力、纠错能力越强，数据冗余越大，编码效率越低
• 选择码距应考虑信息出错概率和系统容错率。

2、奇偶校验

2.1 简单奇偶校验

编码规则：

增加一位校验位P，使得最终的校验码（由原数据与校验位P拼接而成）中数字1的个数为奇数或者偶数，最小码距为2。

奇校验：

最终的校验码中数字1的个数为奇数，0000 -> 00001   (奇校验，也即校验位P应该为1)    

偶校验:

最终的校验码中数字1的个数为偶数 ，0000 ->00000   (偶校验，也即校验位P应该为0)    

原始数据（7位）	奇校验码（8位）	偶校验码（8位）
0000000	00000001	00000000
1111111	11111110	11111111
1011001	10110011	10110010

校验位P与检错码G：

上述红色字体的数字为得到的校验位，但都是基于人工完成的，对于机器而言如何得到正确的校验位？假设原始数据有8位

偶校验：

如果采用偶校验，则P=D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8。

偶校验对应的检错码:G=P+D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8

奇校验：

如果采用奇校验，则P=

奇校验对应的检错码:G=

不论是奇校验还是偶校验，G=1: 数据一定出错；

G=0:较大概率正常(比如有偶数个数据出错，得到的G结果同样为0)。

校验位P的逻辑表达式：

ps：校验位P的逻辑表达式的由来，首先我们要知道两个基础知识

①对于偶校验，最终的校验码中数字1的个数为偶数

②对于异或运算“⊕”，具有相同为0，相反为1的原则，即1⊕1=0，0⊕0=0，1⊕0=1，0⊕1=1

---

公式推导：

1、偶校验中，对于D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8⊕P中，有偶数个1，0的数量不确定。

2、偶数个1异或之后一定为0，0再与其他为0的数据进行异或之后一定为0。                   

ps:不论是奇数个0还是偶数个0之间的异或结果都为0，比如 0⊕0=0,0⊕0⊕0=0           

因此:D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8⊕P=0。

3、根据异或规则，P需与D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8相等，才可保证结果为0，因此对于偶校验来说，P=D1⊕D2⊕D3⊕D4⊕D5⊕D6⊕D7⊕D8，奇校验同理。

优缺点：

• 编码与检错简单 
• 编码效率高
• 不能检测偶数位错误, 无错结论不可靠，是一种错误检测码
• 不能定位错误，因此不具备纠错能力

2.2 行列奇偶校验

2.2.1特点

• 也叫做二维奇偶校验，在简单奇偶校验的基础上做了一些改进，别名：双向奇偶校验、方块校验 、垂直水平校验、二维奇偶校验。
• 简单来说，行列奇偶校验对多组数据进行检测，组与组之间的数据按行排列，原本简单奇偶校验只是每组增加一个校验位P，而行列奇偶校验除了每组(每行)增加一个校验位P之外，每一列的数据（好像形成了一个“新组”）也为其增加一个校验位P。 

2.2.2 检错并纠错

行列奇偶校验可检错并纠错

如下图，假设红色数据为出错了的结果，以下是1位~4位出错的一些极端情况。

1位数据出错可纠错 根据第三行行校验G和第三列列校验G的的结果能同时判定第三行，第三列的数据有误，因此可以准确定位即可纠错（取反即可）	2位数据出错可检错 图中第三行行校验由于是两位数据出错，G=0，判定为没出错。但在列校验中，第3列和第7列的列校验能够检测数据出错
3位数据出错可检错 第4行有数据出错、第7列有数据出错
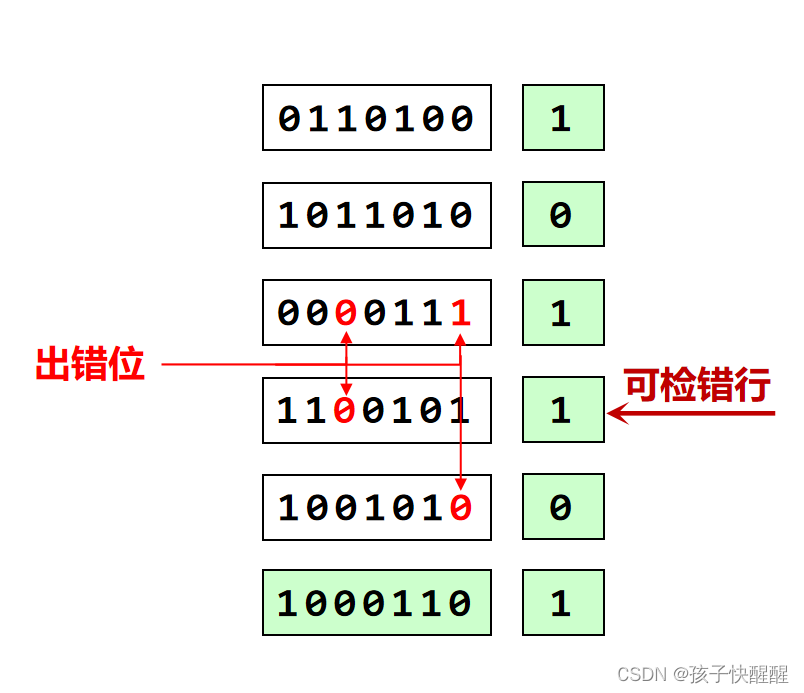
4位数据出错可检错行	4位数据出错无法检错

 当四个出错的数据正好位于形成的矩形顶点时，完全无法检错。

3、海明校验

3.1特点

• 海明校验拥有多个奇偶校验组 既能检错，也能纠错
• 最小码距为3
• 增加冗余码（校验位，r位），有效信息(k位) ，r需要满足以下公式，N=k+r ≤

3.2校验规则

(1)设k+r位海明码从左到右依次为第1，2，3...， k+r位，r位校验位记 为Pi（i=1,2…，r)，分别位于k+r位海明编码的第 （i=1，2，…，r) 位上，其余位依次放置被校验的数据位；

(2)(7，4)海明校验码中校验位和被校验信息位的排列如下：

海明码位号 Hj	1	2	3	4	5	6	7	8	9	10	11
P和b的分布	P1	P2	b1	P3	b2	b3	b4	P4	b5	b6	b7

(3) H j 位的 数据 被编号小于j的若干个海明位号之和等于j的 校验位 所校验 ,如：

P1=b1 ⊕ b2 ⊕ b4 ⊕ b5 ⊕ b7

P2=b1 ⊕ b3 ⊕ b4 ⊕ b6 ⊕ b7

P3=b2 ⊕ b3 ⊕ b4

P4=b5 ⊕ b6 ⊕ b7

(4) 设置指错字G 4 G 3 G 2 G 1

G 4 = P4  ⊕  b5 ⊕  b6 ⊕  b7

G 3 = P3  ⊕  b2 ⊕  b3 ⊕  b4

G 2 = P2  ⊕  b1  ⊕  b3 ⊕  b4 ⊕  b6 ⊕  b7

G 1 = P1  ⊕ b1  ⊕  b2 ⊕  b4 ⊕  b5 ⊕  b7

G 4 G 3 G 2 G 1 为0则表明无错误，反之指出出错位的海明码位号。

3.3海明举例

设8位有效信息为01101110，试写出它的海明校验码。给出过程，说明分组检测方式，并给出指错字及其逻辑表达式。如果接收方接收到的有效信息变为01101111，说明如何定位错误并纠正错误。

设8位有效信息01101110=D1D2D3D4D5D6D7D8,被校验位有8位，设校验位有r位，因为8+r≤2^r-1，所以r=4.

P1=D1⨁D2⨁D4⨁D5⨁D7＝0⨁1⨁0⨁1⨁1＝1 

P2=D1⨁D3⨁D4⨁D6⨁D7＝0⨁1⨁0⨁1⨁1＝1 

P3=D2⨁D3⨁D4⨁D8＝1⨁1⨁0⨁0＝0 

P4=D5⨁D6⨁D7⨁D8＝1⨁1⨁1⨁0＝1

海明码为：110011011110

接收方接收到的信息只有 D8 位出错，因此接收到的海明编码为 110011011111，

G1＝P1⨁D1⨁D2⨁D4⨁D5⨁D7＝1⨁0⨁1⨁0⨁1⨁1＝0 

G2＝P2⨁D1⨁D3⨁D4⨁D6⨁D7＝1⨁0⨁1⨁0⨁1⨁1＝0 

G3＝P3⨁D2⨁D3⨁D4⨁D8＝0⨁1⨁1⨁0⨁1＝1

G4＝P4⨁D5⨁D6⨁D7⨁D8＝1⨁1⨁1⨁1⨁1＝1

指错码G4G3G2G1 ＝1100＝12，如果假设只有一位错，则是海明码 H12 出错，也就是 D8 出错，将对应位取反即可。