L1-006 连续因子

一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：

输入在一行中给出一个正整数 N（1<N<231）。

输出格式：

首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。

输入样例：

630

输出样例：

3
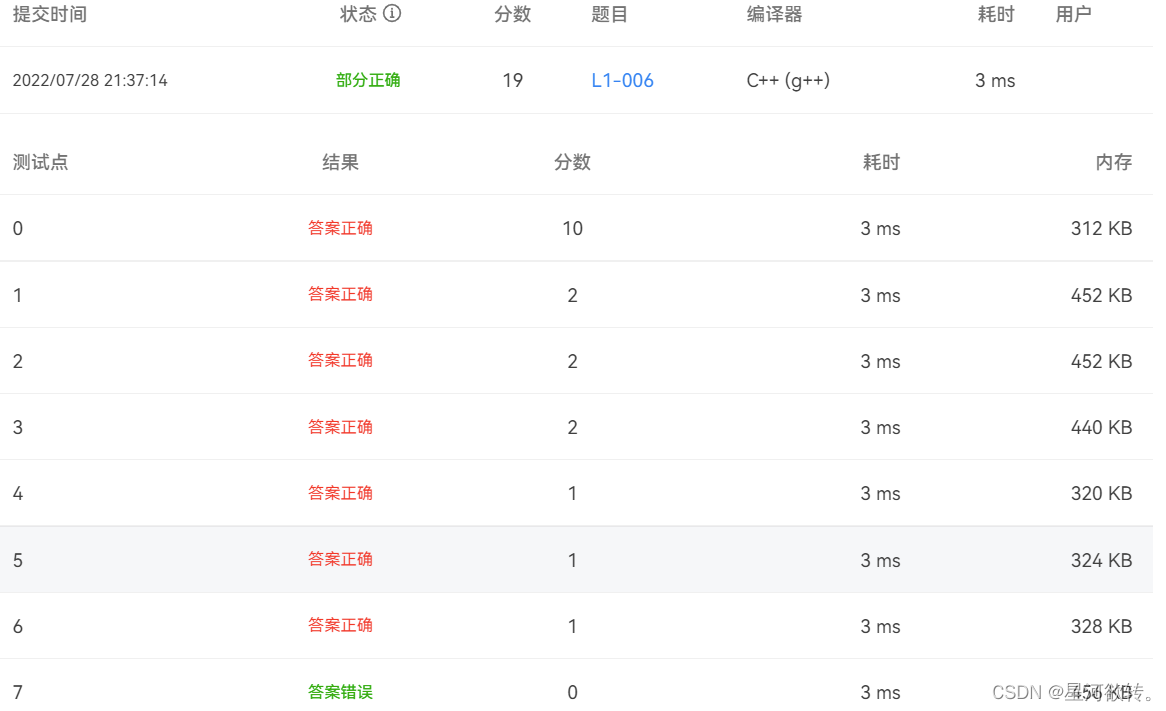
5*6*7

 //此题以前只有七个测试点，后又增加一个，导致无法满分，代码一为19分的代码，新增测试点可以这样理解，对于以前的测试点，当我们输入6的时候，测试结果为1换行2，但是应该为2换行2和3，出现这样的原因是，对6开根，只能取到2，但是3也是6的因子，并且2*3连续同时也是6的因子，sqrt向下取整，所以我们应该sqrt(n)+1,即可通过该测试点

 

//代码一 

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,x,d=0,i,j,a=1;
    cin>>n;
    x=n;
    for(i=2;i<=sqrt(n);i++){
        if(n%i!=0) continue;
        a=1;
        for(j=i;j<=sqrt(n);j++){
            a*=j;
            if(n%a!=0||a>n) break;
         }
         if(j-i>d){
             d=j-i;
             x=i;
         }
    }
    if(!d) d=1;
    cout<<d<<endl<<x;
    d+=x;
    for(i=++x;i<d;i++){
        cout<<"*"<<i;
    }
    cout<<endl;
    return 0;
}

//AC代码

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,x,d=0,i,j,a=1;
    cin>>n;
    x=n;
    for(i=2;i<=sqrt(n)+1;i++){
        if(n%i!=0) continue;
        a=1;
        for(j=i;j<=sqrt(n)+1;j++){
            a*=j;
            if(n%a!=0||a>n) break;
         }
         if(j-i>d){
             d=j-i;
             x=i;
         }
    }
    if(!d) d=1;
    cout<<d<<endl<<x;
    d+=x;
    for(i=++x;i<d;i++){
        cout<<"*"<<i;
    }
    cout<<endl;
    return 0;
}

//这里需要注意，d开始为0，如果最后判定d为0，d=1（比如输入3，然后输出1换行3），我最近犯了一个错误，就是d开始为1，那么就会导致输入4的时候，输出的是1换行4，但实际应该输出1换行2，如果(j-i)>d这里的判断加上等号，倒是可以符合实际输出，但是势必会影响最小的连续因子序列。题目要求是最长的、最小的连续因子，抓住这个重点。