计算机组织与结构【5 整数运算】

图片来源：南京大学软件学院COA课程PPT

©author:zzb

Github主页 优快云主页

5 整数运算

异或门是不能多个一起输入的，只能两两。a⊕b = (¬a ∧ b) ∨ (a ∧¬b)，由此推断，非门的门延迟也为1ty

而与和或则可以多个一起输入，因为如或门，只要有一个1 ，那么结果就是1，与门，只要有一个0，那么结果都是0

串行进位加法器

之所以s=x⊕y⊕c，把x和y先做异或，是为了节省时间，因为c需要由前面的数据得到，如上，C_n的延迟是2n ty，因此可以提前把x_n⊕y_n计算好，等C_n-1计算好后再和C_n-1异或，因此Sn的延迟为2(n-1)+3=2n+1

（但第一和第二位除外，它们的延迟都是6，因为得到C₁为2，而此时X₂和Y₃还没有异或就绪，所以仍然是S₂的延迟仍是6。C₂的延迟是4>3，因此X₃和Y₃已经异或完成，在等C₂）

（所有的A_i和B_i是同时输入的，等到C_i-1到来时，除了最低2位，A_i和B_i已经通过了异或门，因此这个3ty的时间延迟不算，而只用考虑与C_i-1的异或）

全先行进位加法器

把C都换掉代入，形成这些式子

C_i-1=1，P_i=1则表示能把这个C_i-1的1传递到C_i

只有X_i和Y_i都是1，G_i才为1，G_i表示这位能不能自己生成1

第一步把P和G都计算出，需要1ty

第二步根据式子把C全部计算出，因为式子中只有与和或，因此与可以一起进行，或可以一起进行，所以只要2ty

在第一步和第二步进行的过程中，同时在进行第三步X⊕Y，刚好3ty，因此第一第二和第三步是同时进行的

所以第四步就是进行（X⊕Y）⊕C计算出S，需要3ty

因此总共需要1+2+3=6ty

部分先行进位加法器

每8位用CLA（全先行进位加法器），整体用串行进位加法器，在时间和空间内得到平衡

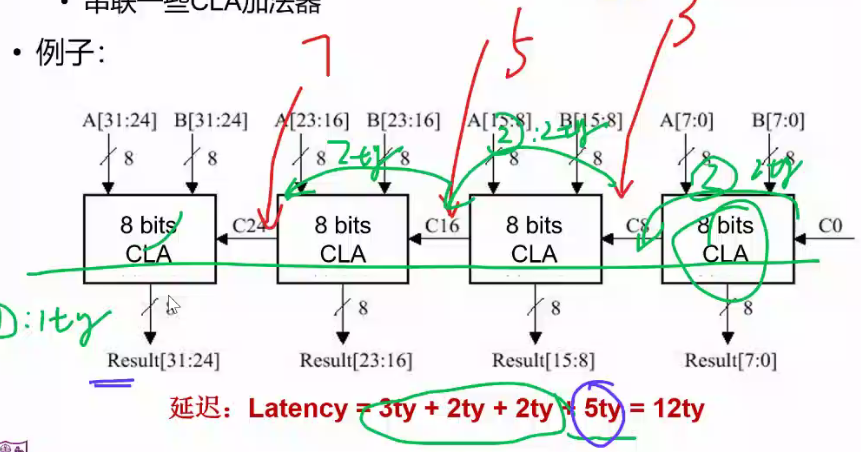
最后的5是=2+3，第4个CLA要进行第二步2ty和第四步3ty，所以是5ty，当最后一个计算完成时，前面的已经计算完了，所以全部计算好了

两个数加的补码是两个数补码的和

溢出的两种判定：

1. 加数符号相同而和不同（若符号不同不可能溢出）
2. Cn异或Cn-1

减法

乘法

计算机只能进行两两相加，因此每一步都把部分积求和

如下图，参与运算的是红色的部分，通过右移保证高4位是参与运算的

刚开始积为n为0，在乘的过程中，部分积的长度会慢慢变长，最终变成2n

但这样的话，2n位的右边n位会空着，会产生浪费，因此把右边n位用来存放乘数Y，这样Y的一位乘完后，右移空出来的位置就可以给积用，如上图，左边一半是乘积寄存器，右边一半是乘数寄存器

加了之后再右移

上面的乘法只适用于原码。

补码不能用于乘法，要用原码去乘，再把积用补码表示，但这样很麻烦，会消耗大量的计算资源。

因此出现了布斯乘法，可以用于补码的乘法

布斯乘法

在第四行中，为了保证式子的统一性，引入Y₀=0

2的-1次方即右移一位，与原来的乘法不同的地方就在绿色框中，原来是Y_i+1，现在是Y_i-Y_i+1（i从0开始，Y₀=0），这样，就可以适用于补码的乘法运算了

因为是Y_i-Y_i+1，相比于原来多了一种可能性**+X，-X，+0**

一共n位，所以要进行n次

因为这里可以处理补码整数，所以会出现负数的情况，如果右移补零那么会无论乘数如何，最后符号位总是0，即总是正数。而对于原来只能处理原码的情况，是不会出现负数的，因此始终是补零

因此在布斯乘法用于处理补码整数乘法时，右移应当是算术右移，符号拓展

除法

补充符号位直到除数最高位和余数的次高位对齐

因此即拓展除数位数长度的符号

要把4位的被除数符号拓展成8位，因为最终结果商应当是4位的

余数实际上是2n位，但只有低n位有用，因此余数只取低n位

恢复余数除法

实际上只有n位参与运算，但为了实现移位操作，用了2n位，因此造成了浪费，同样可以类比乘法来充分利用空间

把除数右移的操作，改成了余数左移的操作，左移右边空出来的就作为商，这样余数同样也只要四位即可

判断够不够减，是根据余数的左边四位来比较的

• 余数减去除数后，余数符号不发生改变，那么就是够减的
• 要使得余数的绝对值不断变小，并且符号不改变

最后如果除数和被除数的符号不同，那么要将商变成相反数，即取反加一

没有办法事先去判断够不够减，因此只能运算后看符号有没有变，因此对于机器来说，尝试运算后，发现不够减，那么要恢复余数

当商为4位时，达到所需精度，就运算完成，留下了余数

• 有没有可能左移的过程中符号变号了，如果有，那么余数的符号到底应该以那个为准**?**

• 我认为不会移出，如32位cpu中，除数和被除数都是32位，为了得到32位的商，应当把32位被除数符号拓展成64位，而总共运算n=32次，因此不会移出符号位，因此在这个过程中，符号一定不会发生改变，因此发生改变说明不够减，那么需要恢复

不恢复余数的除法

类似开车，当车偏离直线时，不会退回去变成直线，而是往右偏来纠正

• 乘2是左移
• 这里的余数R_i是不论是否够减了，都减去Y得到的
• 只考虑减法（当然有可能是加法，余数和除数异号时）：
  • 如果不够减，不需要在上一步进行恢复，而是在下一步通过加Y来同时实现上一步的恢复和这一步的减Y

---

第一次没有左移，是多一位商放在后面

然后再看余数和除数符号是否相同

同样运算n次

最后还需要对整除可能出现的问题进行判断（原因是如果发生整除，0的符号是0，会产生错误的判断）：

• 如果余数+除数=0，说明多减去一个除数，所以商要-1，余数置0
• 如果余数=除数，说明少减去一个除数，所以商要+1，余数置0

原码加减法理解

1. 特点：

   • 符号位不作为数的一部分参与运算
   • 符号位和加减法指令共同作为运算的依据

2. 规则

   • 加法指令：同号求和，异号求差
   • 减法指令：异号求和，同号求差

3. 对于求和：

   • 两个操作数相加得到的数值位，如果数值位最高位产生进位，则结果溢出
   • 若不溢出，则和的符号位采用第一操作数的符号

4. 对于求差：第一操作数的数值位加上第二操作数数值位的补码

   • 最高数值位有进位，表明加法结果为正，结果符号位采用第一操作数的符号

   • 最高数值位没有进位，表明结果为负（补码形式），应对结果求补码，还原成原码形式，结果的符号位为第一操作数的符号取反

   • 理解：事实上，是通过加模再减模（2^k）的方式把减法转成加法，因此如果加后最高位有进位，那么结果减去模就仍然是正数，那么直接取n位结果即可，最高位的进位截断（或者理解为减去了模，因此这个1被减去了）

     如果没有进位，那么说明结果减去模是负数，那么res-2^k就不够减，那么就提个负号出来变成-(2^k-res)，括号里面自然就是取反加1，同时外面的负号用于把第一操作数的符号位取反

为负（补码形式），应对结果求补码，还原成原码形式，结果的符号位为第一操作数的符号取反

• 理解：事实上，是通过加模再减模（2^k）的方式把减法转成加法，因此如果加后最高位有进位，那么结果减去模就仍然是正数，那么直接取n位结果即可，最高位的进位截断（或者理解为减去了模，因此这个1被减去了）

  如果没有进位，那么说明结果减去模是负数，那么res-2^k就不够减，那么就提个负号出来变成-(2^k-res)，括号里面自然就是取反加1，同时外面的负号用于把第一操作数的符号位取反