原文:Not all edges are peers: Accurate structure-aware graph pooling networks
摘要
图神经网络 (GNN) 在图相关任务中取得了最先进的性能。对于图分类任务,精心设计的池化算子对于学习图级表示至关重要。大多数源自现有 GNN 的池化算子通过对节点进行排序并选择一些排名靠前的节点来生成粗图。然而,这些方法未能探索图中节点以外的基本元素,这可能无法有效地利用结构信息。此外,所有连接到低排名节点的边都被丢弃,这破坏了图的连通性并丢失了信息。此外,所选节点倾向于集中在某些子结构上,而忽略其他子结构中的信息。为了应对这些挑战,我们提出了一种新的池化算子,称为精确结构感知图池化 (ASPool),它可以集成到各种 GNN 中以学习图级表示。具体来说,ASPool 自适应地保留边的子集来校准图结构并学习抽象表示,其中所有边都被视为非对等点,而不是简单地连接节点。为了保持图的连通性,我们进一步介绍了考虑排名靠前的节点和丢弃边的选择策略。此外,ASPool 执行两阶段计算过程,以保证采样节点分布在整个图中。在 9 个广泛使用的基准上的实验结果表明,与最先进的图形表示学习方法相比,ASPool 实现了卓越的性能。
1. 引言
众所周知,图可以对现实世界中普遍存在的复杂关系进行建模。与传统的网格数据不同,图结构数据在其图结构中拥有丰富的信息。近年来,人们对分析此类数据的兴趣日益浓厚。具体来说,已经开发了图神经网络 (GNN) 以推进跨不同领域的图学习(Galushka 等人,2021;Manco、Ritacco 和 Barbieri,2021 年;Valenchon 和 Coates;Wang 等人,2019 年;Zheng 等人。 , 2021) 并在各种与图相关的任务中取得了最先进的结果,例如图分类 (Gao, Liu, & Ji, 2021; Gao, Xiong, & Frossard, 2019; Ying et al., 2018) 、节点分类 (Kipf & Welling, 2017; Velickovic et al., 2018) 和链接预测 (Qu, Bengio, & Tang, 2019)。他们的成功依赖于消息传递原理,该原理通过沿图内的边进行转换、传播来整合拓扑结构和节点特征中的信息。在本文中,我们专注于图分类的图级表示学习。
对于图分类,我们的目标是预测任何给定图结构样本的标签;因此,需要图形级别的表示。一种简单的方法是全局集成由 GNN 算法获得的节点表示,例如最大/均值池移位(Hamilton, Ying, & Leskovec, 2017)。此类操作无法识别图中的子结构组。与此同时,忽略了层次信息,这对于预测图的属性可能至关重要。已经有一些尝试克服上述缺点(Gao & Ji, 2019; Lee, Lee, & Kang, 2019; Zhang et al., 2019),统称为分层图池化方法。上述工作主要分为两类。基于抽样的方法(Ranjan, Sanyal, & Talukdar, 2020; Zhang, Cui, Neumann, & Chen, 2018)按照定义的标准识别重要节点,然后对排名靠前的节点进行抽样以构建递归诱导子图(指定图中的一组点为初始点,并找出两个端点均为这些初始点的所有边,这些初始点和找到的边就构成了一张诱导子图,就是重要节点的边)。对于基于聚类的方法(Ying et al., 2018; Yuan & Ji, 2020),粗化图中的每个节点都是由代表输入图中的一组节点和边的聚合集群生成的。然而,这些池化操作仍有改进的空间。节点采样方法无法保留必要的子结构并在移除低排名节点时导致性能损失。节点聚类方法需要辅助网络来学习节点映射关系,存在高复杂度和过拟合问题。此外,上述方法从“节点”的角度引入更粗略的子图,而忽略了边在池化过程中的关键作用。
为了减轻上述限制,已经有一些初步尝试从“边缘”的角度设计池化算子。 EdgePool (Diehl, 2019) 计算边缘分数并连续合并由高分边缘链接的节点; EdgeCUT (Galland & Lelarge, 2021) 切割信息量较少的边,并将图分割成几个连接的组件,表示粗化级别的超节点。尽管利用边缘视图来设计池化算子,但它仍然没有得到有效使用:(1)目前不存在联合利用图中两个基本元素的池化算子。边和节点是图不可或缺的组成部分。直观地说,从“节点”和“边缘”的角度来看,派生的池化算子可能更实用。 (2) 在池化过程中,所有连接到低排名节点的边都被丢弃,这破坏了输入图的连通性,被移除的边中包含的有价值信息也消失了。 (3) 现有的池化算子没有考虑全局重要性和局部代表性来对图中的节点进行排序。限制是所选节点倾向于冗余地集中在某些子结构上,而忽略其他子结构中的信息。
在这项工作中,我们提出了一个新的池算子ASPool来学习层次化的图级表示。我们认为,边的作用不能简单地定义为连接节点,它们在图中不是对等的。具体来说,ASPool自适应地保留边缘的子集来校准图结构,并学习局部结构的抽象表示。此外,我们进一步引入同时考虑顶级节点和下降边的选择策略,以保持图的连通性,减少信息丢失。此外,ASPool执行两个阶段的计算过程,以保证抽样的节点分布在整个图中。主要贡献可概括如下:
- 引入了一种新颖的图池化算子 ASPool,以从“节点”和“边”的角度执行分层图表示学习,并且可以轻松集成到现有的 GNN 中。
- 据我们所知,我们是第一个提出不输入图中的所有边都是对等的,并在池化过程中区分和利用这些边,而不是直接删除一些边。•
- 我们在 9 个广泛使用的基准上评估 ASPool。实验结果清楚地表明,与其他最先进的图表示学习方法相比,ASPool 实现了卓越的图分类性能

据此引言部分结束,作者说了怎么多,就是想说他们的模型将边的参数进行了学习,从而提升模型的效果。
2. 相关工作
GNN 的研究将卷积神经网络 (CNN) (Krizhevsky, Sutskever, & Hinton, 2012) 的卷积和池化操作推广到图结构数据。现有的 GNN 设计了各种卷积算子,通过提取底层拓扑结构信息来学习低维表示。这些模型主要可以分为光谱方法(Bruna, Zaremba, Szlam, & LeCun, 2014; Defferrard, Bresson, & Vandergheynst, 2016; Li, Wang, Zhu, & Huang, 2018)和空间方法(Jin et al., 2021;Kim & Oh,2021;Wang 等人,2020)。有关 GNN 上卷积算子的更多详细信息,请参阅调查(Liu 等人,2021;Wu 等人,2021;Zhu 等人,2021)。在这里,我们专注于用于学习图级表示的池化算子。现有的图池化算子可以简单分为全局池化和分层池化。
全局池化模型采用对所有节点嵌入的全局汇总,形成抽象表示,然后执行任务。例如,Set2Set (Vinyals, Bengio, & Kudlur, 2016) 通过 LSTM (Torterolo & Garbay, 1998) 网络迭代地聚合信息来制定节点的重要性分数。 DCGNN (Li, Tarlow, Brockschmidt, & Zemel, 2016) 根据特征图值的最后一个通道输出具有固定大小的排序图表示。虽然灵活且直接,但这些琐碎的操作可能会丢失重要特征并忽略一些结构信息。
分层池化模型在每个节点级聚合之后执行池化操作,生成越来越粗略的图,然后执行任务。它们可以大致分为基于聚类的方法和基于抽样的方法。 DiffPool (Ying et al., 2018) 和 StructPool (Yuan & Ji, 2020) 附加到基于集群的方法,学习集群分配矩阵以将节点映射到一组集群。粗化图的连接模式可能与原始图有很大不同。最大的困难是它们庞大的计算成本很高。 U-Nets (Gao & Ji, 2019)、SAGPool (Lee et al., 2019)、HGP-SL (Zhang et al., 2019) 和 TAP (Gao et al., 2021),它们与采样有关-基于方法,通过设计节点选择标准来挑选出 k 个重要节点以形成诱导子图。这样的方法,涉及轻量级的额外参数,更有效且远非过度拟合。
值得注意的是,ASAP(Ranjan 等人,2020)通过在保持稀疏性的同时聚合所有相邻节点来学习本地集群的表示。它在多个基准测试中取得了最先进的性能。然而,我们认为集群嵌入不应该直接聚合所有邻域节点,而是它们的一个子集。 EdgePool(Diehl,2019)首先引入了基于边缘的收缩池化算子。它根据计算的边缘分数连续合并由最高分数的边缘链接的节点对。 EdgeCut (Galland & Lelarge, 2021) 计算边缘分数依赖于最小化 minCUT (Stoer & Wagner, 1997) 问题。它删除信息量较少的边,并将图拆分为几个表示超级节点的连接组件。这两种方法初步解释了边在图中的重要性。虽然边缘视图用于设计池化算子,但仍未得到有效使用。
我们提出的 ASPool 具有分层池的所有理想属性,可有效学习高级图表示。请参阅表 1 了解不同层次池化方法的总体比较。 ASPool 动态计算每条边的重要性分数,以确定要组合成集群的邻居中的节点子集。此外,它使用两阶段投票和额外策略明确保留了更重要的节点。
基本上到这里相关工作部分就结束了,这里就说一点,文章中提到的粗图,我个人理解的就是经过聚合之后的图嵌入表示。
3. 符号和问题陈述
我们将输入图 G 表示为 ( V , E ) G表示为 (V, E) G表示为(V,E),其中集合 V V V 包含所有节点,每个 e ∈ E e∈E e∈E代表节点之间的一条边。图结构可以用邻接矩阵 A ∈ R n × n A∈R^{n×n} A∈Rn×n表示,如果在 v i 和 v j v_i 和 v_j vi和vj之间存在边,则条目 A i j = 1 A_{ij}=1 Aij=1。 X ∈ R n × d X∈R^{n×d} X∈Rn×d 为节点特征矩阵, d d d为节点特征维数。每个图都与一个标签 y y y相关联,表示它所属的类,即 G G G属于类 j j j,则 y = 1 y=1 y=1,否则 y = 0 y = 0 y=0。
3.1 问题
给定一组图 G = { G ( 1 ) , G ( 2 ) , . . . , G ( m ) } \mathbb G = \{G^{(1)}, G^{(2)}, . . . , G^{(m)}\} G={G(1),G(2),...,G(m)} 及其对应的标签信息 Y = { y ( 1 ) , y ( 2 ) , . . . , y ( m ) } Y = \{y^{(1)}, y^{(2)}, . . . , y^{(m)}\} Y={y(1),y(2),...,y(m)},图分类的目标是学习一个映射函数 f m : G → Y f_m : \mathbb G →\mathbb Y fm:G→Y 来预测训练集中未见图的标签。池化图由 G p ( V p , E p ) G^p(V^p, E^p) Gp(Vp,Ep) 表示,其中节点嵌入矩阵为 X p X^p Xp,邻接矩阵为 A p A^p Ap。
要是读了原文的小伙伴,就会发现我修改了这图的标签。原文那个标注有问题,我感觉作者应该是没有注意到这个细节。无伤大雅。
3.2 对等点
描述输入图中所有边的作用,也就是说,仅连接第k层的成对节点。在这种情况下,所有的边都被不加区别地利用,我们称这些边为“对等点”。在这里,我们认为不是所有的边都是对等的;有些直接连接节点对,而另一些则连接两个抽象子图。
这是作者提出的一个新的概念,大家也不要太纠结这边的翻译是不是专业的。
4. 方法
4.1 整体架构
ASPool框架的总体视图如图1所示,这是一个层次化的GNN模型。具体来说,ASPool模块被堆叠在一个GCN模块上,这个过程会重复几次。GCN模块旨在学习有用的节点嵌入,而ASPool模块寻求生成粗化图作为下一层的输入。我们将GCN模块和池化模块的组合描述为一个学习块。然后,在学习块后面有一个读出函数来集成所有保留的节点表示,以输出相应的高级表示。最后的图级表示总结了不同层上的所有表示。并通过多层感知器(MLP)层来执行图的分类任务。整个体系结构可以通过端到端方式进行优化。与现有的池化方法不同,ASPool在数据驱动下自适应地保留了图的基本元素(节点和边),以获取有价值的信息。另一方面定义节点选择标准,保证保留节点在整个图中的分布。我们将提出的框架称为精确结构感知图池网络(ASPool)。
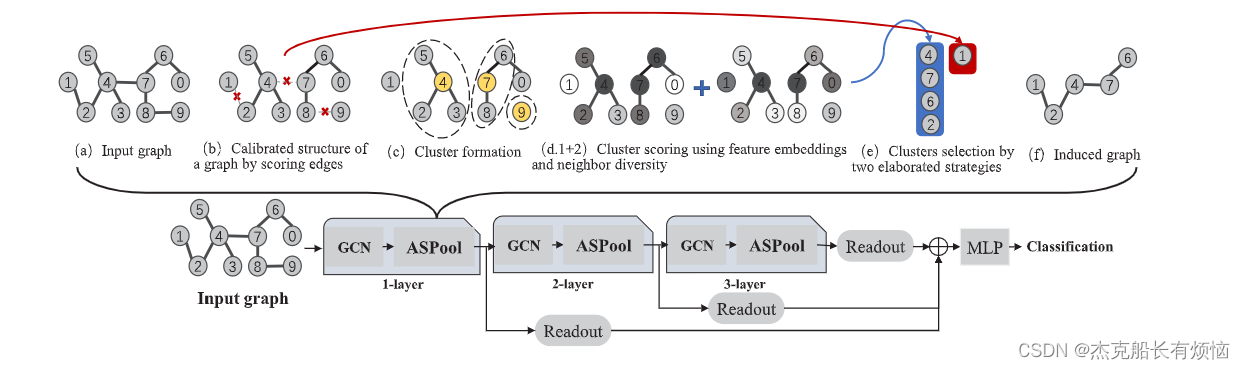
4.2 图卷积网络
大多数 GNN 遵循消息传播机制,利用特征和结构信息来学习节点表示。具体来说,GNN 的每一层首先聚合来自 k-hop 邻居 N k ( v ) N_k(v) Nk(v)的信息,然后通过特征变换更新节点表示。已经提出了几种特征聚合函数。最具代表性的方法之一是图卷积网络 (GCN) (Kipf & Welling, 2017)。它由几个卷积层组成,GCN的第 l l l层可以表示如下:

上面公式的定义就和GCN里面的一样,要是不明白可以看看关于GCN的文章
4.3 图池化操作
受到ASAP (Ranjan et al., 2020)的启发,ASPool最初还考虑给定输入图的所有可能的本地集群,帮助捕获图子结构中存在的信息。然而,我们认为不是所有的边都是对等的;有些直接连接节点对,而另一些连接两个抽象组(子图)。相应地,应该以不同的方式利用边缘,而不是在一次操作中直接删除或保留。此外,图的校准结构和节点被综合利用来解决1中引入的挑战-(1)。((1)目前不存在联合利用图中两个基本元素的池化算子。边和节点是图不可或缺的组成部分。直观地说,从“节点”和“边缘”的角度来看,派生的池化算子可能更实用。)
4.3.1 通过评分边来校准图的结构
ASPool 不会合并所有相关节点来生成集群的表示。它首先引入了一个名为边缘信息分数的标准来评估每个边缘包含的信息,用于执行边缘采样。通常,边的重要性取决于两个连接的节点。我们将边缘信息分数 ϕ e i \phi_{e_i} ϕei 正式定义为函数 F e d g e s ( x i k , x j k ) F_{edges}(x^k_i , x^k_j ) Fedges(xik,xjk),具体实现如下:

其中 a ⃗ ∈ R 1 × d , W ∈ R d × 2 d \vec a∈R^{1×d}, W ∈ R^{d×2d} a∈R1×d,W∈Rd×2d 分别是可学习向量, x i k , x j k x^k_i , x^k_j xik,xjk 是第 k k k 层由一条边连接的节点的特征, σ σ σ 是激活函数。边缘信息分数 Φ e d g e s = [ Φ e 1 , Φ e 2 , . . . , Φ e m ] Φ_{edges}=[\mathcal\Phi_{e_1},\mathcal\Phi_{e_2} , . . . ,\mathcal\Phi_{e_m} ] Φedges=[Φe1,Φe2,...,Φem],我们可以选择与节点连接的边和在高级学习中起作用的边。接下来,我们执行边缘保留以根据定义的边缘池化比率 r e d g e a s r_{edgeas} redgeas 来校准输入图的拓扑结构,如下所示:
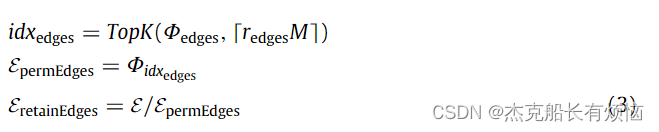
其中 M M M为边数; T o p K ( ⋅ ) TopK(\cdot) TopK(⋅)对边缘评分进行排序,给出top的索引 ⌈ r e d g e s M ⌉ ⌈redgesM⌉ ⌈redgesM⌉;符号 ′ / ′ '/' ′/′表示删除操作。 E p e r m E d g e s E_{permEdges} EpermEdges包含连接该层中节点的所有边, E r e t a i n E d g e s E_{retainEdges} EretainEdges是所有剩余的边。在这里,我们得到了校正图 G ′ = ( V , E p e r m E d g e s ) G ' = (V, E_{permEdges}) G′=(V,EpermEdges)。
这里作者的一番操作,我简直就是看蒙了。我还是太年轻了,完全看不懂作者想干什么。但是看了几遍后我就懂了。上面的F打分函数是为了r这个比率来服务的,然后取出这个比率最大的前k个,将其对应的permedges取出来。最终得到G‘
4.3.2 集群的形成
我们将每个节点 v i v_i vi 定义为集群 c k ( v i ) c_k(v_i) ck(vi) 的中心,使得每个集群表示 k k k 跳的固定半径内的本地邻居 N N N,即 c k ( v i ) = N k ( v i ) c_k(v_i) = N_k(v_i) ck(vi)=Nk(vi)。令 x c i 为 c k ( v i ) x_{c_i}为c_k(v_i) xci为ck(vi) 的特征表示。这里的任务是通过关注$ G’$ 中与 v i v_i vi 相关的节点来学习 c k ( v i ) c_k(v_i) ck(vi) 的表示。我们采用自注意力机制结合节点特征来学习集群表示 x i c x^c_i xic 。关键参数 m i ∈ R d m_i ∈ \R^d mi∈Rd 由 max 函数创建,它代表所有相关节点。它使用附加注意处理所有组成节点 v j ∈ c k ( v i ) v_j ∈ c_k(v_i) vj∈ck(vi),如下所示:

其中 x j ′ x'_j xj′ 是通过 GCN 模块传递 x j x_j xj 获得的, w ⃗ 1 T 和 W 1 \vec w^T_1和W_1 w1T和W1 分别是可学习的向量和矩阵。计算出的注意力分数 α i , j α_{i,j} αi,j 表示节点 v j 在 c k ( v i ) v_j在c_k(v_i) vj在ck(vi) 的成员强度。此外,在生成集群表示时应考虑中心节点的特征。这是因为图中的每个节点具有不同的重要性,一些节点位于图的远程位置,仅连接到几个节点。在这项工作中,我们采用中心节点的特征和度数以及集成的邻居表示来共同生成集群表示,其定义如下:

其中超参数β,w则是可学习向量。
4.3.3 通过两阶段程序进行聚类评分
与 Top-k (Gao & Ji, 2019) 类似,我们对一小部分簇进行采样。直观地说,应该保留极大地反映输入图的子结构的集群。此外,选择的节点/簇应该分布在整个图中,而不是集中在一些子结构上,这解决了 1 中引入的挑战-(3)。((3) 现有的池化算子没有考虑全局重要性和局部代表性来对图中的节点进行排序。限制是所选节点倾向于冗余地集中在某些子结构上,而忽略其他子结构中的信息。)为此,我们定义了一个函数 F c l u s t e r s F_{clusters} Fclusters来计算重要性分数 Φ c l u s t e r s Φ_{clusters} Φclusters 通过两个阶段程序如下:

其中第一项:p是个可学习的投影向量,用来调整 x i c x^c_i xic;通过添加第二项来解决局部的代表性,第二项反映了两个连接集群的表示之间的关系。当节点 v i v_i vi的集群表示与位于同一局部子结构中的其他节点 v j v_j vj 的集群表示相似时,得到的计算量会很小,反之亦然。
4.3.4 通过精心设计的策略选择集群
这里我们得到了 Φ c l u s t e r s = [ F φ c l u s t e r 1 , F φ c l u s t e r 2 … F φ c l u s t e r N ] Φ_{clusters} = [F_{φ_{cluster1}},F_{φ_{cluster2}}…F_{φ_{clusterN}}] Φclusters=[Fφcluster1,Fφcluster2…FφclusterN]。值得注意的是,在上述图学习过程中使用了校正图 G ′ = ( V , E p e r m E d g e s ) G ' = (V, E_{permEdges}) G′=(V,EpermEdges)。连接两个抽象组的边保存在 E r e t a i n E d g e s E_{retainEdges} EretainEdges中。为了保持图的连通性并减少信息丢失((2) 在池化过程中,所有连接到低排名节点的边都被丢弃,这破坏了输入图的连通性,被移除的边中包含的有价值信息也消失了。)我们引入了同时考虑顶级节点和“丢弃”边的选择策略。我们首先根据计算出的 Φ Φ Φ和边缘池比率 r n o d e r_{node} rnode对集群进行排序如下:

为了保留 e r e t a i n e d g e e_{retainedge} eretainedge中覆盖的结构信息,我们需要进一步保留包含在 e r e t a i n e d g e e_{retainedge} eretainedge中的对应节点,(记作 v r e t a i n e d g e v_{retainedge} vretainedge)如下:

其中 ϕ \phi ϕ表示节点的重要性得分, γ γ γ是超参


4.4 读出函数和输出层
为了生成固定大小的图级表示,每个学习块的输出都汇总在读出层中。在这里,我们使用 Xu 等人提出的公式。 (2018)如下:


损失函数:交叉熵(多分类)
据此模型就介绍完毕了,总体来说确实设计的都很巧妙,推荐阅读是带着图来读这些公式,一步一步的看。但是复现这些的话,难度就很大了,基本上这篇文章大家可以当一个零件库,一个一个的取。主要的好处是,你要是用了这些零件,人家连介绍都给你想好了,直接用就行了。
5. 实验











 本文提出了一种新的图池化算子ASPool,用于图神经网络(GNN)中的图级表示学习。ASPool自适应地保留边的子集,以校准图结构并学习抽象表示,强调边在图中的非对等作用。它通过考虑节点和边的重要性来避免传统池化方法中信息丢失的问题,同时保持图的连通性。在9个基准数据集上的实验显示,ASPool在图分类任务上优于现有方法。
本文提出了一种新的图池化算子ASPool,用于图神经网络(GNN)中的图级表示学习。ASPool自适应地保留边的子集,以校准图结构并学习抽象表示,强调边在图中的非对等作用。它通过考虑节点和边的重要性来避免传统池化方法中信息丢失的问题,同时保持图的连通性。在9个基准数据集上的实验显示,ASPool在图分类任务上优于现有方法。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








