数据结构（二）凸包

凸包求解

【问题描述】
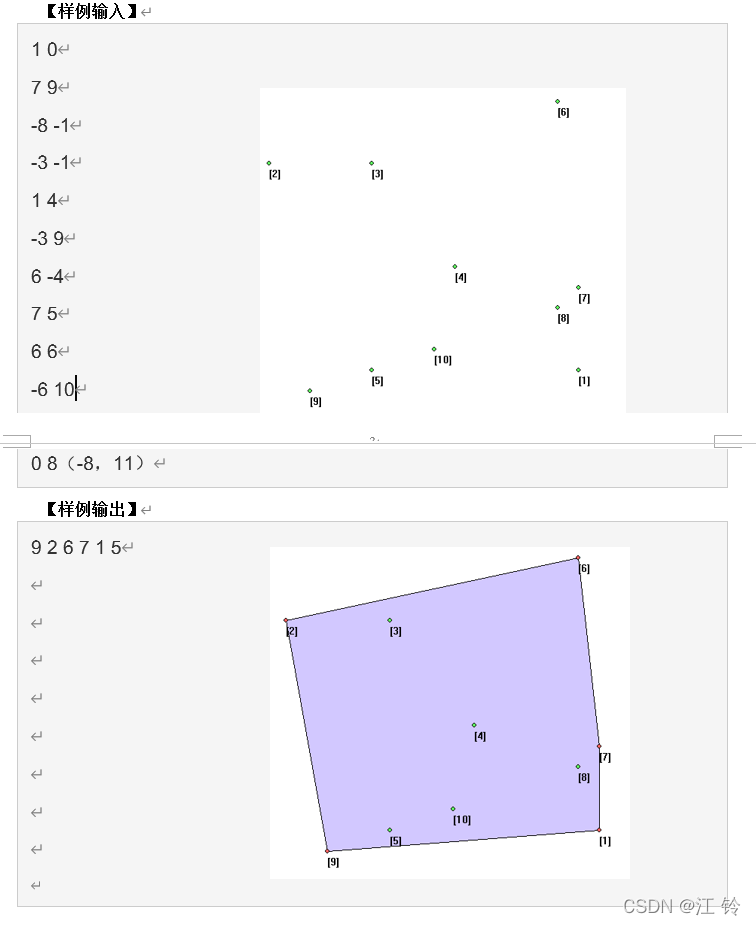
凸包是一种基础的几何结构，在地理信息科学领域广泛应用。给出一组平面上的点，构造出对应的凸包，并依次输出极点编号。
【输入格式】
第一行即输入点的总数n，接下来n行依次给出各点的横纵坐标，横坐标与纵坐标间用空格分隔，如样例所描述。
【输出格式】
依次输出各个极点的对应编号（编号从1开始，而非0）。
可基于界面编程将凸包可视化。要求算法代码和界面代码分离。

---

原理分析：

1. 找到所有点中纵坐标y最小的点，也就是这些点中最下面的点，记为p0。
2. 然后计算其余点与该点的连线与x轴之间夹角的余弦值，将这些点按其对于最低点的正弦值从大到小排序，排序好的点记为p1, p2, p3, …
3. 将最低点p0和排序好的点中的第一个点p1压入栈中，然后从p2开始计算，计算栈顶两个点与该点三点向量是否是逆时针转动，若是，则将该点压入栈中，否则将栈顶元素推出。（此处对栈的概念不清楚可自行搜索）
4. 最后栈里面元素就是所有的凸包外围的点
   判断是否为逆时针旋转
   area = (b.x-a.x) * (c.y-a.y) - (b.y-a.y) * (c.x-a.x)
   
   area >0，A-B-C逆时针旋转；
   area <0，A-B-C顺时针旋转；
   area =0，A-B-C在一条直线上。

---

核心代码部分（C++头文件如下）

#pragma once
#include<iostream>
#include<cmath>
#include<stack>
using namespace std;

struct ConPnt
{
	int x;
	int y;
	float coszhi;
	ConPnt(int xx = 0, int yy = 0, double cosV = 0)
	{
		x = xx;
		y = yy;
		coszhi = cosV;
	};
};

ConPnt* finalpoints;
ConPnt* rawpoint;
stack<ConPnt>resultpoint;
int Ptotal;

//复制函数
void copyConPnt() {
	memcpy(finalpoints, rawpoint, sizeof(struct ConPnt) * Ptotal);
}

//找到Y值最小的点
int SortY(ConPnt* points) {
	int  Min = 0;
	for (int i = 1; i < Ptotal; i++) {
		if (points[i].y < points[Min].y)
			Min = i;
		if (points[i].y == points[Min].y)
		{
			if (points[i].x < points[Min].x)
				Min = i;
		}
	}
	return Min;
}

//计算余弦值
void Calculate(ConPnt* points, int Min) {
	for (int i = 0; i < Ptotal; i++) {
		if (i == Min) {
			points[i].coszhi = 1;
		}
		else {
			//与X轴组成的直角三角形
			double xfang = pow((points[i].x - points[Min].x), 2);
			double yfang = pow((points[i].y - points[Min].y), 2);
			points[i].coszhi = (points[i].x - points[Min].x) / sqrt(xfang + yfang);
		}
	}
}

//按照cos值排序,使用选择排序
void sortpoint(ConPnt*points) {
	ConPnt temp;
	for (int i = 0; i < Ptotal; i++) {
		//max变量保存该趟比较过程中，最大元素所对应的索引，
		//先假设前面的元素为最大元素
		int maxIndex = i;
		/*每趟比较，将前面的元素与其后的元素逐个比较*/
		for (int j = i + 1; j < Ptotal; j++) {
			//如果后面的元素大，将后面元素的索引极为最大值的索引
			if (points[j].coszhi > points[maxIndex].coszhi) {
				maxIndex = j;
			}
			if (points[j].coszhi == points[maxIndex].coszhi) {
				if (points[j].x < points[maxIndex].x)
				{
					maxIndex = j;
				}
				if (points[j].x == points[maxIndex].x)
				{
					if (points[j].y > points[maxIndex].y)
					{
						maxIndex = j;
					}
				}
			}
		}
		//然后交换此次查找到的最大值和原始的最大值
		if (points[maxIndex].coszhi >= points[i].coszhi) {
			temp = points[i];
			points[i] = points[maxIndex];
			points[maxIndex] = temp;
		}
	}
	int a = 0;
}

/*判断是否为逆时针旋转
area = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x)
area > 0，A - B - C逆时针旋转；
area < 0，A - B - C顺时针旋转；
area = 0，A - B - C在一条直线上。*/
int Counterclockwise(ConPnt a,ConPnt b,ConPnt c) {
	int area = (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
	return area;
}

//一条直线上是同向还是异向
int tongyixiang(ConPnt a, ConPnt b, ConPnt c)
{
	int Direction = (b.x - a.x) * (c.x - a.x) + (b.y - a.y) * (c.y - a.y);
	return Direction;
}

//Graham扫描法
void Graham(ConPnt*points)
{
	resultpoint.push(points[0]);
	resultpoint.push(points[1]);
	for (int i = 2; i < Ptotal;)
	{
		ConPnt temp = resultpoint.top();
		resultpoint.pop();
		//若是在同一侧那么压到结果数组中
		if (Counterclockwise(resultpoint.top(), temp, points[i]) >0)
		{
			resultpoint.push(temp);
			resultpoint.push(points[i]);
			i++;
		}
		if (Counterclockwise(resultpoint.top(), temp, points[i]) == 0)
		{
			if (tongyixiang(resultpoint.top(), temp, points[i]) > 0)
			{
				resultpoint.push(temp);
				resultpoint.push(points[i]);
				i++;
			}
		}
	}
}

//判断是否重复
bool twice(ConPnt a, ConPnt b[],int m)
{
	for (int i = 0; i < m; i++)
	{
		if (a.x == b[i].x && a.y == b[i].y)
		{
			return true;
		}
	}
	return false;
}

void clearall()
{
	delete rawpoint;
	delete finalpoints;
	while (!resultpoint.empty()) 
	{
		resultpoint.pop();
	}
}

---

结果

见图片中的使用说明
点击restart可重新绘制

注意

使用参考中的思想会存在部分问题
1.点数过多会出现边界点连接顺序错误
2.一些与Y值最小点连线为同一线的不同点也会被连接
3.点击程序外，绘制的线条会消失（可能与QT的repaint函数有关）
已经在代码中进行了修改
1.增加判断连线若在一条线，同向还是异向
2.排序时按照cos值（若需要），Y值，X值的顺序
即，第一遍排Y值时若相同再比X值，第二遍若COS值相同，就比较Y值，Y值相同比较X值，可避免1,2问题

凸包算法(convex hull)
https://blog.youkuaiyun.com/qq_39747794/article/details/81563346?ops_request_misc=&request_id=&biz_id=102&utm_term=Convex%20Hull&utm_medium=distribute.pc_search_result.none-task-blog-2_blogsobaiduweb~default-4-81563346.nonecase&spm=1018.2226.3001.4450