并查集～～

并查集的定义

取自：Union、Find、Set
功能：
1、合并：合并两个集合
2、查找：判断两个元素是否在一个集合内
实现方式：数组

int father[N];

father[i]：表示i的父亲结点。
father[i] = i由于一个集合中只能有一个根结点，且将其作为所属集合的标识。

并查集的基本操作

1、初始化

for(int i = 1; i <= N; i++){
	father[i] = i;
}

2、查找
由于规定同一个集合中只能有一个根结点，所以查找操作就是对给定的结点寻找其根结点的过程。

int findFather(int x){
	while(x != father[x]){
		x = father[x];
	}
	return x;
}

也可以用递归实现哈～

int findFather(int x){
	if(x == father[x])	return x;
	else	return findFather(father[x]);
}

3、合并
判断两个元素，如果是不同集合，那就合并。一般来说，一个集合的根结点的父结点会指向另一个集合。

思路～
1、对于两个结点，先判断其根结点是否相同（可以调用上面的函数）。
2、合并两个集合：在1、中获取的两个集合的根结点faA和fbB，只需要把其中一个的父亲结点指向另一个结点就可以了。

代码如下～

void Union(int a, int b){
	int faA = findFather(a);
	int faB = findFather(b);
	if(faA != faB)
		father[faA] = faB;
}

并查集的一个性质：
在合并的过程中，只对两个不同的集合进行合并，如果两个元素在相同的集合中，那就不会对它们进行操作。这就保证了在同一个集合中一定不会产生画面，即并查集产生的每一个集合都是一棵树。

路径压缩

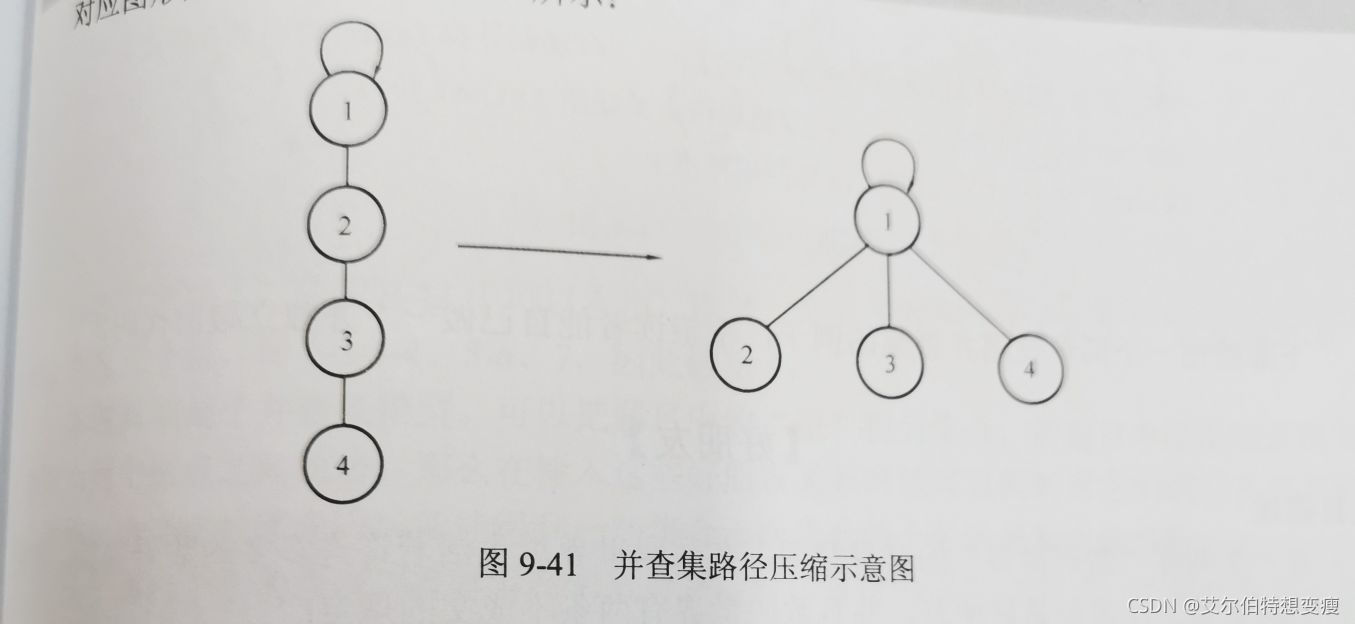
因为只需要寻找根结点，所以用上图的方法更快找到。O(1)
实现转换的步骤：
1、按照原先的方法获取x的根结点。
2、重新从x走一遍寻找根结点的过程，把路径上经过的所有结点的父亲结点全都改为根结点r
代码如下～

int findFather(int x){
	int a = x;
	while(x != father[x])
		x = father[x];
	
	while(a != father[a]){
		int z = a;
		a = father[a];
		father[z] = x;
	}
	return x;
}

以下为递归操作～

int findFather(int v){
	if(v == father[v]){
		return v;
	}else{
		int F = findFather(father[v]);
		father[v] = F;
		return F;
	}
}