基于相似度的方法

“异常”通常是一个主观的判断，需要结合业务背景和环境来具体分析确定。噪声和异常之间、正常数据和噪
声之间的边界都是模糊的。异常值通常具有更高的离群程度分数值，同时也更具有可解释性。

嵌套循环
第一层循环遍历每个数据，第二层循环进行异常判断，需要计算当前点与其他点的距离，一旦已识别出多于 个数据点与当前点的距离在 之内，则将该点自动标记为非异常值。这样计算的时间复杂度为 ，当数据量比较大时，这样计算是及不划算的。 因此，需要修剪方法以加快距离计算。

基于单元的方法
在基于单元格的技术中，数据空间被划分为单元格，单元格的宽度是阈值D和数据维数的函数。具体地说，每个维度被划分成宽度最多为 单元格。在给定的单元以及相邻的单元中存在的数据点满足某些特性，这些特性可以让数据被更有效的处理。

以二维情况为例，此时网格间的距离为 ，需要记住的一点是，网格单元的数量基于数据空间的分区，并且与数据点的数量无关。这是决定该方法在低维数据上的效率的重要因素，在这种情况下，网格单元的数量可能不多。 另一方面，此方法不适用于更高维度的数据。

基于索引的方法
对于一个给定数据集，基于索引的方法利用多维索引结构(如 树、 树)来搜索每个数据对象
在半径 范围 内的相邻点。设 是一个异常值在其 -邻域内允许含有对象的最多个数，若发现某
个数据对象 的 -邻域内出现 甚至更多个相邻点， 则判定对象 不是异常值。该算法时间复
杂度在最坏情况下为 其中 是数据集维数， 是数据集包含对象的个数。该算法在数据集
的维数增加时具有较好的扩展性，但是时间复杂度的估算仅考虑了搜索时间，而构造索引的任务本身就
需要密集复杂的计算量。

基于密度的度量
基于密度的算法主要有局部离群因子(LocalOutlierFactor,LOF)，以及LOCI、CLOF等基于LOF的改进算法

k-距离（k-distance§）：
对于数据集D中的某一个对象o，与其距离最近的k个相邻点的最远距离表示为k-distance§，定义
为给定点p和数据集D中对象o之间的距离d(p,o)，满足：
在集合D中至少有k个点 o’，其中 ，满足
在集合D中最多有k-1个点o’，其中 ，满足
直观一些理解，就是以对象o为中心，对数据集D中的所有点到o的距离进行排序，距离对象o第k近
的点p与o之间的距离就是k-距离。

k-邻域（k-distance neighborhood）：从“距离”这个概念延伸到“空间”

可达距离（reachability distance）：若 在对象o的k-邻域内，则可达距离就是给定点p关于对象o的k-距离；
若 在对象o的k-邻域外，则可达距离就是给定点p关于对象o的实际距离。

局部可达密度（local reachability density）：
我们可以将“密度”直观地理解为点的聚集程度，就是说，点与点之间距离越短，则密度越大。在这
里，我们使用数据集D中给定点p与对象o的k-邻域内所有点的可达距离平均值的倒数（注意，不是导
数）来定义局部可达密度。

局部异常因子：最终得出的LOF数值，就是我们所需要的离群点分数。在sklearn中有LocalOutlierFactor库，可以
直接调用。

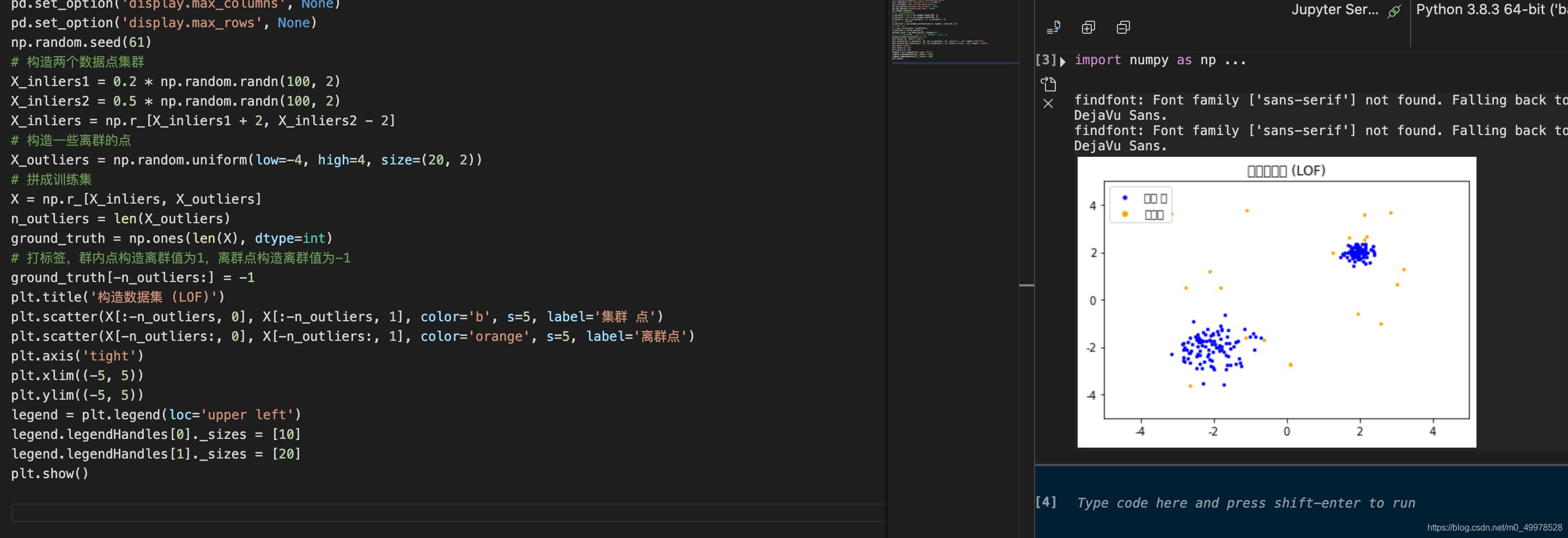
然后使用LocalOutlierFactor库对构造数据集进行训练，得到训练的标签和训练分数（局部离群值）。

将训练分数（离群程度）用圆直观地表示出来，并对构造标签与训练标签不一致的数据用不同颜色的圆进行标注。