LeetCode No.53 最大子序和 java 贪心 动态规划 (1)

---

题目

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。
示例1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [0]
输出：0

示例 4：

输入：nums = [-1]
输出：-1

示例 5：

输入：nums = [-100000]
输出：-100000

提示：
1 <= nums.length <= 3 * 104
-105 <= nums[i] <= 105

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

来源：力扣（LeetCode）
链接：LeetCode No.53 最大子序和

---

题解

本题有非常多的解法，我所知道的有：

1. 最暴力的相比较法（把所有子序列列出来然后比较他们的求和值）
2. 贪心算法
3. 动态规划
4. 分治算法

除了第一种方法，下面我们来分别研究每一种方法，本期我们来细说贪心算法和动态规划，明天我将补充上分治的写法。

贪心算法

贪心：在对问题求解时，总是做出在当前看来是最好的选择。而在这道题的体现中，贪心的核心思想是：当前所指元素以及之前的元素之和若小于0，则舍弃这一元素之前的所有数列。

这句话是什么意思呢？它是在说，我们从数组头开始遍历，走到一个元素时计算这个元素以及之前元素的和：

如果元素之和小于0，则舍弃这一段数组，从下一个元素再开始相加：

注意上述的 max = Math.max(-2, -2) 的意思是：max = Math.max(-2, -3 + 1)，是当前子串之和与之前的max值相比得出新的max值
接下来：

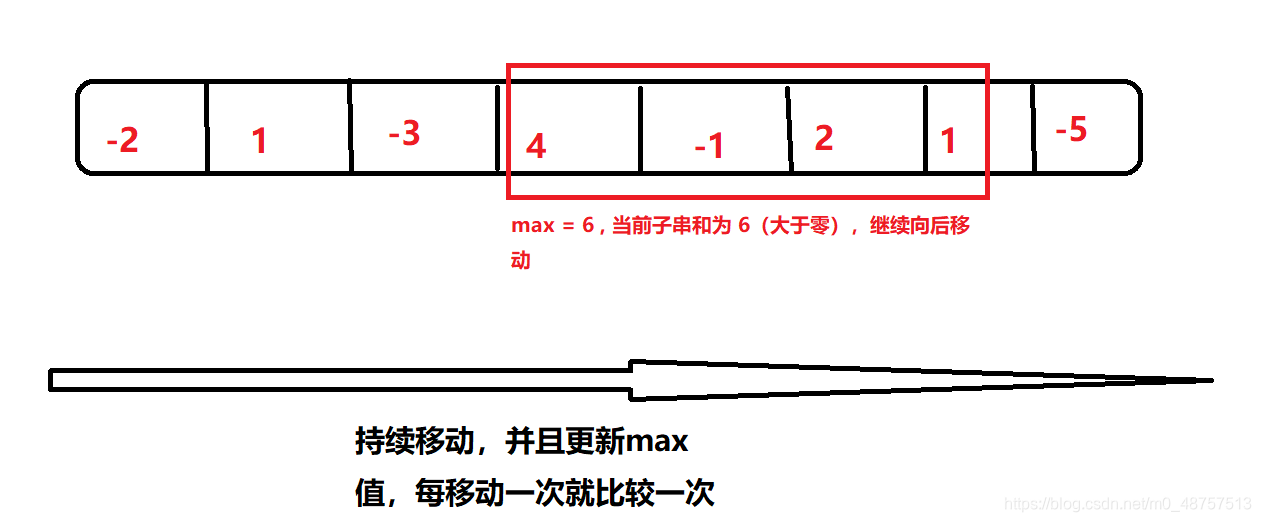
最后：

以上就是程序遍历的大致过程，以下我列出我觉得需要注意的点：

注意：

1、为什么是以小于0为判断依据？如果数组全为负数那岂不是全都跳过了？

解释：首先，小于零的话只要相加，值就会变小，而且越相加，值则越来越小。
而且不会全都跳过，因为每一次移动都与max值进行了比较，使max值一直都是最大的值，因此全都是负数的数组的答案会是数组中数值最大的那个负数。

2、让我理解本题的关键：

如果确认的最大子串，则相邻的子串之和一定是小于零的，不然大于零的话则最大子串就是这两个子串相并的子串了，所以利用反向思维，我们在判断到有小于零的子串的时候就舍弃这一段子串！

我的代码：

//贪心算法
class Solution{
    public int maxSubArray(int[] nums) {
        int max = Integer.MIN_VALUE, sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
            max = Math.max(max, sum);
            if (sum <= 0)
                sum = 0;
        }
        return max;
    }
}

执行结果如下：

令我惊奇的是，这个内存消耗真的惨目忍睹

---

动态规划（dp）

在我的认知中，dp方法往往让人惊叹，因为比较难想到，而且dp的效率也往往很高。

思路：
从数组头开始遍历，每遍历到一个数 i ，判断上一个数 j 是否为负数，为正数则 i = i + j（改变了i值），为负数则不用计算。

解释：
首先，若为负数不用计算，这个思路和上述贪心的“注意”里的思路一样，，为正数就加到该元素上，遍历完成后找整个数组的最大值即可，时间复杂度和空间复杂度都为O（n），但是空间复杂度可以优化至O（1）

dp解法1

执行图解：

程序初始化：

下一步：

然后到第三个数时，第二个数为正数，则进行相加：

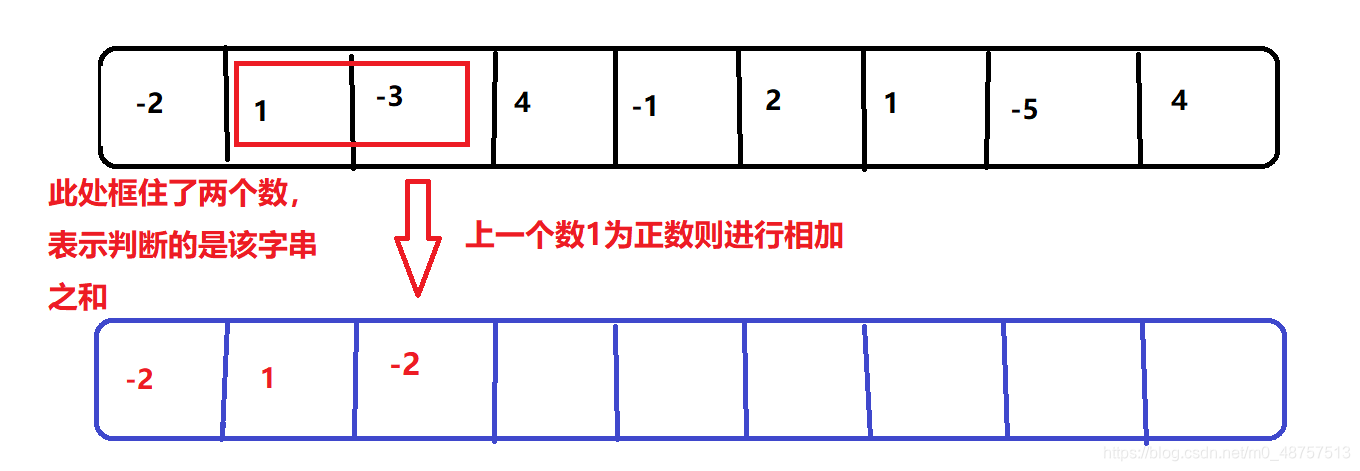
到这一步我们发现此处的值变为-2，成为负数了，因此抛弃前一段子串，进行新一轮子串的生成，之后的操作：

再之后就是重复的操作然后遍历出所有的值，遍历到最大子串时，子串最后一个数就是最大字串之和：

之后的虽然都是正数可以相加，但是值已经比最大字串值小：

核心思路和上述贪心的核心思路大同小异，只不过执行的方法不相同：都是要抛弃小于 0 的相邻子串，取最大的子串

dp解法2

该方法和dp解法1的思路是一样的，不过这一个流程优化了空间复杂度使其从O（n）变成了O（1），初始化max值和pre值，pre值用于记录子串之和，max用于记录所有子串之和中的最大值

然后，这一操作之后，相当于抛弃了之前的负数-2，开始了新的子串，同时更新了pre 和 max 值：

向后遍历之后，此时值pre值已为负数，因此在下一轮迭代中会被舍弃掉该串，从当前元素开始记录新的子串：

接下来的判断很关键：

接下来：

再往后的话，pre的值会更新，但是max的值已经不会更新了，到最后：

答案代码

class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0, maxAns = nums[0];
        for (int x : nums) {
            pre = Math.max(pre + x, x);
            maxAns = Math.max(maxAns, pre);
        }
        return maxAns;
    }
}

---

总结

以上就是今天要讲的内容，本文通过 LeetCode的第53题（最大子序和） 仅仅简单介绍了贪心算法和动态规划的使用，而这两种题目类型还有大量的变种题目，我会慢慢吸收各类变式题型来进行解答，附上今天随手拍的教学楼

希望大家能给个三连支持一下~