排序部分总结：

前言

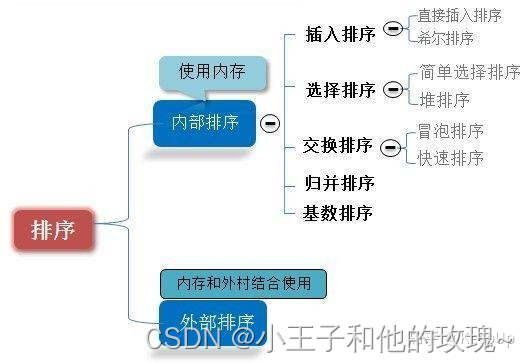
一、插入排序

1、直接插入排序

将一个记录插入到已经排好的有序序列中，从而得到一个新的记录数加一的有序表。
步骤：
1、取第一个元素，该元素可认为已经被排序
2、取出下一个元素key,与已经排序好的元素p从后向前相比较（因为是升序排列，故要比较最大的数）
3、如果该元素p（已排序）大于新元素key，将该元素p移到下一个位置；
4、重复步骤三，直到已排序的元素p小于新元素key,将新元素插入到p的后面。
5、重复步骤234
时间复杂度：
最差时间复杂度：O(n^2)
最优时间复杂度：O(n)
平均时间复杂度：O(n^2)
稳定性：稳定
%%%%%%%
例：
49 38 65 97 76
第一次：
49 和38比较 ，49后移—>38 49
38 49 65，key是65，大于49，所以不动 38 49 65
97同理
38 49 65 97 76----由于76小于97，97后移，65小于76，->38 49 65 76 97

void InsertionSort(int *a, int len)
{
	for (int j=1; j<len; j++)
	{
		int key = a[j];
		int i = j-1;
		while (i>=0 && a[i]>key)
		{
			a[i+1] = a[i];
			i--;
		}
		a[i+1] = key;
	}

2、希尔排序

希尔排序（Shell Sort），也称为递减增量排序算法，是插入排序的一种高速而稳定的改进版本。
基本思想：
先选定一个整数gap，把待排序文件中所有记录分成gap个组，所有距离为gap的记录分在同一组内，并对每一组内的元素进行排序。
然后将gap逐渐减小重复上述分组和排序的工作。
当到达gap=1时，所有元素在统一组内排好序。
希尔排序的特性总结：
希尔排序是对直接插入排序的优化。
当gap > 1时都是预排序，目的是让数组更接近于有序。当gap == 1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。
希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，这里不深究。
时间复杂度O(N^1.5)
空间复杂度O(1)
稳定性：不稳定。

二、交换排序

1、冒泡排序

基本思想：
两两元素相比，前一个比后一个大就交换，直到将最大的元素交换到末尾位置。这是第一趟
一共进行n-1趟这样的交换将可以把所有的元素排好。第i趟需要比较（n-i）次
(n-1趟是因为只剩两个元素时只需要一趟就可以完成)
时间复杂度：
最佳情况：T(n) = O(n)
最差情况：T(n) = O(n^2)
平均情况：T(n) = O(n^2)

//冒泡排序
void  bubble(vector<int>& nums)
{
	int flag = 0;
	for (int i = 0; i < nums.size() - 1; i ++ )//总共有n-1趟，每一趟都确定了最大值，即序列的最后一个元素
	{
		for (int j = 0; j < nums.size()-i-1; j++)//比较n-i次,从0开始，内循环n-i-1次
		{
			if (nums[j] > nums[j + 1])    swap(nums[j], nums[j + 1]);
			flag = 1;
		}
		 //若某一趟排序中没有元素交换则说明所有元素已经有序，不需要再排序
		if (flag == 0)   break;
	}
}

2、快速排序

任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

//快速排序
int   part(vector<int> &nums,int left,int right)
{
	int key = nums[left];
	int hole = left;
	while (left < right)
	{
		//选左边为基准，就从右边开始判断
		while(left<right && nums[right]>= key)
		{
			right--;
		}
		nums[hole] = nums[right];
		hole = right;
		//这时右边多了一个空，就从左边挑选大于key地值
	while (left < right && nums[left] <= key)
		{
			left++;
		}
		nums[hole] = nums[left];
		hole = left;
	}
	//最后left与right相同，就把key值放在中间
	nums[hole] = key;
	return hole;
}
void quick_sort(vector<int> &nums, int left, int right)
{
	if (left >= right)  return;
	int a = part(nums, left, right);
	quick_sort(nums, left, a - 1);
	quick_sort(nums, a + 1, right);
}

时间复杂度：O(N*logN)
空间复杂度：O(logN)
稳定性：不稳定

三、选择排序

1、简单选择排序

时间复杂度：O(N^2)
空间复杂度：O(1)
稳定性：不稳定

//选择排序
void select(vector<int>& nums)
{
	for (int i = 0; i < nums.size() - 1; i++)//总共比较n-1趟
	{
		int key = i;
		for (int j = i + 1; j < nums.size(); j++)//每一个位置都与nums[i]相比较，找出最小值，替换nums[i]
		{
			if (nums[key] > nums[j])   key = j;
		}
		swap(nums[key], nums[i]);
	}
}

2、堆排序

堆的本质就是满足下面性质·的完全二叉树：它的任一非叶子节点均小于或者大于它的孩子节点。
小根堆的根节点值最小，大根堆的根节点值最大。
堆排序指的是：若在输出堆顶的最小值或者最大值之后，使得剩下的n-1个元素的序列又重新建成一个堆，则得到n个元素的次小值或者次大值，如此反复，便能得到一个有序序列，这个过程称为堆排序。
堆排序的两个问题：
1、如何由一个无序序列建成一个堆？
2、如何在输出堆顶元素后，调整剩余元素为一个新的堆？

堆排序：
时间复杂度o(nlogn)
空间复杂度o(1)
不稳定

四、归并排序

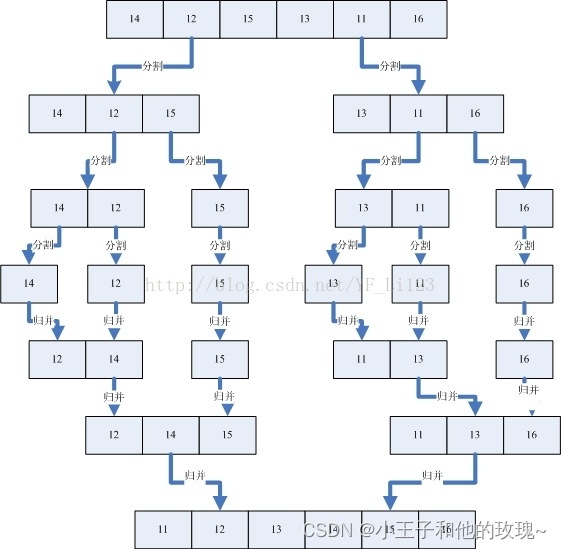
归并排序的基本思想：
将两个或两个以上的有序子序列归并为一个有序子序列

#include<iostream>
#include<vector>
using namespace std;
vector<int> temp;
void merge(vector<int> &nums, int l,int m, int r)
{
	//辅助数组清空，很重要
	temp.clear();
	int i = l; int j = m + 1;
	//双指针法取最小放入辅助数组中
	while (i <= m && j <= r)
	{
		if (nums[i] < nums[j])
		{
			temp.push_back(nums[i]);
			i++;
		}
		else
		{
			temp.push_back(nums[j]);
			j++;
		}
	}
	//如果第一组有剩余放进辅助数组
	while (i <= m)
	{
		temp.push_back(nums[i]);
		i++;
	}
	//如果第二组有剩余，放进辅助数组
	while(j<=r)
	{
		temp.push_back(nums[j]);
		j++;
	}
	//将辅助数组里的值放进数组的对应位置
	for (int k = 0; k < temp.size(); k++)
	{
		nums[l] = temp[k];
		l++;
	}

}
void merge_sort(vector<int>& nums,int l,int r)
{
	if (l < r)
	{
		int m= l + (r - l) / 2;
		merge_sort(nums, l, m);//递归分成两组
		merge_sort(nums, m+1, r);
		merge(nums, l, m,r);//将两组合并
	}
}
void print(vector<int>  nums)
{
	for (int i = 0; i < nums.size(); i++)
	{
		cout << nums[i] << "  ";
	}
}
int main()
{
	vector<int> nums;
	int a;
	while (cin >> a)
	{
		nums.push_back(a);
		if (cin.get() == '\n')  break;
	}
	merge_sort(nums,0,nums.size()-1);
	print(nums);
	return 0;
}

五、各排序算法的时间复杂度比较