二分与前缀和

二分

时间复杂度O(log n).
数据区间：

L----------------mid-----------------R

代码实现：

while(L<R)
{
mid=(L+R+1)/2;
if(mid在L->mid)	L=mid;
else	R=M-1;

}

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式
第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式
共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

3 4
5 5
-1 -1

#include<bits/stdc++.h>
using namespace std;

const int N=100010;

int n,m;
int q[N];

int main()
{
	scanf("%d%d",&n,&m);//n表示数组长度,m表示询问个数 
	for(int i=0;i<n;i++)	scanf("%d",&q[i]);
	

	
	for(int i=0;i<m;i++)
	{
		int x;
		scanf("%d",&x);//输入查询数字
		int l=0,r=n-1;//确定区间 
			
		while(l<r)
		{
			int mid=l+r>>1;
			if(q[mid]>=x)	r=mid;
			else
			l=mid+1;
		}
		if(q[r]==x)
		{
			cout<<r<<' ';
		
			r=n-1;
			while(l<r)
			{
				int mid=l+r+1>>1;
				if(q[mid]<=x)	l=mid;
				else	r=mid-1;
			}
			cout<<r<<endl;
		
		
		}
		else
			cout<<"-1 -1"<<endl; 
}
	return 0;
}

前缀和

一维前缀和：

例：输入一个长度为 n 的整数序列。

接下来再输入 m 个询问，每个询问输入一对 l,r。

对于每个询问，输出原序列中从第 l 个数到第 r 个数的和。

输入格式
第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数数列。

接下来 m 行，每行包含两个整数 l 和 r，表示一个询问的区间范围。

输出格式
共 m 行，每行输出一个询问的结果。

数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000
输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

#include<bits/stdc++.h>
using namespace std;
const int N=1e+5;
int n,m;
int q;
int sum[N];
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)	
	{
		scanf("%d",&q);
		sum[i]=q+sum[i-1];//构建前缀和数组。
	}
	for(int i=1;i<=m;i++)
	{
		int l,r;
		scanf("%d%d",&l,&r);
		int res;
		res=sum[r]-sum[l-1];
		cout<<res<<endl;
	}
	return 0;
}

二维前缀和：

容斥原理

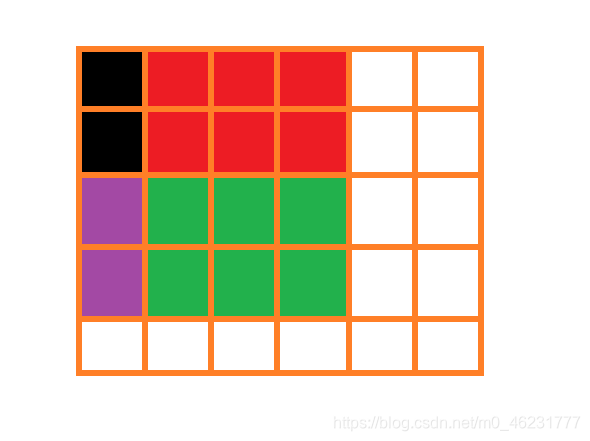
绿色的子矩阵的和=（紫色+黑色）-（红色+黑色）

子矩阵求和：

输入一个 n 行 m 列的整数矩阵，再输入 q 个询问，每个询问包含四个整数 x1,y1,x2,y2，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式
第一行包含三个整数 n，m，q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含四个整数 x1,y1,x2,y2，表示一组询问。

输出格式
共 q 行，每行输出一个询问的结果。

数据范围

1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

#include<bits/stdc++.h>
using namespace std;
const int N=1e5;

int n,m,q;
int temp[N][N];
int sum[N][N];
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&temp[i][j]);
		}
		
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+temp[i][j];
		}
	
	for(int i=1;i<=q;i++)
	{
		int x1,x2,y1,y2;
		scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
		
		int res;
		res=sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1];
		cout<<res<<endl;
	}
	return 0;
}