Search Based Path Planning

Search Based Pathing Planning

参考：https://www.bilibili.com/video/BV1yT4y1T7Eb

Dijkstra

流程

• 从起点开始扩展，每一步为一个节点找到最短路径
• cost：f(n) = g(n)
• g(n)：当前路径，从起点到n的代价（距离）
• While true：
  1. 从open list选择代价最小的节点，收录进closed list
  2. 收录后遍历该节点的所有可访问邻节点，更新cost
• 最优性证明：反证法

特性

完备

最优

算法

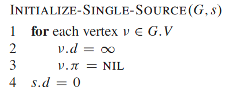
开始

​ 将起点放入 open list

​ While 1

​ if open list 为空

​ 无可行路径，搜索失败

​ 取出 open list 中 cost=g(n) 最小的节点为 current

​ 将 current 放入 closed list

​ if current 为终点

​ 找到路径，结束

​ 遍历 current 的邻节点 neighbour

​ if neighbour为障碍物，跳过

​ if neighbour 已被 closed list 收录，跳过

​ if neighbour 在 open list 中

​ 更新 neighbour g(n)

​ else

​ 计算 neighbour g(n)，加入 open list

结束

效果

A*

motivation

减少收录的栅格数目，增加搜索速度

在Dijkstra上的改进

• cost：f(n) = g(n) + h(n)

• g(n)：当前路径，从起点到n的代价（距离）

• h(n)：启发式函数，一般取当前点到终点的距离

• While true：

  1. 从open list选择代价最小的节点，收录进closed list
  2. 收录后遍历该节点的所有可访问邻节点，更新cost

• 最优性保证：h(n) $\le$ *h(n)

特性

完备

最优

算法

开始

​ 将起点放入 open list

​ While 1

​ if open list 为空

​ 无可行路径，搜索失败

​ 取出 open list 中 cost=g(n)+h(n) 最小的节点为 current

​ 将 current 放入 closed list

​ if current 为终点

​ 找到路径，结束

​ 遍历 current 的邻节点 neighbour

​ if neighbour为障碍物，跳过

​ if neighbour 已被 closed list 收录，跳过

​ if neighbour 在 open list 中

​ 更新 neighbour g(n)

​ else

​ 计算 neighbour g(n)，加入 open list

结束

效果

Jump Point Search

​ 有众多的算法能够在代价一致的均匀网格中（uniform-cost grid maps）搜索最短线性路径，常见的有A*，Dijkstra’s等。而JPS算法相比其他算法，省略了众多点插入和点删除的操作，有选择性地扩展必要的节点。因此有着很高的搜索效率。

原论文：Online Graph Pruning for Pathfinding on Grid Maps by Daniel Harabor and Alban Grastien

符号和术语

• JPS算法工作于不定向的均匀网格地图中。
• 每一次直线运动的代价为1，对角运动的代价为 $\sqrt{2}$。
• 涉及不可穿越节点（障碍物）的运动是禁止的。
• $y=x+k\vec{d}$ 代表从 $x$ 沿 $\vec{d}$ 方向运动 $k$ 个单位可到达 $y$，当 $\vec{d}$ 为对角方向时，可分解为