索引会带来什么弊端？为什么选择B+树作为索引的数据结构？索引都是B+树的？

本文链接：https://blog.youkuaiyun.com/m0_45364328/article/details/125658335

索引会带来什么弊端？

索引是个好东西，由于索引底层是基于B+树的，而查找也在B+树的基础上，利用二分查找的思想加快查找速度。我们今天不讨论索引为什么快，有什么好处，仅仅讨论它有什么坏处，或者有什么代价

索引是个好东西，可不能乱建，它在空间和时间上都会有消耗：

空间上的代价：

每建立一个索引都要为它建立一棵B+树，每一棵B+树的每一个节点都是一个数据页，一个页默认会
占用 16KB 的存储空间，一棵很大的B+树由许多数据页组成，那就是很大的一片存储空间。
时间上的代价：

每次对表中的数据进行增、删、改操作时，都需要去修改各个B+树索引。而且我们讲过，B+树每层节点都是按照索引列的值从小到大的顺序排序而组成了双向链表。不论是叶子节点中的记录，还是内节点中的记录（也就是不论是用户记录还是目录项记录）都是按照索引列的值从小到大的顺序而形成了一个单向链表。而增、删、改操作可能会对节点和记录的排序造成破坏，所以存储引擎需要额外的时间进行一些记录移位，页面分裂、页面回收等操作来维护好节点和记录的排序。如果我们建了许多索引，每个索引对应的B+树都要进行相关的维护操作，会给性能拖后腿。

所以说，索引不是想建就建的，太多的索引，反而弊端会大于优点

为什么选择B+树作为索引的数据结构？索引都是B+树的？

Hash索引

首先我们看下Hash结构：

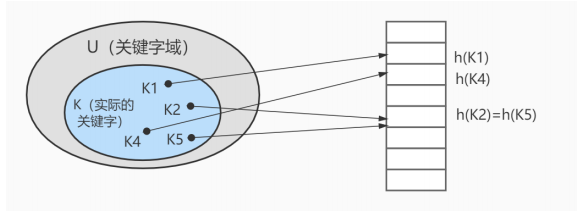
在这里插入图片描述
上图中哈希函数h有可能将两个不同的关键字映射到相同的位置，这叫做碰撞，在数据库中一般采用链接法来解决。在链接法中，将散列到同一槽位的元素放在一个链表中，如下图所示：

Hash结构效率高，那为什么索引结构要设计成树型呢？
由Hash的结构我们也能看出来，Hash中存储的数据不一定连续的，如果仅仅是查找一条数据，通过Hash结构是没有问题的，但是如果是多条呢？也就是SQL中的范围查找，显然用Hash就不合适了，而且Hash还有扩容的问题呢

难道没有使用Hash索引的？还真有。
在这里插入图片描述
Hash索引的适用性：

采用自适应 Hash 索引目的是方便根据 SQL 的查询条件加速定位到叶子节点，特别是当 B+ 树比较深的时候，通过自适应 Hash 索引可以明显提高数据的检索效率。

我们可以通过 innodb_adaptive_hash_index 变量来查看是否开启了自适应 Hash，比如：
在这里插入图片描述

二叉树索引

如果我们利用二叉树作为索引结构，那么磁盘的IO次数和索引树的高度是相关的。

二叉搜索树的特点

创造出来的二分搜索树如下图所示：

为了提高查询效率，就需要减少磁盘IO数。为了减少磁盘IO的次数，就需要尽量降低树的高度，需要把原来“瘦高”的树结构变的“矮胖”，树的每层的分叉越多越好。

AVL树

在这里插入图片描述
针对同样的数据，如果我们把二叉树改成 M 叉树（M>2）呢？当 M=3 时，同样的 31 个节点可以由下面的三叉树来进行存储：

B-Tree

B 树的结构如下图所示：

一个 M 阶的 B 树（M>2）有以下的特性：
1、根节点的儿子数的范围是 [2,M]。
2、每个中间节点包含 k-1 个关键字和 k 个孩子，孩子的数量 = 关键字的数量 +1，k 的取值范围为[ceil(M/2), M]。
3、叶子节点包括 k-1 个关键字（叶子节点没有孩子），k 的取值范围为 [ceil(M/2), M]。
4、假设中间节点节点的关键字为：Key[1], Key[2], …, Key[k-1]，且关键字按照升序排序，即 Key[i] <Key[i+1]。此时 k-1 个关键字相当于划分了 k 个范围，也就是对应着 k 个指针，即为：P[1], P[2], …,P[k]，其中 P[1] 指向关键字小于 Key[1] 的子树，P[i] 指向关键字属于 (Key[i-1], Key[i]) 的子树，P[k]指向关键字大于 Key[k-1] 的子树。
5、所有叶子节点位于同一层

上面那张图所表示的 B 树就是一棵 3 阶的 B 树。我们可以看下磁盘块 2，里面的关键字为（8，12），它有 3 个孩子 (3，5)，(9，10) 和 (13，15)，你能看到 (3，5) 小于 8，(9，10) 在 8 和 12 之间，而 (13，15)大于 12，刚好符合刚才我们给出的特征。

然后我们来看下如何用 B 树进行查找。假设我们想要查找的关键字是 9 ，那么步骤可以分为以下几步：
1、我们与根节点的关键字 (17，35）进行比较，9 小于 17 那么得到指针 P1；
2、按照指针 P1 找到磁盘块 2，关键字为（8，12），因为 9 在 8 和 12 之间，所以我们得到指针 P2；

3、按照指针 P2 找到磁盘块 6，关键字为（9，10），然后我们找到了关键字 9

你能看出来在 B 树的搜索过程中，我们比较的次数并不少，但如果把数据读取出来然后在内存中进行比较，这个时间就是可以忽略不计的。而读取磁盘块本身需要进行 I/O 操作，消耗的时间比在内存中进行比较所需要的时间要多，是数据查找用时的重要因素。 B 树相比于平衡二叉树来说磁盘 I/O 操作要少，在数据查询中比平衡二叉树效率要高。所以只要树的高度足够低，IO次数足够少，就可以提高查询性能。
在这里插入图片描述

B+Tree

B+ 树和 B 树的差异：
有 k 个孩子的节点就有 k 个关键字。也就是孩子数量 = 关键字数，而 B 树中，孩子数量 = 关键字数+1
非叶子节点的关键字也会同时存在在子节点中，并且是在子节点中所有关键字的最大（或最
小）。
非叶子节点仅用于索引，不保存数据记录，跟记录有关的信息都放在叶子节点中。而 B 树中，非叶子节点既保存索引，也保存数据记录。
非叶子节点仅用于索引，不保存数据记录，跟记录有关的信息都放在叶子节点中。而 B 树中，非叶子节点既保存索引，也保存数据记录。

B 树和 B+ 树都可以作为索引的数据结构，在 MySQL 中采用的是 B+ 树。
但B树和B+树各有自己的应用场景，不能说B+树完全比B树好，反之亦然。

思考题：为了减少IO，索引树会一次性加载吗？(按页加载，可能存在预读)
思考题：B+树的存储能力如何？为何说一般查找行记录，最多只需1~3次磁盘IO

假设所有存放用户记录
的叶子节点代表的数据页可以存放 100条用户记录 ，所有存放目录项记录的内节点代表的数据页可以存
放 1000条目录项记录 ，那么：
如果B+树只有1层，也就是只有1个用于存放用户记录的节点，最多能存放 100 条记录。
如果B+树有2层，最多能存放 1000×100=10,0000 条记录。
如果B+树有3层，最多能存放 1000×1000×100=1,0000,0000 条记录。
如果B+树有4层，最多能存放 1000×1000×1000×100=1000,0000,0000 条记录。相当多的记
录！！！