矩阵分析与应用+张贤达

第一章 矩阵与线性方程组（二十一）

1. 广义逆矩阵的计算

令$A_{m\times n}$具有秩$r$。若$A=FG$，其中，$F_{m\times r}$的为$r$(满列秩矩阵)，且$G_{r\times n}$的秩也为$r$(满行秩矩阵)，则称$A=FG$为矩阵$A$的满秩分解

那么，是不是任意一个矩阵都存在满秩分解呢?下面的命题给出了这个问题的肯定答案。
命题1
一个秩为$r$的$m\times n$矩阵$A$可以分解为
$$A=K_{m\times r}Lr\times n$$
式中，K和L分别具有满列秩和满行秩。

算法1(矩阵的满秩分解算法)
(1) 利用行初等变换将矩阵$A$化为阶梯型，即

(2) 对单位矩阵执行逆行初等变换，得到逆矩阵

(3) 利用逆矩阵$P^{-1}$的前$r$列构造矩阵$F$。
(4) 书写满秩分解结果$A=FG$。

(2)中的逆行初等变换如下:

• 第$i$行和第$j$行的互换$R_i\leftrightarrow R_j$，的逆变换是$R_j\leftrightarrow R_i$.
• 初等行变换$a{R}_i$的逆变换为$a^{-1}R$。
• 初等行变换$R_i+a{R}_j$的逆变换为$R_i-a{R}_j$.

一旦获得矩阵$A_{m\times n}$的满秩分解后，即可根据下面的引理求出$A$的广义逆矩阵$A^{-1}$

引理1
若矩阵$A_{m\times n}$，具有秩$r$，且其满秩分解为$A=FG$，其中，$F_{m\times r}$为满列秩;$G_{r\times n}$为满行秩，则
$$A^{-}=G^T(F^{T}A{G}^T{)}^{-1}{F}^T$$
是$A$的一个广义逆矩阵。

算法2(广义逆矩阵的计算)
(1) 计算矩阵$A_{m\times n}$的满秩分解$A=FG$。
(2) 求广义逆矩阵$A^{-}=G^T(F^{T}A{G}^T{)}^{-1}{F}^T$

下面是广义逆矩阵的递推计算公式。
(1) 令$A$是一个$m\times n$矩阵，$u$和$v$分别是$m\times 1$和$n\times 1$向量，则
$$(A+u{v}^T{)}^{-}=A^{-}\frac{(A^{-}u)(v^T{A}^{-})}{1+v^T{A}^{-}u}$$
其中，假定$v^T{A}^{-}u\ne -1$。
(2)分块矩阵的广义逆矩阵的计算公式
若
$$M=\left[\begin{array}{cc}A& C\\ C^H& B\end{array}\right]$$
式中，$A=X_1^H{X}_1,B=X_2^H{X}_2,C=X_1^H{X}_2$。
若$D=B-C^H{A}^{-}C$，则
$$M^{-}=\left[\begin{array}{cc}{A}^{-}+A^{-}C{D}^{-}{C}^H{A}^{-}& -A^{-}C{D}^{-}\\ -D^{-}{C}^H{A}^{-}& D^{-}\end{array}\right]$$

2. 一致方程的最小范数解

举一个简单的例子，假定线性方程为
$$x_1+2x_2=10$$
这显然是一个一致方程。

如下图所示，直线$x_1+2x_2=10$上的所有点$(x_1,x_2)$都是方程的解即通解。
如果希望确定唯一的解，就必须增加某个约束条件，求满足该条件的唯一解。作为约束条件，这里要求得到的解的范数为最小。这样得出的唯一解称为最小范数解。
由于$x$的范数最小等同非向量$x$的端点与原点的距离最小，故最小范数解也称最短距离解。
在本例中，“与原点的距离最短的解”为(2,4)，见下图。

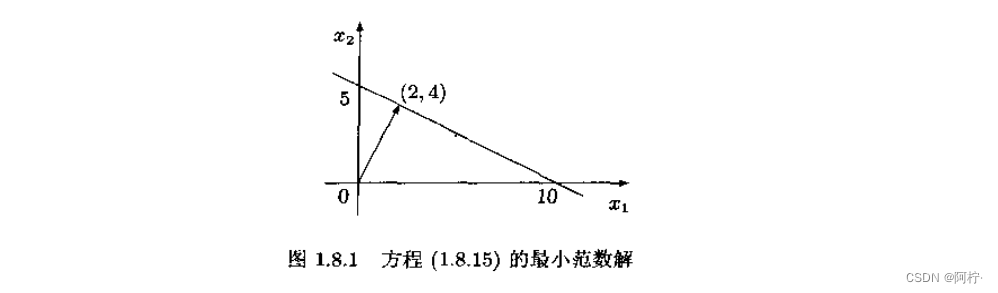
下面讨论一般情况下线性方程$Ax=y$的最小范数解。先讨论其通解。
定理1
令$n\times m$矩阵$A^{-}$是$m\times n$矩阵$A$的任意一个广义逆矩阵，则
(1) 齐次方程$Ax=0$的一个通解为$x=(I-A^{-}A)z$，其中，$z$是$n\times 1$任意向量。

(2) 非齐次方程$Ax=y$为一致方程的充分必要条件是
$$A{A}^{-}y=y$$
(3) 非齐次方程$Ax=y$的一个通解为
$$x=A^{-}y+(I-A^{-}A)z$$
式中，$z$为$n\times 1$任意向量。

由于对一个一致方程$Ax=y$，存在着通解公式，一个令我们感兴趣的问题是:是否存在一个$y$无关的广义逆矩阵$G$选择，使得解$Gy$在所有的解中具有最小范数?换言之，如果广义逆矩阵$G$存在的话，我们希望它满足条件
$$\underset{Ax=y}{\min }||x||=||Gy||$$
如果上式满足，则称$Gy$为线性一致方程$Ax=y$的最小范数解，并称广义逆矩阵$G$为最小范数广义逆矩阵。

考虑矩阵$A_{m\times n}$和向量$x_{n\times 1}{y}_{m\times 1}$。于是，$<Ax,y>$是$m$阶向量空间的内积，记作$<Ax,y{>}_m$。矩阵$A_{m\times n}$的伴随矩阵用符号$A^{\#}$表示，定义为将$m$阶向量空间的内积等价变换为$n$阶向量的内积的一个映射，即有
$$<Ax,y{>}_m=<x,A^{\#}y{>}_n$$
特别地，若$A^{\#}=A$，则称$A$为自伴随矩阵。显然，自伴随矩阵一定是正方矩阵。

伴随矩阵具有以下性质:

(1)$(A^{\#}{)}^{\#}=A$。
(2)$(AB{)}^{\#}=B^{\#}{A}^{\#}$。
(3)$<Ax,By>=0,\forall x,y\leftrightarrow A^{\#}B=O$。
(4)$A^{\#}=A^T$(若$A$为实矩阵)或$A^{\#}=A$(若$A$为复矩阵)。

定理2
$Gy$是一致方程$Ax=y$的最小范数解，当且仅当
$$AGA=A,(GA{)}^{\#}=GA$$

关于最小范数解，有以下两点注释:
注释1 充分必要条件$AGA=A,(GA{)}^{\#}=GA$可以等价写作$GA{A}^{\#}=-A^{\#}$。

注释2 最小范数解是唯一的，虽然最小范数广义逆矩阵$G$有可能不唯一。

特别地，我们来讨论当$A_{m\times n}$具有满行秩$m$时，线性方程$Ax=y$的最小范数解。由于$A$满行秩，故增广矩阵$[A,y]$的秩与$A$的秩相同，即线性方程$Ax=y$是一致方程。另一方面，矩阵乘积$A{A}^H$ 可逆，故存在右伪逆矩阵$A^H(A{A}^H{)}^{-1}$。与之对应的解为
$$x^{°}=A^H(A{A}^H{)}^{-1}y$$

3. 非一致方程的最小二乘解

考虑非一致方程$Ax=y$的求解。由于是非一致方程，故不存在严格满足方程的解。
换言之，非一致方程只能够有近似解。因此，我们很自然地希望寻找一个使得方程两边的误差平方和为最小的解。这样一种解称为非一致方程的最小二乘解。具体说来，若用$\hat{x}$代表最小二乘解，则它应该满足
$$||A\hat{x}-y||=\underset{x}{\inf }||Ax-y||$$
式中，$inf$表示函数的下确界。
定理1
令$G$是某个矩阵，则$\hat{x}=Gy$是非一致方程$Ax=y$的最小二乘解当且仅当
$$A^{\#}AG=A^{\#}$$
或者等价为
$$AGA=A,(AG{)}^{\#}=AG$$
关于非一致方程的最小二乘解，有下面的两点注释:
注释1 非一致方程的最小二乘解有可能不是唯一的，但是不同的最小二乘解得到的$Ax$和$Ax-y$是唯一的。
注释2 非一致方程$Ax=y$的最小二乘解的通解形式火
$$\hat{x}=Gy+(I-GA)z，z任意$$

考虑非一致方程$Ax=y$的矩阵$A$具有满列秩的特殊情况。此时，矩阵乘积$A^{H}A$非奇异。
下面证明，解
$$x°=(A^{H}A{)}^{-1}{A}^{H}y$$
就是一个最小二乘解。

令$x$是任何其他一个解，易知
$$||Ax-y|{|}^2=||A(x-x°)+Ax°-y|{|}^2$$
$$=||A(x-x°)+[A(A^{H}A{)}^{-1}{A}^H-I_m]y|{|}^2$$
$$=||A(x-x°)|{|}^2+||[A(A^{H}A{)}^{-1}{A}^H-I_m]y|{|}^2+2[A(x-x°){]}^H[A(A^{H}A{)}^{-1}{A}^H-I_m]y$$
但是最后一个等式的第三项等于零，即
$$[A(x-x°){]}^H[A(A^{H}A{)}^{-1}{A}^H-I_m]y$$
$$=(x-x°{)}^H[A^{H}A(A^{H}A{)}^{-1}{A}^H-A^H]y$$
$$=(x-x°{)}^H(A^H-A^H)y=0$$
因此，上简化为
$$||Ax-y|{|}^2=||A(x-x°)|{|}^2+||A(A^{H}A{)}^{-1}{A}^{H}y-y|{|}^2$$
$$=||A(x-x°)|{|}^2+||Ax°-y|{|}^2$$
由于$||A(x-x°)|{|}^2>0$，故:
$$||Ax-y|{|}^2\ge ||Ax°-y|{|}^2,\forall x,y$$
即是说，$x°$确实是矩阵$A$满列秩时，非一致方程$Ax=y$的一个最小二乘解。