哈希表
5.1有效的字母异位词
目前没感觉到和hash有什么关系,还感觉有点儿暴力求解的意思。
class Solution {
public:
bool isAnagram(string s, string t) {
int record[26] = {0};
for(int i=0;i<s.size();i++){
record[s[i]-'a'] ++;
}
for(int i=0;i<t.size();i++){
record[t[i]-'a'] --;
}
for(int i=0;i<26;i++){
if(record[i] != 0){
return false;
}
}
return true;
}
};
5.2 两个数组的交集
思路:
- 用unordered_set来存储数组元素
- for(int num:nums2) num代表nums中的每一个元素
若在nums_set找到和nums2中一样的元素,就插入到 result_set 中去 - 返回找到的值
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; //可以给结果集去重
unordered_set<int> num1_set(nums1.begin(),nums1.end());//给nums1去重
for(int num:nums2){
if(num1_set.find(num) != num1_set.end()){//若num1_set find(num)为空则等于end()
result_set.insert(num);
}
}
return vector<int>(result_set.begin(),result_set.end());
}
};
代码随想录更新测试数据范围后,就可以使用数组来做了。随想录数组大小为1005,这里设置1000也可以过。
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; //可以给结果集去重
int hash[1000] = {0};
for(int num:nums1){
hash[num] = 1;
}
for(int num:nums2){
if(hash[num] == 1){
result_set.insert(num);
}
}
return vector<int>(result_set.begin(),result_set.end());
}
};
5.3 快乐数
一个数的各个位求平方加起来得到新数,判断是否为1,不为1,则再将新数的各个位求平方再加和,如此循环,要么为1,要么无限循环。
将每次的计算结果插入 unordered_set 中,相同的数只记录一次,unordered_set中重复的数只记录一次。下次循环得到新的数后,在unordered_set中寻找,如果找到了,说明求和结果无限循环,该数不是快乐数,跳出循环程序。
class Solution {
public:
int getSum(int n){
int sum = 0;
while(n){
sum += (n%10) * (n%10);
n = n/10;
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> rst;
while(1){
int sum = getSum(n);
if(sum == 1){
return true;
}
if(rst.find(sum) != rst.end()){
return false;
}
else{
rst.insert(sum);
}
n = sum;
}
}
};
5.4 两数之和
当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
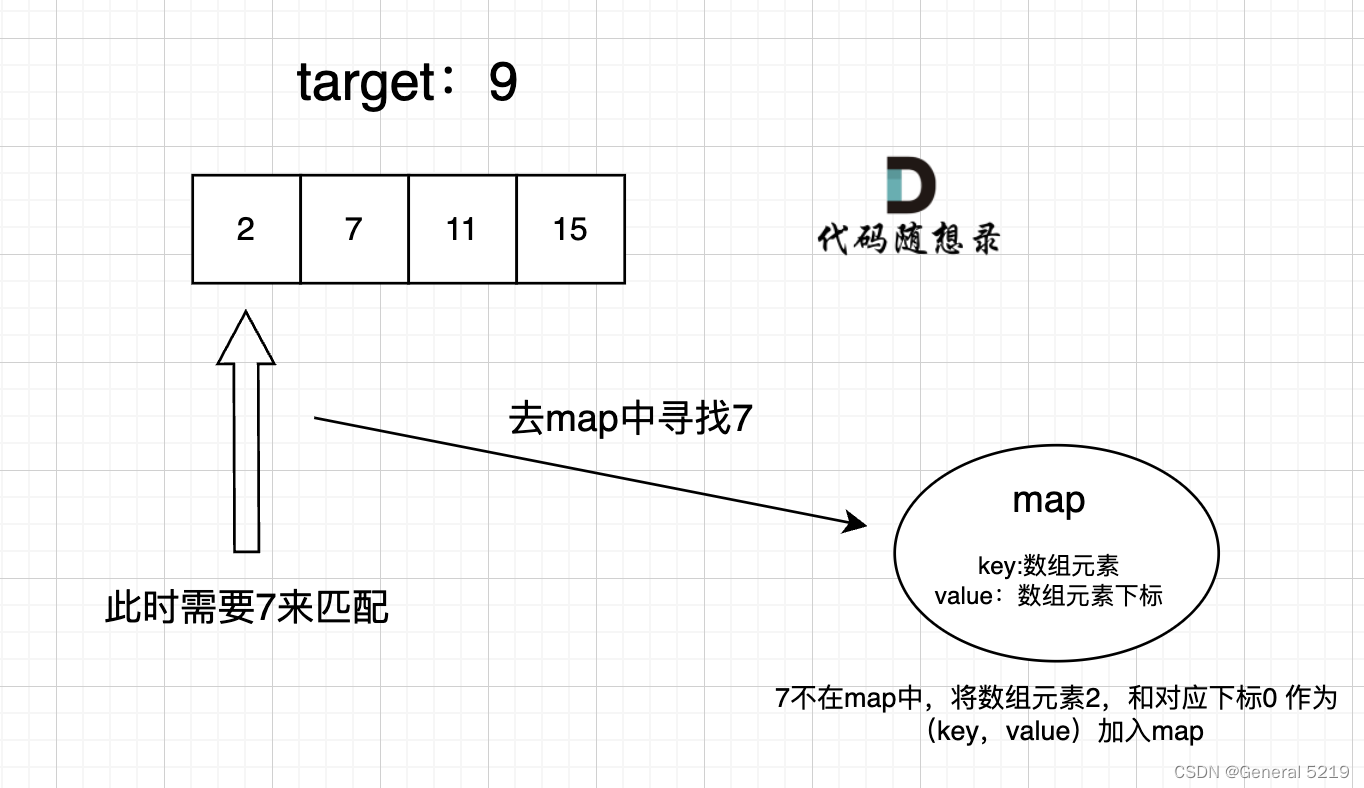

采用 “键值对” 或者 “insert” 方法插入都可以
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
std::unordered_map<int,int> map;
for(int i=0;i<nums.size();i++){
auto iter = map.find(target-nums[i]);
if(iter != map.end()){
return {iter->second,i};
}
else{
//map.insert(pair<int,int>(nums[i],i));
map[nums[i]] = i;//键值对方式插入
}
}
return {};
}
};
思考:1. 为什么想到会用哈希
当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
2. 哈希表为什么用map
为了同时能保留数据元素的下标
3. 本题的map用来存放什么
用来存放遍历过的数组元素的值和下标
4. map中的key和value用来存放什么
key用来存放数组元素值,value用来存放下标
5.5 四数相加
首先定义一个unordered_map,用来存放a+b的结果,这里用a+b的值为key,value为a+b值出现的次数。这样就记录了所有的a+b的值,并且用该值作索引,记录了其出现次数。
然后又是两层for循环,计算出所有 c+d 的结果,因为题目要求相加得0,可以反推一下需要的 a+b 的值,并以此为key,读出符合要求的a+b出现的次数,计入cnt中,循环完成后直接返回即可。
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
unordered_map<int,int> umap;//其中key为a+b,value为a+b出现的次数
for(int a:nums1){
for(int b:nums2){
umap[a+b]++;
}
}
int cnt = 0;//记录a+b+c+d为0出现的次数
for(int c:nums3){
for(int d:nums4){
if(umap.find(0 - (c+d)) != umap.end()){
cnt += umap[0 - (c+d)];
}
}
}
return cnt;
}
};
5.6.1 赎金信_暴力解法
两层循环,外层循环遍历magnize中元素,内层循环遍历ransomNote中元素,对于每一个外层元素,用内层元素一一比较,有相同的就将该内层元素删除掉。循环完成后,判断ransomNote是否为空。
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
for(int i=0;i<magazine.size();i++){
for(int j=0;j<ransomNote.size();j++){
if(ransomNote[j] == magazine[i]){
ransomNote.erase(ransomNote.begin()+j);
}
}
}
if(ransomNote.length() == 0){
return true;
}
return false;
}
};
5.6.2 赎金信_哈希解法
有点类似 有效字母的异位词,题目中明确字符串中涉及到的都是小写字母,所以可以建立一个长度为26字母长度的数组。首先遍历大数组magnize,记录每个字母出现的次数。然后遍历小数组ransomNote,将相应字母位置上的次数减1,如果字母数组出现负数,则大数组不能够覆盖小数组。
这里有一个逻辑不同,小数组有几个重复的字母,大数组也需要有几个重复的字母才能实现覆盖,所以这里是需要记录重复元素的。
class Solution {
public:
bool canConstruct(string ransomNote, string magazine) {
int hashtab[26] = {0};
if(ransomNote.length()>magazine.length()){
return false;
}
// for(int i=0;i<magazine.length();i++){
// hashtab[magazine[i] - 'a'] ++;
// }
for (const auto& c : magazine) {
hashtab[c - 'a']++;
}
for(const auto& b : ransomNote){
hashtab[b-'a']--;
if(hashtab[b-'a']<0)
return false;
}
// for(int j=0;j<ransomNote.length();j++){
// hashtab[ransomNote[j]-'a']--;
// if(hashtab[ransomNote[j]-'a']<0)
// return false;
// }
return true;
}
};
5.7.1 三数之和_双指针法
双指针法:可以先看 随想录 动画演示,对算法寻找过程有一个了解。
如果定义找到的符合要求的三个数为一个元祖,那么这道题目的要求是,元祖不能重复,但是元组内的数可以重复。
一个元祖内的三个数依次记为a,b,c,则a,b,c可以相同,但是{a,b,c}组成的元祖不可以重复。
所以这道题目关键在于去重:
对于a去重,判断 nums[i] == nums[i-1], 不要用nums[i] == nums[i+1],a后面数组的元素有可能可以给b使用。使用nums[i] == nums[i+1]会跳过符合要求的元素。
对于b和c去重,一定是找到符合要求的一个元祖后再去重。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> result;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++){
if(nums[i]>0){
break;
}
if(i>0 && nums[i] == nums[i-1]){
continue;
}
int left = i+1;
int right = nums.size()-1;
unordered_set<int> set;
while(right>left){
if(nums[i]+nums[left]+nums[right]>0) right--;
else if(nums[i]+nums[left]+nums[right]<0) left++;
else{
result.push_back(vector<int>{nums[i],nums[left],nums[right]});
while(right>left && nums[left]==nums[left+1])left++;
while(right>left && nums[right]==nums[right-1])right--;
left++;
right--;
}
}
}
return result;
}
};
5.7.2 三数之和_哈希
用例会超时,读不懂,先过吧!
5.8 四数之和_双指针
不能只是判断 nums[i] > target时候就直接break,例如 [-4,-3,-2,-1],target = -10,负数情况下越加越小。
所以需要增加判断条件。
if(nums[i]>target &&(nums[i]>=0 || target >= 0))
&&后面的条件有一个就行。
二级剪枝需要前两个节点一起判断。k单独去重就可以了。
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
vector<vector<int>> result;
sort(nums.begin(),nums.end());
for(int i=0;i<nums.size();i++){
//nums[i]剪枝
if(nums[i]>target && nums[i]>=0) break;
//nums[i]去重
if(i>0 && nums[i] == nums[i-1]){
continue;
}
for(int k=i+1;k<nums.size();k++){
//二级剪枝处理
if(nums[i]+nums[k]>target && nums[i]+nums[k]>=0) break;
//nums[k]去重
if(k>i+1 && nums[k] == nums[k-1]){
continue;
}
int left = k+1;
int right = nums.size()-1;
while(right>left){
if(nums[i]+nums[k]+nums[left]+nums[right]>target)right--;
else if(nums[i]+nums[k]+nums[left]+nums[right]<target)left++;
else{
result.push_back(vector<int>{nums[i],nums[k],nums[left],nums[right]});
left++;
right--;
}
}
}
}
return result;
}
};
























 194
194

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








