leetcode-124. 二叉树中的最大路径和

manba_

已于 2025-01-12 11:07:43 修改

阅读量217

点赞数 10

分类专栏： leetcode hot100 文章标签： leetcode 算法

于 2024-10-10 17:36:32 首次发布

本文链接：https://blog.youkuaiyun.com/m0_38098373/article/details/142827614

版权

leetcode hot100 专栏收录该内容

100 篇文章

订阅专栏

题目描述

二叉树中的路径被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

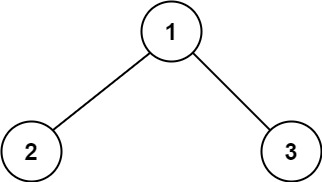
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

思路

官方的思路写的很好. - 力扣（LeetCode）

1）先计算每个节点的最大贡献值【就是在以该节点为根节点的子树中寻找以该节点为起点的一条路径，使得该路径上的节点值之和最大】

2）该节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，如果子节点的最大贡献值为正，则计入该节点的最大路径和，否则不计入该节点的最大路径和。维护一个全局变量 maxSum 存储最大路径和，在递归过程中更新 maxSum 的值，最后得到的 maxSum 的值即为二叉树中的最大路径和。

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.max_sum = float('-inf')

    def max_gain(self, root):
        if not root:
            return 0
        lgain = max(self.max_gain(root.left),0)
        rgain = max(self.max_gain(root.right),0)
        self.max_sum = max(self.max_sum, root.val+lgain+rgain)
        return root.val + max(lgain,rgain)

    def maxPathSum(self, root):
        """
        :type root: TreeNode
        :rtype: int
        """
        self.max_gain(root)
        return self.max_sum

二刷：

后序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):
    def __init__(self):
        self.max_num=float('-inf')
    def max_gain(self, root):
        if not root:
            return 0
        lgain = max(self.max_gain(root.left),0)
        rgain = max(self.max_gain(root.right), 0)
        self.max_num = max(self.max_num, root.val+lgain+rgain)
        # 后序遍历，求路径最大和，左右子节点最大贡献度加自己的
        return root.val + max(lgain,rgain) 
        # 求每个节点的最大贡献度，只能左右分支选其中一个，为了是往上层走。
        # 两个都选，路径走不到的

    def maxPathSum(self, root):
        """
        :type root: Optional[TreeNode]
        :rtype: int
        """
        self.max_gain(root)
        return self.max_num

记忆点：

先求每个节点自身的最大贡献度，后序遍历