Leetcode-74-搜索二维矩阵

题目描述

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：
每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 3
输出：true

示例 2：
输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,50]], target = 13
输出：false

示例 3：
输入：matrix = [], target = 0
输出：false

思路分析

既然这是一个查找元素的问题，并且数组已经排好序，我们自然可以想到用二分查找是一个高效的查找方式。
输入的 m x n 矩阵可以视为长度为 m x n的有序数组：

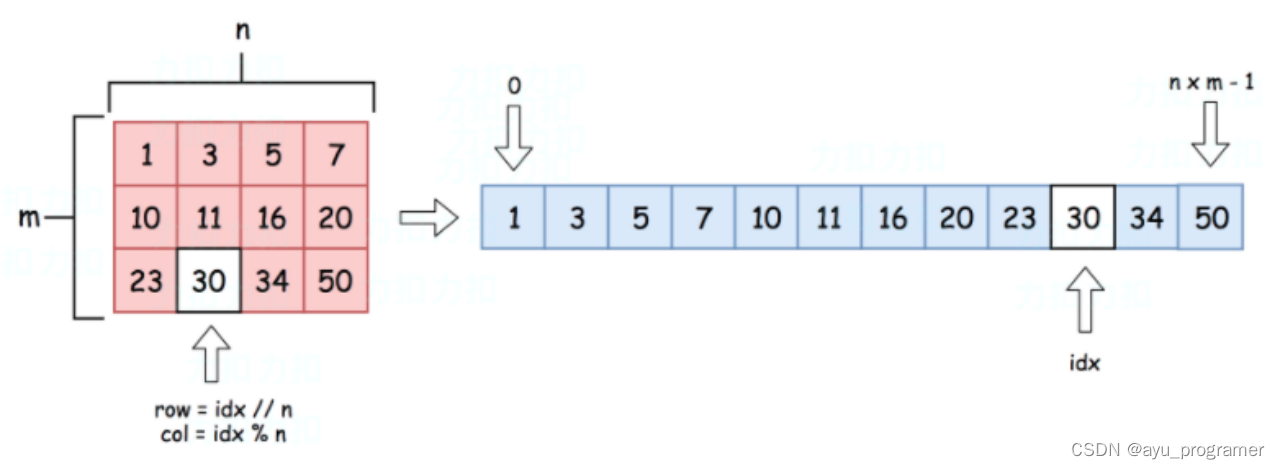
行列坐标为(row, col)的元素，展开之后索引下标为idx = row * n + col；反过来，对于一维下标为idx的元素，对应二维数组中的坐标就应该是：
row = idx / n; col = idx % n;

代码实现

public class SearchMatrix {
    public boolean searchMatrix(int[][] matrix, int target){
        int m = matrix.length;
        if (m == 0) return false; 
        int n = matrix[0].length;
        int left = 0;
        int right = m * n - 1;

// 二分查找，定义左右指针
        while ( left <= right ){
            int midIdx = (left + right) / 2;   
            int midElement = matrix[midIdx/n][midIdx%n];
            if ( midElement < target )
                left = midIdx + 1; 
            else if ( midElement > target )
                right = midIdx - 1; 
            else
                return true;    // 找到target
        }

        return false;
    }
}

复杂度分析
时间复杂度 : 由于是标准的二分查找，时间复杂度为O(log(m n))。
空间复杂度 : 没有用到额外的空间，复杂度为O(1)。