基于yale人脸库的人脸图像检测

一．嵌入式特征选择：

将特征选择方法和学习训练过程融为一体。两者同在一个优化过程中完成。在学习器训练时自动进行特征选择。

给定训练集，考虑线性回归模型，以平方误差为损失函数，则优化目标为：

 

当样本特征较多，样本数量较少时，很容易过拟合。

若采用L1正则化，则有：

 

 二． 人脸图片处理

读入训练图片，将每张人脸图片信息存储为一维矩阵（1*10304），方便计算。

 

 

三．稀疏表示

假设我们用一个M*N的矩阵表示数据集X，每一行代表一个样本，每一列代表样本的一个属性，一般而言，该矩阵是稠密的，即大多数元素不为0。

稀疏表示的含义是，寻找一个系数矩阵A（K*N）以及一个字典矩阵B（M*K），使得B*A尽可能的还原X，且A尽可能的稀疏。A便是X的稀疏表示。

表达为优化问题的话，字典学习的最简单形式为:

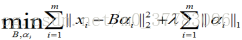求解上述最优化问题的总体策略是，对字典B以及样本稀疏表示alphai交替迭代优化。即先初始化字典B，1.固定字典B对alphai进行优化。2.固定A对字典B进行优化。重复上述两步，求得最终B以及X的稀疏表示A。

 

四．具体迭代求解过程

 参见周志华西瓜书

五 .代码实现

import numpy as np
from PIL import Image
def LoadData(t):
    testp=np.array(Image.open("./feret/"+str(t)+"-6.bmp"))
    testp=np.reshape(testp,(10304,1))
    for i in np.arange(3,8):
     for j in np.arange(1,6):
        if i==3 and j==1:
            img = np.array(Image.open('./feret/' + str(i) + '-' + str(j) + ".bmp"))
            img = np.reshape(img, (112 * 92, 1))
            A = img
        else:
            img = np.array(Image.open('./feret/' + str(i) + '-' + str(j) + ".bmp"))
            img = np.reshape(img, (112 * 92, 1))
            A = np.concatenate((A, img), axis=1)
    A = dfc(A)
    data = testp / np.linalg.norm(testp, ord=2)
    return A, data
def dfc(A):
  m=A.shape[1]
  for i in range(m):
   if i==0:
      Cl=A[:,i]/np.linalg.norm(A[:,i],ord=2)
      Cl=np.reshape(Cl,(10304,1))
   else:
      Cf=A[:,i]/np.linalg.norm(A[:,i],ord=2)
      Cf=np.reshape(Cf,(10304,1))
      Cl=np.concatenate((Cl,Cf),axis=1)
  return Cl

def xishu(A,y):

 x0=np.ones((25,1))
 c=np.dot(A, A.T)
# L=np.linalg.norm(2*np.dot(A,A.T))
 L=100000
 k=0
 while True:
# gradient
  g=2*np.dot(np.dot(A.T,A),x0)-2*np.dot(A.T,y)
  z=x0-1.0/L*g
  lamda=1
  w0=np.linalg.norm(np.dot(A,x0)-y,ord=2)**2+lamda*np.linalg.norm(x0,ord=1)
  x=x0
  for i in range(25):
    if z[i,0]>lamda/L:
      x[i,0]=z[i,0]-lamda/L
    elif z[i,0]<-lamda/L:
      x[i,0]=z[i,0]+lamda/L
    else:
      x[i,0]=0
  k+=1
  w=np.linalg.norm(np.dot(A,x)-y,ord=2)**2+lamda*np.linalg.norm(x,ord=1)
  if w0-w<1e-5:
   return x
  x0=x
def NewX(x,i):

 newX=np.zeros((25,1))

 for t in np.arange(5*i,5*i+5):

   newX[t,0]=x[t,0]

 return newX



def judgeClass(A,x,y):
 minValue=float(np.inf)
 minIndex=-1
 for i in range(5):
   dis=np.linalg.norm(y-np.dot(A,NewX(x,i)))
   print("对类", i + 3, "差异度为： ", dis)
   if dis <= minValue:
    minValue = dis
    minIndex = i
 return minIndex + 3

if __name__=="__main__":
 m=5
 print("Start testing...")
 A,y=LoadData(m)
 cl=xishu(A,y)
 print(m,"最有可能在类",judgeClass(A,cl,y),"中")
 print("end.....")

测试结果：

Start testing...
对类 3 差异度为：  0.896147086781208
对类 4 差异度为：  0.9289496025653518
对类 5 差异度为：  0.8444729557298922
对类 6 差异度为：  0.9006976395753198
对类 7 差异度为：  0.8783348199837376
5 最有可能在类 5 中
end.....