数据结构和算法系统梳理

 

目录

数据结构和算法的重要性

排序算法

冒泡排序

选择排序

插入排序

希尔排序

快速排序

链表：Linked list

  单链表

---

数据结构和算法

算法
1) 算法是程序的灵魂，即使数据繁杂好的算法依然可以让程序保持高速运转！！！
2) 算法是程序使用了的内存计算框架(比如 Spark)和缓存技术(比如 Redis 等)等的核心，可以用来优化程序。

经典语段：
       如果说 Java 是自动档轿车，C 就是手动档吉普。数据结构呢？是变速箱的工作原理。
你可以不知道变速箱怎样工作，就能开车，而且未必就比懂得的人慢。写程序类似，经验可以起到很大作用，但如果你不知道底层是怎么工作的，就永远只能开车，既不会修车，也不能造车。

数据结构和算法的关系

1) 数据结构 (data structure)是一门 研究组织数据方式的学科，可以提高代码效率等。
2) 数据结构是算法的基础, 程序 = 数据结构 +  算法

线性结构和非线性结构
数据结构包括：线性结构和非线性结构。

线性结构
1) 线性结构作为最常用的数据结构，其特点是 数据元素之间是 一对一 的线性关系。
2) 线性结构有两种不同的存储结构，即 顺序存储结构( 数组)和 链式存储结构( 链表)。
3) 线性结构常见的有： 数组、队列、链表和栈。。。

非线性结构
非线性结构包括：二维数组，多维数组，广义表，

 

稀疏数组：

当一个数组中大部分元素为０，或者为同一个值的数组时，可以使用稀疏数组来保存该数组。
1) 记录数组 一共有几行几列，有多少个不同的值
2) 把具有不同值的元素的行列及值记录在一个小规模的数组中，从而 缩小程序的规模

​

队列：
1) 队列是一个 有序列表，可以用 数组或是 链表来实现。
2) 遵循 先入先出的原则。

排序算法

排序算法

排序也称排序算法(SortAlgorithm)，将 一组数据，依 指定的顺序进行 排列的过程。

排序的分类：

内部排序和外部排序，外部排序就是因为数据量过大，无法全部加载到内存中内存和外部存储结合进行排序，内部排序包括如下：

插入排序（直接排序+希尔排序）

选择排序（简单选择+堆排序）

交换排序（冒泡排序+快速排序）

归并排序、

基数排序。

算法的时间复杂度：

度量一个程序(算法)执行时间性能，因为事后统计时间要求和资源浪费就用事前估算法，就要算时间复杂度！so。。。来研究时间复杂度。

时间频度：就是一个算法中语句的执行次数 T(n)

时间复杂度：算法中的基本操作语句的重复执行次数是 n 的某个函数，用 T(n)表示，若有某个辅助函数 f(n)，使得当 n 趋近于无穷大时，T(n) / f(n) 的极限值为不等于零的常数，则称 f(n)是 T(n)的同数量级函数。记作 T(n)= Ｏ( f(n) )，称Ｏ( f(n) ) 为算法的渐进时间复杂度，简称时间复杂度。

3) 计算时间复杂度的方法：

去掉常数项、去掉低阶项、去掉系数！

1) 常数阶 O(1)

2) 对数阶 O(log2n) 单纯while循环

3) 线性阶 O(n) 单纯for循环

4) 线性对数阶 O(nlog2n) for循环里面嵌套while循环

5) 平方阶 O(n^2) 双重for循环

6) 立方阶 O(n^3) 三层for循环

7) k 次方阶 O(n^k) K层for循环

8) 指数阶 O(2^n) 尽量避免 if else？。。。待研究

时间复杂度由小到大：Ο(1)＜Ο(log2n)＜Ο(n)＜Ο(nlog2n)＜Ο(n2)＜Ο(n3)＜ Ο(nk) ＜Ο(2n) ，随着问题规模 n 的不断增大，上述时间复杂度不断增大，算法的执行效率越低对数阶O(log2n), 线性对数阶O(nlog2n)，除了常数阶以外，该种效率最高

空间复杂度：(Space Complexity)为该算法所耗费的存储空间，它也是 问题规模 n 的函数。时间复杂度才是算法分析时看重的。 因为程序执行的速度是用户感官直接的体验。一些缓存产品(redis, memcache)和算法(基数排序)本质就是用空间换时间。

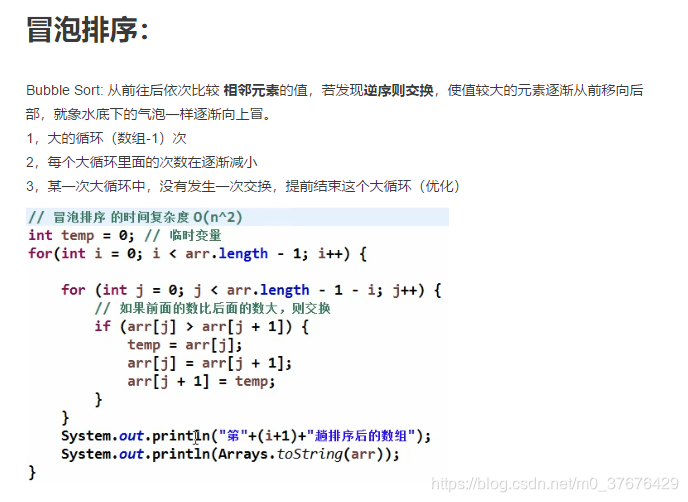
冒泡排序：

Bubble Sort: 从前往后依次比较 相邻元素的值，若发现逆序则交换，使值较大的元素逐渐从前移向后部，就象水底下的气泡一样逐渐向上冒。

1，大的循环（数组-1）次

2，每个大循环里面的次数在逐渐减小

3，某一次大循环中，没有发生一次交换，提前结束这个大循环（优化）

​

​

冒泡排序

​

动图表示：

冒泡排序：代码+优化 优化就是加一个标志位，如果某一次循环有几次没有交换过，所以加入一个标志位。

package com.leo.sort;

import java.util.Arrays;

public class BubbleSort {
	public static void main(String[] args) {
		int arr[] = {3,9,-1,10,-2};
		bubbleSort(arr);
		System.out.println(Arrays.toString(arr));
	}
	public static void bubbleSort(int[] arr) {
		// 冒泡排序 的时间复杂度 O(n^2), 自己写出
		int temp = 0; // 临时变量
		boolean flag = false; // 标识变量，表示是否进行过交换
		for (int i = 0; i < arr.length - 1; i++) {

			for (int j = 0; j < arr.length - 1 - i; j++) {
				// 如果前面的数比后面的数大，则交换
				if (arr[j] > arr[j + 1]) {
					flag = true;
					temp = arr[j];
					arr[j] = arr[j + 1];
					arr[j + 1] = temp;
				}
			}
			if (!flag) { // 在一趟排序中，一次交换都没有发生过
				break;
			} else {
				flag = false; // 重置flag!!!, 进行下次判断
			}
		}
	}
 
}

 

选择排序

学习排序的时候呢 就是把复杂的东西先转化成简单的东西，如果直接写循环？那谁能直接写？主要是思想不对了。

选择排序select sorting：

算法思想：选择排序，从头至尾扫描序列，找出最小的一个元素，和第一个元素交换，接着从剩下的元素中继续这种选择和交换方式，最终得到一个有序序列。

第一次从 arr[0]~arr[n-1]中选取最小值，与 arr[0]交换
第二次从 arr[1]~arr[n-1]中选取最小值，与 arr[1]交换
第三次从 arr[2]~arr[n-1]中选取最小值，与 arr[2]交换，
第 n-1 次从 arr[n-2]~arr[n-1]中选取最小值，与 arr[n-2]交换，共计 n-1 次，得到一个按排序码从小到大排列的有序序列。

package com.leo.sort;

import java.text.SimpleDateFormat;
import java.util.Date;

//选择排序
public class SelectSort {
	public static void main(String[] args) {
		
		//创建100000个数的随机的数组
		int[] arr = new int[100000];
		for (int i = 0; i < 100000; i++) {
			arr[i] = (int) (Math.random() * 1000000); 
		}
		
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("排序前的时间是:" + date1Str);
		selectSort(arr);
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("排序后的时间是:" + date2Str);
        
	}
	
	//选择排序
	public static void selectSort(int[] arr) {
		//选择排序时间复杂度是 O(n^2)
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			int min = arr[i];
			for (int j = i + 1; j < arr.length; j++) {
				if (min > arr[j]) { // 说明假定的最小值，并不是最小
					min = arr[j]; // 重置min
					minIndex = j; // 重置minIndex
				}
			}
			// 将最小值，放在arr[0], 即交换
			if (minIndex != i) {
				arr[minIndex] = arr[i];
				arr[i] = min;
			}
		}
		
	}

}

性能比冒泡好。注意选择排序与冒泡排序的区别：冒泡排序通过依次交换相邻两个顺序不合法的元素位置，从而将当前最小（大）元素放到合适的位置；而选择排序每遍历一次都记住了当前最小（大）元素的位置，最后仅需一次交换操作即可将其放到合适的位置。

        选择排序是给每个位置选择当前元素最小的，比如给第一个位置选择最小的，在剩余元素里面给第二个元素选择第二小的，依次类推，直到第n - 1个元素，第n个元素不用选择了，因为只剩下它一个最大的元素了。那么，在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等 的元素后面，那么交换后稳定性就被破坏了。就是原数组等的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法。

插入排序

        属于内部排序法，是对于要排序的元素以插入的方式找寻该元素的适当位置，以达到排序的目的。
插入排序 Insertion Sorting ：把 n  个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含一个元素，无序表中包含有 n-1  个元素，排序过程中每次从无序表中取出第一个元素，把它的排序码依次与有序表元素的排序码进行比较，将它插入到有序表中的适当位置，使之成为新的有序表。

        插入排序示意图：

动图表示：

上代码：

package com.leo.sort;

import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;

public class InsertSort {
	public static void main(String[] args) {
		//int[] arr = {101, 34, 119, 1, -1, 89}; 
		// 创建要给80000个的随机的数组
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
		}

		System.out.println("插入排序前");
		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("排序前的时间是=" + date1Str);
		insertSort(arr); //调用插入排序算法	
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("排序前的时间是=" + date2Str);	
	}
	
	//插入排序
	public static void insertSort(int[] arr) {
		int insertVal = 0;
		int insertIndex = 0;
		//使用for循环来把代码简化
		for(int i = 1; i < arr.length; i++) {
			//定义待插入的数
			insertVal = arr[i];
			insertIndex = i - 1; // 即arr[1]的前面这个数的下标
	
			// 给insertVal 找到插入的位置
			// 1. insertIndex >= 0 保证在给insertVal 找插入位置，不越界
			// 2. insertVal < arr[insertIndex] 待插入的数，还没有找到插入位置
			// 3. 就需要将 arr[insertIndex] 后移
			while (insertIndex >= 0 && insertVal < arr[insertIndex]) {
				arr[insertIndex + 1] = arr[insertIndex];// arr[insertIndex]
				insertIndex--;
			}
			// 当退出while循环时，说明插入的位置找到, insertIndex + 1
			// 举例：理解不了，我们一会 debug
			//这里我们判断是否需要赋值
			if(insertIndex + 1 != i) {
				arr[insertIndex + 1] = insertVal;
			}

		}
			
	}

}

存在问题： 当 需要插入的数是较小的数时， 后移的次数明显增多，对 效率有影响.

所以优化一下插入排序----就是希尔排序！

希尔排序

       希尔（Donald Shell）提出于1959 年 。简单插入排序Plus版本，也叫缩小增量排序。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含
的关键词越来越多， 当增量减至 1  时，整个文件恰被分成一组，算法终止。

就是在简单插入排序之前加入几个‘’优化步骤‘’。就是在交换时候不要发现一个交换一个！！！

动图：

代码：

package com.leo.sort;

import java.text.SimpleDateFormat;
import java.util.Date;

public class 希尔排序 {

	public static void main(String[] args) {
		
		// 创建要给80000个的随机的数组
		int[] arr = new int[80000];
		for (int i = 0; i < 80000; i++) {
			arr[i] = (int) (Math.random() * 8000000); // 生成一个[0, 8000000) 数
		}

		Date data1 = new Date();
		SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-dd HH:mm:ss");
		String date1Str = simpleDateFormat.format(data1);
		System.out.println("排序前的时间是=" + date1Str);
		
		shellSort(arr);//移位方式
		
		Date data2 = new Date();
		String date2Str = simpleDateFormat.format(data2);
		System.out.println("排序前的时间是=" + date2Str);
	}

	public static void shellSort(int[] arr) {
		
		int temp = 0;
		int count = 0;
		// 根据前面的逐步分析，使用循环处理
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			for (int i = gap; i < arr.length; i++) {
				// 遍历各组中所有的元素(共gap组，每组有个元素), 步长gap
				for (int j = i - gap; j >= 0; j -= gap) {
					// 如果当前元素大于加上步长后的那个元素，说明交换
					if (arr[j] > arr[j + gap]) {
						temp = arr[j];
						arr[j] = arr[j + gap];
						arr[j + gap] = temp;
					}
				}
			}
		}
	}
	
	//对交换式的希尔排序进行优化->移位法
	public static void shellSort2(int[] arr) {
		
		// 增量gap, 并逐步的缩小增量
		for (int gap = arr.length / 2; gap > 0; gap /= 2) {
			// 从第gap个元素，逐个对其所在的组进行直接插入排序
			for (int i = gap; i < arr.length; i++) {
				int j = i;
				int temp = arr[j];
				if (arr[j] < arr[j - gap]) {
					while (j - gap >= 0 && temp < arr[j - gap]) {
						//移动
						arr[j] = arr[j-gap];
						j -= gap;
					}
					//当退出while后，就给temp找到插入的位置
					arr[j] = temp;
				}

			}
		}
	}

}

快速排序

快速排序（Quicksort）是对冒泡排序Plus版本。基本思想是：通过一趟排序将要排序的数据分割成独立的两
部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排
序， 整个排序过程可以递归进行，以此达到整个数据变成有序序列。

快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：

• 从数列中挑出一个元素，称为 “基准”（pivot）；
• 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
• 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

动图演示：

代码：

function quickSort(arr, left, right) {
    var len = arr.length,
        partitionIndex,
        left = typeof left != 'number' ? 0 : left,
        right = typeof right != 'number' ? len - 1 : right;
 
    if (left < right) {
        partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex-1);
        quickSort(arr, partitionIndex+1, right);
    }
    return arr;
}
 
function partition(arr, left ,right) {     // 分区操作
    var pivot = left,                      // 设定基准值（pivot）
        index = pivot + 1;
    for (var i = index; i <= right; i++) {
        if (arr[i] < arr[pivot]) {
            swap(arr, i, index);
            index++;
        }       
    }
    swap(arr, pivot, index - 1);
    return index-1;
}
 
function swap(arr, i, j) {
    var temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

还要再好好的看下！！！
 

链表：Linked list

1) 链表是以节点的方式来存储, 是链式存储。
2) 每个节点包含 data 域，存数据。 next 域：指向下一个节点。
3) 链表的各个节点不一定是连续存储。
4) 链表分 带头节点的链表和 没有头节点的链表，根据实际的需求来确定。

单链表：

• 增加
   
• 修改
   
• 删除

  package com.leo.linkedlist;
  
  import java.util.Stack;
  
  public class SingleLinkedListDemo {
  	public static void main(String[] args) {
  		//进行测试
  		//先创建节点
  		HeroNode hero1 = new HeroNode(1, "宋江", "及时雨");
  		HeroNode hero2 = new HeroNode(2, "卢俊义", "玉麒麟");
  		HeroNode hero3 = new HeroNode(3, "吴用", "智多星");
  		HeroNode hero4 = new HeroNode(4, "林冲", "豹子头");	
  		//创建要给链表
  		SingleLinkedList singleLinkedList = new SingleLinkedList();	
  		//加入
  		singleLinkedList.add(hero1);
  		singleLinkedList.add(hero4);
  		singleLinkedList.add(hero2);
  		singleLinkedList.add(hero3);	
  	}
  }
  
  
  //定义SingleLinkedList 管理我们的英雄
  class SingleLinkedList {
  	//先初始化一个头节点, 头节点不要动, 不存放具体的数据
  	private HeroNode head = new HeroNode(0, "", "");
  	//返回头节点
  	public HeroNode getHead() {
  		return head;
  	}
  
  	//添加节点到单向链表
  	//思路，当不考虑编号顺序时
  	//1. 找到当前链表的最后节点
  	//2. 将最后这个节点的next 指向 新的节点
  	public void add(HeroNode heroNode) {
  		
  		//因为head节点不能动，因此我们需要一个辅助遍历 temp
  		HeroNode temp = head;
  		//遍历链表，找到最后
  		while(true) {
  			//找到链表的最后
  			if(temp.next == null) {//
  				break;
  			}
  			//如果没有找到最后, 将将temp后移
  			temp = temp.next;
  		}
  		//当退出while循环时，temp就指向了链表的最后
  		//将最后这个节点的next 指向 新的节点
  		temp.next = heroNode;
  	}
  	
  	//第二种方式在添加英雄时，根据排名将英雄插入到指定位置
  	//(如果有这个排名，则添加失败，并给出提示)
  	public void addByOrder(HeroNode heroNode) {
  		//因为头节点不能动，因此我们仍然通过一个辅助指针(变量)来帮助找到添加的位置
  		//因为单链表，因为我们找的temp 是位于 添加位置的前一个节点，否则插入不了
  		HeroNode temp = head;
  		boolean flag = false; // flag标志添加的编号是否存在，默认为false
  		while(true) {
  			if(temp.next == null) {//说明temp已经在链表的最后
  				break; //
  			} 
  			if(temp.next.no > heroNode.no) { //位置找到，就在temp的后面插入
  				break;
  			} else if (temp.next.no == heroNode.no) {//说明希望添加的heroNode的编号已然存在
  				
  				flag = true; //说明编号存在
  				break;
  			}
  			temp = temp.next; //后移，遍历当前链表
  		}
  		//判断flag 的值
  		if(flag) { //不能添加，说明编号存在
  			System.out.printf("准备插入的英雄的编号 %d 已经存在了, 不能加入\n", heroNode.no);
  		} else {
  			//插入到链表中, temp的后面
  			heroNode.next = temp.next;
  			temp.next = heroNode;
  		}
  	}
  
  	//修改节点的信息, 根据no编号来修改，即no编号不能改.
  	//说明
  	//1. 根据 newHeroNode 的 no 来修改即可
  	public void update(HeroNode newHeroNode) {
  		//判断是否空
  		if(head.next == null) {
  			System.out.println("链表为空~");
  			return;
  		}
  		//找到需要修改的节点, 根据no编号
  		//定义一个辅助变量
  		HeroNode temp = head.next;
  		boolean flag = false; //表示是否找到该节点
  		while(true) {
  			if (temp == null) {
  				break; //已经遍历完链表
  			}
  			if(temp.no == newHeroNode.no) {
  				//找到
  				flag = true;
  				break;
  			}
  			temp = temp.next;
  		}
  		//根据flag 判断是否找到要修改的节点
  		if(flag) {
  			temp.name = newHeroNode.name;
  			temp.nickname = newHeroNode.nickname;
  		} else { //没有找到
  			System.out.printf("没有找到 编号 %d 的节点，不能修改\n", newHeroNode.no);
  		}
  	}
  	
  	//删除节点
  	//思路
  	//1. head 不能动，因此我们需要一个temp辅助节点找到待删除节点的前一个节点
  	//2. 说明我们在比较时，是temp.next.no 和  需要删除的节点的no比较
  	public void del(int no) {
  		HeroNode temp = head;
  		boolean flag = false; // 标志是否找到待删除节点的
  		while(true) {
  			if(temp.next == null) { //已经到链表的最后
  				break;
  			}
  			if(temp.next.no == no) {
  				//找到的待删除节点的前一个节点temp
  				flag = true;
  				break;
  			}
  			temp = temp.next; //temp后移，遍历
  		}
  		//判断flag
  		if(flag) { //找到
  			//可以删除
  			temp.next = temp.next.next;
  		}else {
  			System.out.printf("要删除的 %d 节点不存在\n", no);
  		}
  	}
  	
  	//显示链表[遍历]
  	public void list() {
  		//判断链表是否为空
  		if(head.next == null) {
  			System.out.println("链表为空");
  			return;
  		}
  		//因为头节点，不能动，因此我们需要一个辅助变量来遍历
  		HeroNode temp = head.next;
  		while(true) {
  			//判断是否到链表最后
  			if(temp == null) {
  				break;
  			}
  			//输出节点的信息
  			System.out.println(temp);
  			//将temp后移， 一定小心
  			temp = temp.next;
  		}
  	}
  }
  
  //定义HeroNode ， 每个HeroNode 对象就是一个节点
  class HeroNode {
  	public int no;
  	public String name;
  	public String nickname;
  	public HeroNode next; //指向下一个节点
  	//构造器
  	public HeroNode(int no, String name, String nickname) {
  		this.no = no;
  		this.name = name;
  		this.nickname = nickname;
  	}
  	//为了显示方法，我们重新toString
  	@Override
  	public String toString() {
  		return "HeroNode [no=" + no + ", name=" + name + ", nickname=" + nickname + "]";
  	}
  	
  }
  

单链表面试题：
1、获取单链表节点个数（不含头节点）？

//param head 链表的头节点
//return 返回的就是有效节点的个数
	public static int getLength(HeroNode head) {
		if(head.next == null) { //空链表
			return 0;
		}
		int length = 0;
		//定义一个辅助的变量, 这里我们没有统计头节点
		HeroNode cur = head.next;
		while(cur != null) {
			length++;
			cur = cur.next; //遍历
		}
		return length;
	}

2、查找单链？表中的倒数第k个结点 ？【新浪面试题】

	//1. 编写一个方法，接收head节点，同时接收一个index 
	//2. index 表示是倒数第index个节点
	//3. 先把链表从头到尾遍历，得到链表的总的长度 getLength
	//4. 得到size 后，我们从链表的第一个开始遍历 (size-index)个，就可以得到
	//5. 如果找到了，则返回该节点，否则返回nulll
	
public static HeroNode findLastIndexNode(HeroNode head, int index) {
		//判断如果链表为空，返回null
		if(head.next == null) {
			return null;//没有找到
		}
		//第一个遍历得到链表的长度(节点个数)
		int size = getLength(head);
		//第二次遍历  size-index 位置，就是我们倒数的第K个节点
		//先做一个index的校验
		if(index <=0 || index > size) {
			return null; 
		}
		//定义给辅助变量， for 循环定位到倒数的index
		HeroNode cur = head.next; //3 // 3 - 1 = 2
		for(int i =0; i< size - index; i++) {
			cur = cur.next;
		}
		return cur;
		
	}

3、链表反转？

//将单链表反转
	public static void reversetList(HeroNode head) {
		//如果当前链表为空，或者只有一个节点，无需反转，直接返回
		if(head.next == null || head.next.next == null) {
			return ;
		}
		
		//定义一个辅助的指针(变量)，帮助我们遍历原来的链表
		HeroNode cur = head.next;
		HeroNode next = null;// 指向当前节点[cur]的下一个节点
		HeroNode reverseHead = new HeroNode(0, "", "");

		//遍历原来的链表，每遍历一个节点，就将其取出，并放在新的链表reverseHead 的最前端
		while(cur != null) { 
			next = cur.next;//先暂时保存当前节点的下一个节点，因为后面需要使用
			cur.next = reverseHead.next;//将cur的下一个节点指向新的链表的最前端
			reverseHead.next = cur; //将cur 连接到新的链表上
			cur = next;//让cur后移
		}
		//将head.next 指向 reverseHead.next , 实现单链表的反转
		head.next = reverseHead.next;
	}

4、逆序打印链表？

//可以利用栈这个数据结构，将各个节点压入到栈中，然后利用栈的先进后出的特点，就实现了逆序打印的效果
	public static void reversePrint(HeroNode head) {
		if(head.next == null) {
			return;//空链表，不能打印
		}
		//创建要给一个栈，将各个节点压入栈
		Stack<HeroNode> stack = new Stack<HeroNode>();
		HeroNode cur = head.next;
		//将链表的所有节点压入栈
		while(cur != null) {
			stack.push(cur);
			cur = cur.next; //cur后移，这样就可以压入下一个节点
		}
		//将栈中的节点进行打印,pop 出栈
		while (stack.size() > 0) {
			System.out.println(stack.pop()); //stack的特点是先进后出
		}
	}

代码思路解释是按照韩顺平老师讲解来的，思路有但是自己写一遍还是写不出。。。Awkward！

 

 

----------------算法学习的过程

第一章：讨论算法？
    1-1 算法概述
第二章：排序基础
    2-1 选择排序法
    2-2 使用模板（泛型）编写算法
    2-3 随机生成算法测试用例
    2-4 测试算法的性能
    2-5 插入排序法
    2-6 插入排序法的改进
    2-7 更多关于O（n*2）排序算法的思考
第三章：高级排序问题
    3-1 归并排序法
    3-2 归并排序法的实现
    3-3 归并排序法的优化
    3-4 自底向上的归并排序算法
    3-5 快速排序法
    3-6 随机化快速排序法
    3-7 双路快速排序法
    3-8 三路快速排序法
    3-9 归并排序和快速排序的衍生问题
第四章：堆和堆排序
    4-1 为什么使用堆
    4-2 堆的基本存储
    4-3 Shift Up
    4-4 Shift Down
    4-5 基础堆排序和Heapify
    4-6 优化的堆排序
    4-7 排序算法总结
    4-8 索引堆
    4-9 索引堆的优化
    4-10 和堆相关的其他问题
第五章：二分搜索树
    5-1 二分查找法
    5-2 二分搜索树基础
    5-3 二分搜索树的节点插入
    5-4 二分搜索书的查找
    5-5 二分搜索树的遍历（深度优先遍历）
    5-6 层序遍历（广度优先遍历）
    5-7 删除最大值，最小值
    5-8 二分搜索树的删除
    5-9 二分搜索树的顺序性
    5-10 二分搜索树的局限性
    5-11 树形问题和更多树。
第六章:并查集
    6-1 并查集基础
    6-2 Qucik Find
    6-3 Quick Union
    6-4 基于size的优化
    6-5 基于rank的优化
    6-6 路径压缩
第七章: 
    7-1 图论基础
    7-2 图的表示
    7-3 相邻点迭代器
    7-4 图的算法框架
    7-5 深度优先遍历和联通分量
    7-6 寻路
    7-7 广度优先遍历和最短路径
    7-8 迷宫生成，ps抠图--更多无权图的应用
第八章：最小生成树
    8-1 有权图
    8-2 最小生成树问题和切分定理
    8-3 Prim算法的第一个实现
    8-4 Prim算法的优化
    8-5 优化后的Prim算法的实现
    8-6 Krusk算法
    8-7 最小生成树算法的思考
第九章：最短路径
    9-1 最短路径问题和松弛操作
    9-2 Dijkstra算法的思想
    9-3 实现Dijkstra算法
    9-4 负权边和Bellman-Ford算法
    9-5 实现Bellman-Ford算法
    9-6 更多和最短路径相关的思考
第十章：结束语
    10-1 总结，算法思想！